
Space diagonal
Encyclopedia
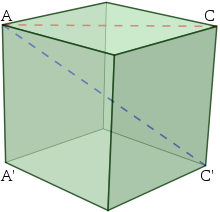
Cuboid
In geometry, a cuboid is a solid figure bounded by six faces, forming a convex polyhedron. There are two competing definitions of a cuboid in mathematical literature...
or a magic cube
Magic cube
In mathematics, a magic cube is the 3-dimensional equivalent of a magic square, that is, a number of integers arranged in a n x n x n pattern such that the sum of the numbers on each row, each column, each pillar and the four main space diagonals is equal to a single number, the so-called magic...
, the four space diagonals are the lines that go from a corner of the box or cube, through the center of the box or cube, to the opposite corner. These lines are also called triagonals or volume diagonals.
For the cube to be considered magic, these four lines must sum correctly.
The word triagonal is derived from the fact that as you travel down the line, three coordinates change. The equivalent in a square
Square (geometry)
In geometry, a square is a regular quadrilateral. This means that it has four equal sides and four equal angles...
is diagonal
Diagonal
A diagonal is a line joining two nonconsecutive vertices of a polygon or polyhedron. Informally, any sloping line is called diagonal. The word "diagonal" derives from the Greek διαγώνιος , from dia- and gonia ; it was used by both Strabo and Euclid to refer to a line connecting two vertices of a...
, because two coordinates change. In a tesseract
Tesseract
In geometry, the tesseract, also called an 8-cell or regular octachoron or cubic prism, is the four-dimensional analog of the cube. The tesseract is to the cube as the cube is to the square. Just as the surface of the cube consists of 6 square faces, the hypersurface of the tesseract consists of 8...
it is quadragonal because 4 coordinates change, etc.
The space diagonal of a cube
Cube
In geometry, a cube is a three-dimensional solid object bounded by six square faces, facets or sides, with three meeting at each vertex. The cube can also be called a regular hexahedron and is one of the five Platonic solids. It is a special kind of square prism, of rectangular parallelepiped and...
with side length a is
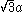 .
.r-agonals
This section applies particularly to Magic hypercubes.The magic hypercube community has started to recognize an abbreviated expression for these space diagonals. By using r as a variable to describe the various
agonals, a concise notation is possible.
If r =
- 2 then we have a diagonal. 2 coordinates change.
- 3 = a triagonal. 3 coordinates change
- 4 = a quadragonal. 4 coordinates change
- n = the dimension of the hypercube. These 2n-1 agonals are required to sum correctly for the hypercube to be considered magic.
...
By extension,
- 1 = the lines parallel to the faces. Only 1 coordinate changes. A 1-agonal may be called a monagonal, in keeping with a diagonal, a triagonal, etc. Lines parallel to the faces of the hypercube have, in the past, also been referred to as i-rows.
Because the prefix pan indicates all, we can concisely state the characteristics or a magic hypercube.
Post the formula for the number of space diagonals, as it is a necessary formula.
For example;
- If pan-r-agonals sum correctly for r = 1 and 2, we know our square is pandiagonal magic.
- If pan-r-agonals sum correctly for r = 1 and 3, we have a pantriagonal magic cube (the equivalent of a pandiagonal magic square).
- If the r-agonals sum correctly for r = 1 and n, then we know that the magic hypercube is simple magic regardless of what dimension it is!!
The length of an r-agonal of a hypercube
Hypercube
In geometry, a hypercube is an n-dimensional analogue of a square and a cube . It is a closed, compact, convex figure whose 1-skeleton consists of groups of opposite parallel line segments aligned in each of the space's dimensions, perpendicular to each other and of the same length.An...
with side length a is
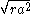 .
.
