
The fifty nine icosahedra
Encyclopedia
Harold Scott MacDonald Coxeter
Harold Scott MacDonald "Donald" Coxeter, was a British-born Canadian geometer. Coxeter is regarded as one of the great geometers of the 20th century. He was born in London but spent most of his life in Canada....
, P. Du Val
Patrick du Val
Patrick du Val was a British mathematician, known for his work on algebraic geometry, differential geometry, and general relativity. The concept of Du Val singularity of an algebraic surface is named after him....
, H. T. Flather and J. F. Petrie. It enumerates the stellation
Stellation
Stellation is a process of constructing new polygons , new polyhedra in three dimensions, or, in general, new polytopes in n dimensions. The process consists of extending elements such as edges or face planes, usually in a symmetrical way, until they meet each other again...
s of the regular convex or Platonic
Platonic solid
In geometry, a Platonic solid is a convex polyhedron that is regular, in the sense of a regular polygon. Specifically, the faces of a Platonic solid are congruent regular polygons, with the same number of faces meeting at each vertex; thus, all its edges are congruent, as are its vertices and...
icosahedron
Icosahedron
In geometry, an icosahedron is a regular polyhedron with 20 identical equilateral triangular faces, 30 edges and 12 vertices. It is one of the five Platonic solids....
, according to a set of rules put forward by J. C. P. Miller
J. C. P. Miller
Jeffrey Charles Percy Miller was an English mathematician and computing pioneer. He worked in number theory and on geometry, particularly polyhedra, where Miller's monster refers to the great dirhombicosidodecahedron....
. There can also be more stellations, including one with Chiral Tetrahedral symmetry known as "Tetrahedron minus Icosahedron".
The book was completely reset and the plates redrawn for the Third Edition, with additional reference material and photographs, by K. and D. Crennell.
Miller's rules
Although MillerJ. C. P. Miller
Jeffrey Charles Percy Miller was an English mathematician and computing pioneer. He worked in number theory and on geometry, particularly polyhedra, where Miller's monster refers to the great dirhombicosidodecahedron....
did not contribute to the book directly, he was a close colleague of Coxeter and Petrie. His contribution is immortalised in his set of rules for defining which stellation forms should be considered "properly significant and distinct":
- (i) The faces must lie in twenty planes, viz., the bounding planes of the regular icosahedron.
- (ii) All parts composing the faces must be the same in each plane, although they may be quite disconnected.
- (iii) The parts included in any one plane must have trigonal symmetry, without or with reflection. This secures icosahedral symmetry for the whole solid.
- (iv) The parts included in any plane must all be "accessible" in the completed solid (i.e. they must be on the "outside". In certain cases we should require models of enormous size in order to see all the outside. With a model of ordinary size, some parts of the "outside" could only be explored by a crawling insect).
- (v) We exclude from consideration cases where the parts can be divided into two sets, each giving a solid with as much symmetry as the whole figure. But we allow the combination of an enantiomorphous pair having no common part (which actually occurs in just one case).
Rules (i) to (iii) are symmetry requirements for the face planes. Rule (iv) excludes buried holes, to ensure that no two stellations look outwardly identical. Rule (v) prevents any disconnected compound of simpler stellations.
Coxeter
Coxeter was the main driving force behind the work. He carried out the original analysis based on Miller's rules, adopting a number of techniques such as combinatoricsCombinatorics
Combinatorics is a branch of mathematics concerning the study of finite or countable discrete structures. Aspects of combinatorics include counting the structures of a given kind and size , deciding when certain criteria can be met, and constructing and analyzing objects meeting the criteria ,...
and abstract graph theory
Graph theory
In mathematics and computer science, graph theory is the study of graphs, mathematical structures used to model pairwise relations between objects from a certain collection. A "graph" in this context refers to a collection of vertices or 'nodes' and a collection of edges that connect pairs of...
whose use in a geometrical context was then novel.
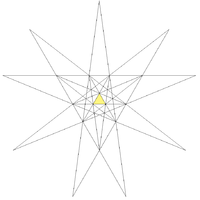
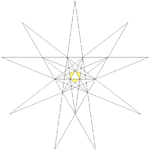
He observed that the stellation diagram comprised many line segments. He then developed procedures for manipulating combinations of the adjacent plane regions, to formally enumerate the combinations allowed under Miller's rules.
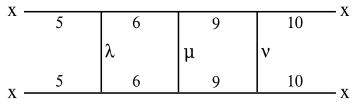
His graph, reproduced here, shows the connectivity of the various faces identified in the stellation diagram (see below). The Greek symbols represent sets of possible alternatives:
- λ may be 3 or 4
- μ may be 7 or 8
- ν may be 11 or 12
Du Val
Du Val devised a symbolic notation for identifying sets of congruent cells, based on the observation that they lie in "shells" around the original icosahedron. Based on this he tested all possible combinations against Miller's rules, confirming the result of Coxeter's more analytical approach.Flather
Flather's contribution was indirect: he made card models of all 59. When he first met Coxeter he had already made many stellations, including some "non-Miller" examples. He went on to complete the series of fifty-nine, which are preserved in the mathematics library of Cambridge University, England. The library also holds some non-Miller models, but it is not known whether these were made by Flather or by Miller's later students.Petrie
John Flinders Petrie was a lifelong friend of Coxeter and had a remarkable ability to visualise four-dimensional geometry. He and Coxeter had worked together on many mathematical problems. His direct contribution to the fifty nine icosahedra was the exquisite set of three-dimensional drawings which provide much of the fascination of the published work.The Crennells
For the Third Edition, Kate and David Crennell completely reset the text and redrew the illustrations and Plates. They also added a reference section containing tables, diagrams, and photographs of some of the Cambridge models (which at that time were all thought to be Flather's). It includes an index of all 59, numbered sequentially as they appear in the book. A few errors crept into the editing process, such as in some of the Plates and in the annotations to Fig.7. A PDF file of corrected pages is available online.List of the fifty nine icosahedra
Before Coxeter, only Brückner and Wheeler had recorded any significant sets of stellations, although a few such as the great icosahedron had been known for longer. Since publication of The 59, Wenninger published instructions on making models of some; his scheme has become widely referenced, although he only recorded a few stellations.Table of the fifty nine icosahedra
| Crennell | VRML VRML VRML is a standard file format for representing 3-dimensional interactive vector graphics, designed particularly with the World Wide Web in mind... | Cells | Faces | Wenninger | Wheeler | Brückner | Remarks | Face | 3D |
|---|---|---|---|---|---|
| 1 | http://www.georgehart.com/virtual-polyhedra/vrml/stellated_icosahedron_(1)_(5_color).wrl | A | 0 | 4 Icosahedron |
1 |
|The Platonic
Platonic solid
In geometry, a Platonic solid is a convex polyhedron that is regular, in the sense of a regular polygon. Specifically, the faces of a Platonic solid are congruent regular polygons, with the same number of faces meeting at each vertex; thus, all its edges are congruent, as are its vertices and...
icosahedron
Icosahedron
In geometry, an icosahedron is a regular polyhedron with 20 identical equilateral triangular faces, 30 edges and 12 vertices. It is one of the five Platonic solids....
|

|
|-
|2
|http://www.georgehart.com/virtual-polyhedra/vrml/stellated_icosahedron_(2)_(5_color).wrl
||B ||1 ||26
Triakis icosahedron
||2 ||
|First stellation of the icosahedron,
small triambic icosahedron
Small triambic icosahedron
In geometry, the small triambic icosahedron is the dual to the uniform small ditrigonal icosidodecahedron. It is composed of 20 intersecting isogonal hexagon faces. It has 60 edges and 32 vertices, and Euler characteristic of −8....
,
or Triakisicosahedron
|
|

|-
|3
|http://www.georgehart.com/virtual-polyhedra/vrml/stellated_icosahedron_(3)_(5_color).wrl
||C ||2 ||23
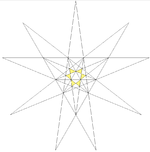
Compound of five octahedra ||3 ||
| Regular compound of five octahedra
Compound of five octahedra
This polyhedron can be seen as either a polyhedral stellation or a compound. This compound was first described by Edmund Hess in 1876.- As a stellation :It is the second stellation of the icosahedron, and given as Wenninger model index 23....
|
|

|-
|4
|http://www.georgehart.com/virtual-polyhedra/vrml/stellated_icosahedron_(4)_(5_color).wrl
||D ||3 4 || ||4 ||
|
|
|
|-
|5
|http://www.georgehart.com/virtual-polyhedra/vrml/stellated_icosahedron_(5)_(5_color).wrl
||E ||5 6 7 || || ||
|
|
|
|-
|6
|http://www.georgehart.com/virtual-polyhedra/vrml/stellated_icosahedron_(6)_(5_color).wrl
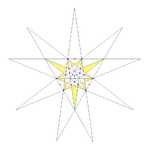
||F ||8 9 10 ||27
Second stellation ||19 ||
|
|
|

|-
|7
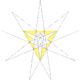
|http://www.georgehart.com/virtual-polyhedra/vrml/stellated_icosahedron_(7)_(5_color).wrl
||G ||11 12 ||41
Great icosahedron ||11 ||
| Great icosahedron
|
|

|-
|8
|http://www.georgehart.com/virtual-polyhedra/vrml/stellated_icosahedron_(8)_(5_color).wrl
||H ||13 ||42
Final stellation ||12 ||
| Final stellation of the icosahedron
Final stellation of the icosahedron
In geometry, the complete or final stellation of the icosahedron is the outermost stellation of the icosahedron, and is "complete" and "final" because it includes all of the cells in the icosahedron's stellation diagram....
or Echidnahedron
|

|

|-
|9
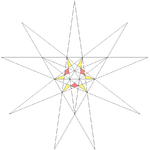
|http://www.georgehart.com/virtual-polyhedra/vrml/stellated_icosahedron_(9)_(5_color).wrl
||e1 ||3
Twelfth stellation || ||
|
|
|

|-
|10
|http://www.georgehart.com/virtual-polyhedra/vrml/stellated_icosahedron_(10)_(5_color).wrl
||f1 ||5
|
|
|
|-
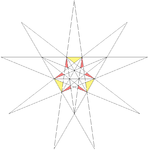
|11
|http://www.georgehart.com/virtual-polyhedra/vrml/stellated_icosahedron_(11)_(5_color).wrl
||g1 ||10
Fourth stellation ||21 ||
|
|
|

|-
|-
|12
|http://www.georgehart.com/virtual-polyhedra/vrml/stellated_icosahedron_(12)_(5_color).wrl
||e1f1 ||3
|-
|13
|http://www.georgehart.com/virtual-polyhedra/vrml/stellated_icosahedron_(13)_(5_color).wrl
||e1f1g1 ||3
|
|
|
|-
|14
|http://www.georgehart.com/virtual-polyhedra/vrml/stellated_icosahedron_(14)_(5_color).wrl
||f1g1 ||5
|-
|15
|http://www.georgehart.com/virtual-polyhedra/vrml/stellated_icosahedron_(15)_(5_color).wrl
||e2 ||4
|-
|16
|http://www.georgehart.com/virtual-polyhedra/vrml/stellated_icosahedron_(16)_(5_color).wrl
||f2||7
|
|
|
|-
|17
|http://www.georgehart.com/virtual-polyhedra/vrml/stellated_icosahedron_(17)_(5_color).wrl
||g2 ||8
|-
|18
|http://www.georgehart.com/virtual-polyhedra/vrml/stellated_icosahedron_(18)_(5_color).wrl
||e2f2 ||4
|-
|19
|http://www.georgehart.com/virtual-polyhedra/vrml/stellated_icosahedron_(19)_(5_color).wrl
||e2f2g2 ||4
|-
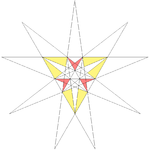
|20
|http://www.georgehart.com/virtual-polyhedra/vrml/stellated_icosahedron_(20)_(5_color).wrl
||f2g2 ||7
Fifth stellation || ||
|
|
|

|-
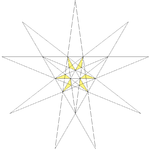
|21
|http://www.georgehart.com/virtual-polyhedra/vrml/stellated_icosahedron_(21)_(5_color).wrl
||De1 ||4 5 ||32
Seventh stellation ||10 ||
|
|
|

|-
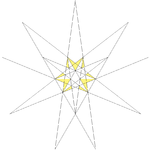
|22
|http://www.georgehart.com/virtual-polyhedra/vrml/stellated_icosahedron_(22)_(5_color).wrl
||Ef1 ||7 9 10 ||25
Compound of ten tetrahedra ||8 ||
| Regular compound of ten tetrahedra
Compound of ten tetrahedra
This polyhedron can be seen as either a polyhedral stellation or a compound. This compound was first described by Edmund Hess in 1876.- As a compound :It can also be seen as the compound of ten tetrahedra with full icosahedral symmetry...
|
|

|-
|23
|http://www.georgehart.com/virtual-polyhedra/vrml/stellated_icosahedron_(23)_(5_color).wrl
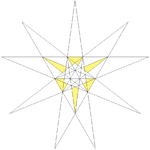
||Fg1 ||8 9 12 ||31
Sixth stellation ||17 ||
|
|
|

|-
|24
|http://www.georgehart.com/virtual-polyhedra/vrml/stellated_icosahedron_(24)_(5_color).wrl
||De1f1 ||4 6
|-
|25
|http://www.georgehart.com/virtual-polyhedra/vrml/stellated_icosahedron_(25)_(5_color).wrl
||De1f1g1 ||4 6
|-
|26
|http://www.georgehart.com/virtual-polyhedra/vrml/stellated_icosahedron_(26)_(5_color).wrl
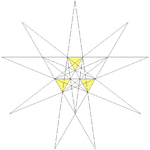
||Ef1g1 ||7 9 12 ||28
Third stellation ||9 ||
| Excavated dodecahedron
Excavated dodecahedron
In geometry, the excavated dodecahedron is a star polyhedron. Its exterior surface represents the Ef1g1 stellation of the icosahedron. Magnus Wenninger list it in his Polyhedran models book as model 28, and calls it the third stellation of icosahedron.It is also a facetting of the dodecahedron...
. Topologically a regular polyhedron
Regular polyhedron
A regular polyhedron is a polyhedron whose faces are congruent regular polygons which are assembled in the same way around each vertex. A regular polyhedron is highly symmetrical, being all of edge-transitive, vertex-transitive and face-transitive - i.e. it is transitive on its flags...
; see that article for more details.
|
|

|-
|27
|http://www.georgehart.com/virtual-polyhedra/vrml/stellated_icosahedron_(27)_(5_color).wrl
||De2 ||3 6 7 || ||5 ||
|
|
|
|-
|28
|http://www.georgehart.com/virtual-polyhedra/vrml/stellated_icosahedron_(28)_(5_color).wrl
||Ef2 ||5 6 8 || ||18 ||
|
|
|
|-
|29
|http://www.georgehart.com/virtual-polyhedra/vrml/stellated_icosahedron_(29)_(5_color).wrl
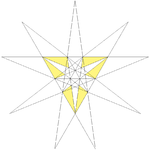
||Fg2 ||10 11 ||33
Eighth stellation ||14 ||
|
|
|

|-
|30
|http://www.georgehart.com/virtual-polyhedra/vrml/stellated_icosahedron_(30)_(5_color).wrl
||De2f2 ||3 6 8 ||34
Ninth stellation ||13 ||
|
|

|

|-
|31
|http://www.georgehart.com/virtual-polyhedra/vrml/stellated_icosahedron_(31)_(5_color).wrl
||De2f2g2 ||3 6 9
|-
|32
|http://www.georgehart.com/virtual-polyhedra/vrml/stellated_icosahedron_(32)_(5_color).wrl
||Ef2g2 ||5 6 9
|-
|33
|http://www.georgehart.com/virtual-polyhedra/vrml/stellated_icosahedron_(33)_(5_color).wrl
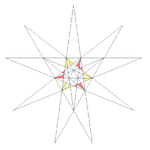
||f1 ||5
Tenth stellation || ||
|
|
|

|-
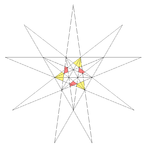
|34
|http://www.georgehart.com/virtual-polyhedra/vrml/stellated_icosahedron_(34)_(5_color).wrl
||e1f1 ||3
Eleventh stellation || ||
|
|
|

|-
|35
|http://www.georgehart.com/virtual-polyhedra/vrml/stellated_icosahedron_(35)_(5_color).wrl
||De1f1 ||4 5 6
|-
|36
|http://www.georgehart.com/virtual-polyhedra/vrml/stellated_icosahedron_(36)_(5_color).wrl
||f1g1 ||5
|-
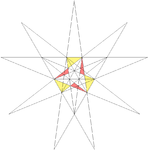
|37
|http://www.georgehart.com/virtual-polyhedra/vrml/stellated_icosahedron_(37)_(5_color).wrl
||e1f1g1 ||3
Fourteenth stellation || ||
|
|
|

|-
|38
|http://www.georgehart.com/virtual-polyhedra/vrml/stellated_icosahedron_(38)_(5_color).wrl
||De1f1g1 ||4 5 6
|-
|39
|http://www.georgehart.com/virtual-polyhedra/vrml/stellated_icosahedron_(39)_(5_color).wrl
||f1g2 ||5
|-
|40
|http://www.georgehart.com/virtual-polyhedra/vrml/stellated_icosahedron_(40)_(5_color).wrl
||e1f1g2 ||3
|-
|41
|http://www.georgehart.com/virtual-polyhedra/vrml/stellated_icosahedron_(41)_(5_color).wrl
||De1f1g2 ||4 5 6
|-
|42
|http://www.georgehart.com/virtual-polyhedra/vrml/stellated_icosahedron_(42)_(5_color).wrl
||f1f2g2 ||5
|-
|43
|http://www.georgehart.com/virtual-polyhedra/vrml/stellated_icosahedron_(43)_(5_color).wrl
||e1f1f2g2 ||3
|-
|44
|http://www.georgehart.com/virtual-polyhedra/vrml/stellated_icosahedron_(44)_(5_color).wrl
||De1f1f2g2 ||4 5 6
|-
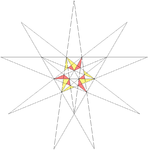
|45
|http://www.georgehart.com/virtual-polyhedra/vrml/stellated_icosahedron_(45)_(5_color).wrl
||e2f1 ||4
Fifteenth stellation || ||
|
|
|

|-
|46
|http://www.georgehart.com/virtual-polyhedra/vrml/stellated_icosahedron_(46)_(5_color).wrl
||De2f1 ||3 5
|-
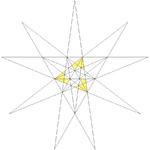
|47
|http://www.georgehart.com/virtual-polyhedra/vrml/stellated_icosahedron_(47)_(5_color).wrl
|Ef1
|5 6 7 9 10
|24
Compound of five tetrahedra
|7
(6: left handed)
|
|Regular Compound of five tetrahedra
Compound of five tetrahedra
This compound polyhedron is also a stellation of the regular icosahedron. It was first described by Edmund Hess in 1876.-As a compound:It can be constructed by arranging five tetrahedra in rotational icosahedral symmetry , as colored in the upper right model...
(right handed)
|
|

|-
|48
|http://www.georgehart.com/virtual-polyhedra/vrml/stellated_icosahedron_(48)_(5_color).wrl
|e2f1g1
|4
| || || || || ||
|-
|49
|http://www.georgehart.com/virtual-polyhedra/vrml/stellated_icosahedron_(49)_(5_color).wrl
|De2f1g1
|3 5
| || || || || ||
|-
|50
|http://www.georgehart.com/virtual-polyhedra/vrml/stellated_icosahedron_(50)_(5_color).wrl
|Ef1g1
|5 6 7 9 10
| || || || || ||
|-
|51
|http://www.georgehart.com/virtual-polyhedra/vrml/stellated_icosahedron_(51)_(5_color).wrl
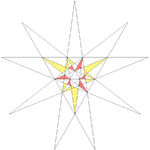
|e2f1f2
|4
|38
Thirteenth stellation || ||
|
|
|

|-
|52
|http://www.georgehart.com/virtual-polyhedra/vrml/stellated_icosahedron_(52)_(5_color).wrl
|De2f1f2
|3 5
| || || || || ||
|-
|53
|http://www.georgehart.com/virtual-polyhedra/vrml/stellated_icosahedron_(54)_(5_color).wrl
|Ef1f2
|5 6 8 9 10
| ||15
(16: left handed) || || || ||
|-
|54
|http://www.georgehart.com/virtual-polyhedra/vrml/stellated_icosahedron_(54)_(5_color).wrl
|e2f1f2g1
|4
| || || || || ||
|-
|55
|http://www.georgehart.com/virtual-polyhedra/vrml/stellated_icosahedron_(55)_(5_color).wrl
|De2f1f2g1
|3 5
| || || || || ||
|-
|56
|http://www.georgehart.com/virtual-polyhedra/vrml/stellated_icosahedron_(56)_(5_color).wrl
|Ef1f2g1
|5 6 8 9 10
| || || || || ||
|-
|57
|http://www.georgehart.com/virtual-polyhedra/vrml/stellated_icosahedron_(57)_(5_color).wrl
|e2f1f2g2
|4
| || || || || ||
|-
|58
|http://www.georgehart.com/virtual-polyhedra/vrml/stellated_icosahedron_(58)_(5_color).wrl
|De2f1f2g2
|3 5
| || || || || ||
|-
|59
|http://www.georgehart.com/virtual-polyhedra/vrml/stellated_icosahedron_(59)_(5_color).wrl
|Ef1f2g2
|5 6 9
| || || || || ||
|}
See also
- List of Wenninger polyhedron models – Wenninger's book Polyhedron models included 21 of these stellations.
- Solids with icosahedral symmetry

