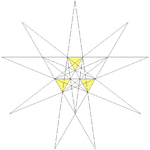
Excavated dodecahedron
Type	Stellation Stellation Stellation is a process of constructing new polygons , new polyhedra in three dimensions, or, in general, new polytopes in n dimensions. The process consists of extending elements such as edges or face planes, usually in a symmetrical way, until they meet each other again...
Index	W28, 26/59
Elements Euler characteristic In mathematics, and more specifically in algebraic topology and polyhedral combinatorics, the Euler characteristic is a topological invariant, a number that describes a topological space's shape or structure regardless of the way it is bent... (As a star polyhedron)	F = 20, E = 60 V = 20 (χ = −10)
Faces	Star hexagon
Vertex figure Vertex figure In geometry a vertex figure is, broadly speaking, the figure exposed when a corner of a polyhedron or polytope is sliced off.-Definitions - theme and variations:...	Concave hexagon
Symmetry group	icosahedral Icosahedral symmetry A regular icosahedron has 60 rotational symmetries, and a symmetry order of 120 including transformations that combine a reflection and a rotation...  (Ih)
Dual polyhedron Dual polyhedron In geometry, polyhedra are associated into pairs called duals, where the vertices of one correspond to the faces of the other. The dual of the dual is the original polyhedron. The dual of a polyhedron with equivalent vertices is one with equivalent faces, and of one with equivalent edges is another...	self
Stellation diagram Stellation diagram In geometry, a stellation diagram or stellation pattern is a two-dimensional diagram in the plane of some face of a polyhedron, showing lines where other face planes intersect with this one. The lines cause 2D space to be divided up into regions. Regions not intersected by any further lines are... Stellation Stellation Stellation is a process of constructing new polygons , new polyhedra in three dimensions, or, in general, new polytopes in n dimensions. The process consists of extending elements such as edges or face planes, usually in a symmetrical way, until they meet each other again...  core Convex hull Convex hull In mathematics, the convex hull or convex envelope for a set of points X in a real vector space V is the minimal convex set containing X.... Icosahedron Dodecahedron

In geometry

Geometry

Geometry arose as the field of knowledge dealing with spatial relationships. Geometry was one of the two fields of pre-modern mathematics, the other being the study of numbers ....

, the excavated dodecahedron is a star polyhedron

Star polyhedron

In geometry, a star polyhedron is a polyhedron which has some repetitive quality of nonconvexity giving it a star-like visual quality.There are two general kinds of star polyhedron:*Polyhedra which self-intersect in a repetitive way....

. Its exterior surface represents the Ef₁g₁

The fifty nine icosahedra

The Fifty Nine Icosahedra is a book written and illustrated by H. S. M. Coxeter, P. Du Val, H. T. Flather and J. F. Petrie. It enumerates the stellations of the regular convex or Platonic icosahedron, according to a set of rules put forward by J. C. P. Miller...

 stellation of the icosahedron. Magnus Wenninger

Magnus Wenninger

Father Magnus J. Wenninger OSB is a mathematician who works on constructing polyhedron models, and wrote the first book on their construction.-Early life and education:...

 list it in his Polyhedran models book as model 28, and calls it the third stellation of icosahedron.

It is also a facetting of the dodecahedron. When treated as a self-intersecting polyhedron, it is a noble polyhedron

Noble polyhedron

A noble polyhedron is one which is isohedral and isogonal . They were first studied in any depth by Hess and Bruckner around the turn of the century , and later by Grünbaum.-Classes of noble polyhedra:...

, having 20 star hexagons as faces. Although it is named the excavated dodecahedron, this is not strictly correct: a true excavated dodecahedron would have only the visible triangular faces instead of hexagonal ones.

The 20 vertices of the convex hull

Convex hull

In mathematics, the convex hull or convex envelope for a set of points X in a real vector space V is the minimal convex set containing X....

 match the vertex arrangement

Vertex arrangement

In geometry, a vertex arrangement is a set of points in space described by their relative positions. They can be described by their use in polytopes....

 of the dodecahedron.

Related polyhedra

The star hexagon face can be broken up into four equilateral triangles, three of which are the same size. A truly excavated dodecahedron would have the three congruent equilateral triangles as true faces of the polyhedron, while the interior equilateral triangle would be fully inside the polyhedron and would thus not be counted.

It is topologically equivalent to the {6, 6} hyperbolic tiling, by making the hexagons regular. As such, it is a regular polyhedron of index two: