This table contains an indexed list of the Uniform and stellated polyhedra from the book Polyhedron Models, by Magnus Wenninger

Magnus Wenninger

Father Magnus J. Wenninger OSB is a mathematician who works on constructing polyhedron models, and wrote the first book on their construction.-Early life and education:...

.

The book was written as a guide book to building polyhedra as physical models. It includes templates of face elements for construction and helpful hints in building, and also brief descriptions on the theory behind these shapes.

It contains the 75 nonprismatic uniform polyhedra

Uniform polyhedron

A uniform polyhedron is a polyhedron which has regular polygons as faces and is vertex-transitive...

, as well as 44 stellated forms

Stellation

Stellation is a process of constructing new polygons , new polyhedra in three dimensions, or, in general, new polytopes in n dimensions. The process consists of extending elements such as edges or face planes, usually in a symmetrical way, until they meet each other again...

 of the convex regular and semiregular polyhedra.

This list was written to honor this early polyhedral work from Wenninger, and to provide a detailed reference to the 119 numbered models in his book.

Models listed here can be cited as "Wenninger Model Number N", or W_N for brevity.

The polyhedra are grouped below in 5 tables: Regular (1–5), Semiregular (6–18), regular star polyhedra (20–22,41), Stellations and compounds (19–66), and uniform star polyhedra (67–119). The four regular star polyhedra are listed twice because they belong to both the uniform polyhedra and stellation groupings.

Platonic solids (regular) W1 to W5

Index	Name	Picture	Dual name	Dual picture	Wythoff symbol Wythoff symbol In geometry, the Wythoff symbol was first used by Coxeter, Longeut-Higgens and Miller in their enumeration of the uniform polyhedra. It represents a construction by way of Wythoff's construction applied to Schwarz triangles....	Vertex figure Vertex configuration In geometry, a vertex configuration is a short-hand notation for representing the vertex figure of a polyhedron or tiling as the sequence of faces around a vertex. For uniform polyhedra there is only one vertex type and therefore the vertex configuration fully defines the polyhedron... and Schläfli symbol	Symmetry group	U#	K#	V	E	F	Faces by type
1	Tetrahedron Tetrahedron In geometry, a tetrahedron is a polyhedron composed of four triangular faces, three of which meet at each vertex. A regular tetrahedron is one in which the four triangles are regular, or "equilateral", and is one of the Platonic solids...		Tetrahedron Tetrahedron In geometry, a tetrahedron is a polyhedron composed of four triangular faces, three of which meet at each vertex. A regular tetrahedron is one in which the four triangles are regular, or "equilateral", and is one of the Platonic solids...		3|2 3	{3,3}	Td	U01	K06	4	6	4	4{3}
2	Octahedron Octahedron In geometry, an octahedron is a polyhedron with eight faces. A regular octahedron is a Platonic solid composed of eight equilateral triangles, four of which meet at each vertex....		Hexahedron Hexahedron A hexahedron is any polyhedron with six faces, although usually implies the cube as a regular hexahedron with all its faces square, and three squares around each vertex....		4|2 3	{3,4}	Oh	U05	K10	6	12	8	8{3}
3	Hexahedron Hexahedron A hexahedron is any polyhedron with six faces, although usually implies the cube as a regular hexahedron with all its faces square, and three squares around each vertex....  (Cube)		Octahedron Octahedron In geometry, an octahedron is a polyhedron with eight faces. A regular octahedron is a Platonic solid composed of eight equilateral triangles, four of which meet at each vertex....		3|2 4	{4,3}	Oh	U06	K11	8	12	6	6{4}
4	Icosahedron Icosahedron In geometry, an icosahedron is a regular polyhedron with 20 identical equilateral triangular faces, 30 edges and 12 vertices. It is one of the five Platonic solids....		Dodecahedron		5|2 3	{3,5}	Ih	U22	K27	12	30	20	20{3}
5	Dodecahedron		Icosahedron Icosahedron In geometry, an icosahedron is a regular polyhedron with 20 identical equilateral triangular faces, 30 edges and 12 vertices. It is one of the five Platonic solids....		3|2 5	{5,3}	Ih	U23	K28	20	30	12	12{5}

Archimedean solids (Semiregular) W6 to W18

Index	Name	Picture	Dual name	Dual picture	Wythoff symbol Wythoff symbol In geometry, the Wythoff symbol was first used by Coxeter, Longeut-Higgens and Miller in their enumeration of the uniform polyhedra. It represents a construction by way of Wythoff's construction applied to Schwarz triangles....	Vertex figure Vertex configuration In geometry, a vertex configuration is a short-hand notation for representing the vertex figure of a polyhedron or tiling as the sequence of faces around a vertex. For uniform polyhedra there is only one vertex type and therefore the vertex configuration fully defines the polyhedron...	Symmetry group	U#	K#	V	E	F	Faces by type
6	Truncated tetrahedron Truncated tetrahedron In geometry, the truncated tetrahedron is an Archimedean solid. It has 4 regular hexagonal faces, 4 regular triangular faces, 12 vertices and 18 edges.- Area and volume :...		triakis tetrahedron Triakis tetrahedron In geometry, a triakis tetrahedron is an Archimedean dual solid, or a Catalan solid. Its dual is the truncated tetrahedron.It can be seen as a tetrahedron with triangular pyramids added to each face; that is, it is the Kleetope of the tetrahedron...		2 3|3	3.6.6	Td	U02	K07	12	18	8	4{3} + 4{6}
7	Truncated octahedron Truncated octahedron In geometry, the truncated octahedron is an Archimedean solid. It has 14 faces , 36 edges, and 24 vertices. Since each of its faces has point symmetry the truncated octahedron is a zonohedron....		tetrakis hexahedron Tetrakis hexahedron In geometry, a tetrakis hexahedron is a Catalan solid. Its dual is the truncated octahedron, an Archimedean solid. It can be seen as a cube with square pyramids covering each square face; that is, it is the Kleetope of the cube....		2 4|3	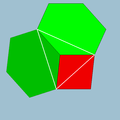4.6.6	Oh	U08	K13	24	36	14	6{4} + 8{6}
8	Truncated hexahedron Truncated cube In geometry, the truncated cube, or truncated hexahedron, is an Archimedean solid. It has 14 regular faces , 36 edges, and 24 vertices....		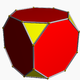triakis octahedron Triakis octahedron In geometry, a triakis octahedron is an Archimedean dual solid, or a Catalan solid. Its dual is the truncated cube.It can be seen as an octahedron with triangular pyramids added to each face; that is, it is the Kleetope of the octahedron. It is also sometimes called a trisoctahedron, or, more...		2 3|4	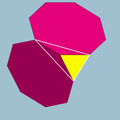3.8.8	Oh	U09	K14	24	36	14	8{3} + 6{8}
9	Truncated icosahedron Truncated icosahedron In geometry, the truncated icosahedron is an Archimedean solid, one of thirteen convex isogonal nonprismatic solids whose faces are two or more types of regular polygons.It has 12 regular pentagonal faces, 20 regular hexagonal faces, 60 vertices and 90 edges....		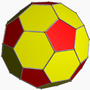pentakis dodecahedron Pentakis dodecahedron In geometry, a pentakis dodecahedron is a Catalan solid. Its dual is the truncated icosahedron, an Archimedean solid.It can be seen as a dodecahedron with a pentagonal pyramid covering each face; that is, it is the Kleetope of the dodecahedron...		2 5|3	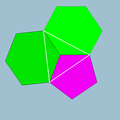5.6.6	Ih	U25	K30	60	90	32	12{5} + 20{6}
10	Truncated dodecahedron Truncated dodecahedron In geometry, the truncated dodecahedron is an Archimedean solid. It has 12 regular decagonal faces, 20 regular triangular faces, 60 vertices and 90 edges.- Geometric relations :...		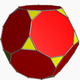triakis icosahedron Triakis icosahedron In geometry, the triakis icosahedron is an Archimedean dual solid, or a Catalan solid. Its dual is the truncated dodecahedron.It can be seen as an icosahedron with triangular pyramids augmented to each face; that is, it is the Kleetope of the icosahedron...		2 3|5	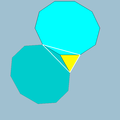3.10.10	Ih	U26	K31	60	90	32	20{3} + 12{10}
11	Cuboctahedron Cuboctahedron In geometry, a cuboctahedron is a polyhedron with eight triangular faces and six square faces. A cuboctahedron has 12 identical vertices, with two triangles and two squares meeting at each, and 24 identical edges, each separating a triangle from a square. As such it is a quasiregular polyhedron,...		rhombic dodecahedron Rhombic dodecahedron In geometry, the rhombic dodecahedron is a convex polyhedron with 12 rhombic faces. It is an Archimedean dual solid, or a Catalan solid. Its dual is the cuboctahedron.-Properties:...		2|3 4	3.4.3.4	Oh	U07	K12	12	24	14	8{3} + 6{4}
12	Icosidodecahedron Icosidodecahedron In geometry, an icosidodecahedron is a polyhedron with twenty triangular faces and twelve pentagonal faces. An icosidodecahedron has 30 identical vertices, with two triangles and two pentagons meeting at each, and 60 identical edges, each separating a triangle from a pentagon...		rhombic triacontahedron Rhombic triacontahedron In geometry, the rhombic triacontahedron is a convex polyhedron with 30 rhombic faces. It is an Archimedean dual solid, or a Catalan solid. It is the polyhedral dual of the icosidodecahedron, and it is a zonohedron....		2|3 5	3.5.3.5	Ih	U24	K29	30	60	32	20{3} + 12{5}
13	Small rhombicuboctahedron		deltoidal icositetrahedron Deltoidal icositetrahedron In geometry, a deltoidal icositetrahedron is a Catalan solid which looks a bit like an overinflated cube. Its dual polyhedron is the rhombicuboctahedron....		3 4|2	3.4.4.4	Oh	U10	K15	24	48	26	8{3}+(6+12){4}
14	Small rhombicosidodecahedron		deltoidal hexecontahedron Deltoidal hexecontahedron In geometry, a deltoidal hexecontahedron is a catalan solid which looks a bit like an overinflated dodecahedron. It is sometimes also called the trapezoidal hexecontahedron or strombic hexecontahedron...		3 5|2	3.4.5.4	Ih	U27	K32	60	120	62	20{3} + 30{4} + 12{5}
15	Great rhombicuboctahedron (Rhombitruncated cuboctahedron) (Truncated cuboctahedron)		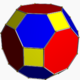disdyakis dodecahedron Disdyakis dodecahedron In geometry, a disdyakis dodecahedron, or hexakis octahedron, is a Catalan solid and the dual to the Archimedean truncated cuboctahedron. As such it is face-transitive but with irregular face polygons...		2 3 4|	4.6.8	Oh	U11	K16	48	72	26	12{4} + 8{6} + 6{8}
16	Great rhombicosidodecahedron (Rhombitruncated icosidodecahedron) (Truncated icosidodecahedron)		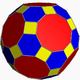disdyakis triacontahedron Disdyakis triacontahedron In geometry, a disdyakis triacontahedron, or hexakis icosahedron is a Catalan solid and the dual to the Archimedean truncated icosidodecahedron. As such it is face uniform but with irregular face polygons...		2 3 5|	4.6.10	Ih	U28	K33	120	180	62	30{4} + 20{6} + 12{10}
17	Snub cube Snub cube In geometry, the snub cube, or snub cuboctahedron, is an Archimedean solid.The snub cube has 38 faces, 6 of which are squares and the other 32 are equilateral triangles. It has 60 edges and 24 vertices. It is a chiral polyhedron, that is, it has two distinct forms, which are mirror images of each...		pentagonal icositetrahedron Pentagonal icositetrahedron In geometry, a pentagonal icositetrahedron is a Catalan solid which is the dual of the snub cube. It has two distinct forms, which are mirror images of each other....		|2 3 4	3.3.3.3.4	O	U12	K17	24	60	38	(8 + 24){3} + 6{4}
18	Snub dodecahedron Snub dodecahedron In geometry, the snub dodecahedron, or snub icosidodecahedron, is an Archimedean solid, one of thirteen convex isogonal nonprismatic solids constructed by two or more types of regular polygon faces....		pentagonal hexecontahedron Pentagonal hexecontahedron In geometry, a pentagonal hexecontahedron is a Catalan solid, dual of the snub dodecahedron. It has two distinct forms, which are mirror images of each other. It is also well-known to be the Catalan Solid with the most vertices...		|2 3 5	3.3.3.3.5	I	U29	K34	60	150	92	(20 + 60){3} + 12{5}

Kepler–Poinsot polyhedra (Regular star polyhedra

Star polyhedron

In geometry, a star polyhedron is a polyhedron which has some repetitive quality of nonconvexity giving it a star-like visual quality.There are two general kinds of star polyhedron:*Polyhedra which self-intersect in a repetitive way....

) W20, W21, W22 and W41

Index	Name	Picture	Dual name	Dual picture	Wythoff symbol Wythoff symbol In geometry, the Wythoff symbol was first used by Coxeter, Longeut-Higgens and Miller in their enumeration of the uniform polyhedra. It represents a construction by way of Wythoff's construction applied to Schwarz triangles....	Vertex figure Vertex configuration In geometry, a vertex configuration is a short-hand notation for representing the vertex figure of a polyhedron or tiling as the sequence of faces around a vertex. For uniform polyhedra there is only one vertex type and therefore the vertex configuration fully defines the polyhedron... and Schläfli symbol	Symmetry group	U#	K#	V	E	F	Faces by type
20	Small stellated dodecahedron		Great dodecahedron		5|25/2	{5/2,5}	Ih	U34	K39	12	30	12	12{5/2}
21	Great dodecahedron		Small stellated dodecahedron		5/2|2 5	{5,5/2}	Ih	U35	K40	12	30	12	12{5}
22	Great stellated dodecahedron		Great icosahedron		3|25/2	{5/2,3}	Ih	U52	K57	20	30	12	12{5/2}
41	Great icosahedron (16th stellation of icosahedron)		Great stellated dodecahedron		5/2|2 3	{3,5/2}	Ih	U53	K58	12	30	20	20{3}

Stellations of octahedron

Index	Name	Symmetry group	Picture	Facets
2	Octahedron Octahedron In geometry, an octahedron is a polyhedron with eight faces. A regular octahedron is a Platonic solid composed of eight equilateral triangles, four of which meet at each vertex.... (regular)	Oh
19	Stellated octahedron (Compound of two tetrahedra)	Oh

Stellations of dodecahedron

Index	Name	Symmetry group	Picture	Facets
5	Dodecahedron (regular)	Ih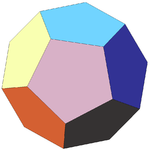
20	Small stellated dodecahedron (regular) (First stellation of dodecahedron)	Ih
21	Great dodecahedron (regular) (Second stellation of dodecahedron)	Ih
22	Great stellated dodecahedron (regular) (Third stellation of dodecahedron)	Ih

Stellations of icosahedron

Index	Name	Symmetry group	Picture	Facets
4	Icosahedron Icosahedron In geometry, an icosahedron is a regular polyhedron with 20 identical equilateral triangular faces, 30 edges and 12 vertices. It is one of the five Platonic solids....  (regular)	Ih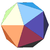
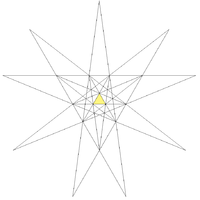26	First stellation of icosahedron Small triambic icosahedron Small triambic icosahedron In geometry, the small triambic icosahedron is the dual to the uniform small ditrigonal icosidodecahedron. It is composed of 20 intersecting isogonal hexagon faces. It has 60 edges and 32 vertices, and Euler characteristic of −8.... (Triakis icosahedron)	Ih
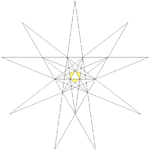23	Compound of five octahedra Compound of five octahedra This polyhedron can be seen as either a polyhedral stellation or a compound. This compound was first described by Edmund Hess in 1876.- As a stellation :It is the second stellation of the icosahedron, and given as Wenninger model index 23.... (First compound stellation of icosahedron)	Ih
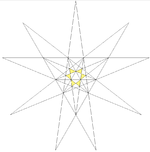24	Compound of five tetrahedra Compound of five tetrahedra This compound polyhedron is also a stellation of the regular icosahedron. It was first described by Edmund Hess in 1876.-As a compound:It can be constructed by arranging five tetrahedra in rotational icosahedral symmetry , as colored in the upper right model... (Second compound stellation of icosahedron)	I
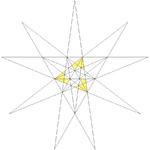25	Compound of ten tetrahedra Compound of ten tetrahedra This polyhedron can be seen as either a polyhedral stellation or a compound. This compound was first described by Edmund Hess in 1876.- As a compound :It can also be seen as the compound of ten tetrahedra with full icosahedral symmetry... (Third compound stellation of icosahedron)	Ih
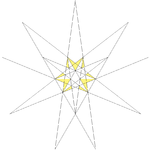27	Second stellation of icosahedron	Ih
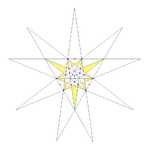28	Third stellation of icosahedron	Ih
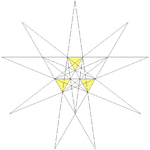29	Fourth stellation of icosahedron	Ih
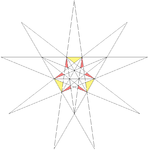30	Fifth stellation of icosahedron	Ih
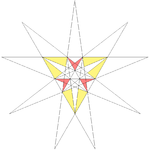31	Sixth stellation of icosahedron	Ih
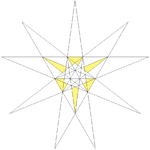32	Seventh stellation of icosahedron	Ih
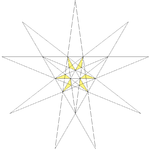33	Eighth stellation of icosahedron	Ih
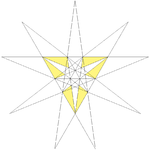34	Ninth stellation of icosahedron Great triambic icosahedron Great triambic icosahedron In geometry, the great triambic icosahedron and medial triambic icosahedron are visually identical dual uniform polyhedra. The exterior surface also represents the De1f1 stellation of the icosahedron. The only way to differentiate these two polyhedra is to mark which intersections between edges are...	Ih
35	Tenth stellation of icosahedron	I
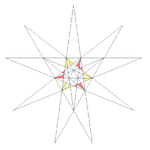36	Eleventh stellation of icosahedron	I
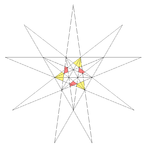37	Twelfth stellation of icosahedron	Ih
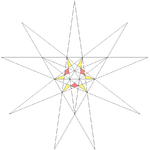38	Thirteenth stellation of icosahedron	I
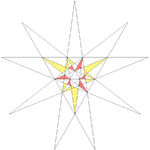39	Fourteenth stellation of icosahedron	I
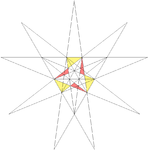40	Fifteenth stellation of icosahedron	I
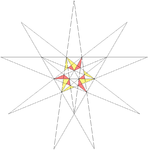41	Great icosahedron (regular) (Sixteenth stellation of icosahedron)	Ih
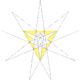42	Final stellation of the icosahedron Final stellation of the icosahedron In geometry, the complete or final stellation of the icosahedron is the outermost stellation of the icosahedron, and is "complete" and "final" because it includes all of the cells in the icosahedron's stellation diagram....	Ih

Stellations of cuboctahedron

Index	Name	Symmetry group	Picture	Facets (octahedral planes)	Facets (cube planes)
11	Cuboctahedron Cuboctahedron In geometry, a cuboctahedron is a polyhedron with eight triangular faces and six square faces. A cuboctahedron has 12 identical vertices, with two triangles and two squares meeting at each, and 24 identical edges, each separating a triangle from a square. As such it is a quasiregular polyhedron,...  (regular)	Oh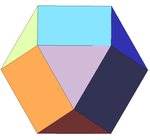
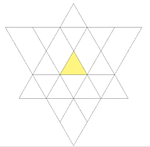43	Compound of cube and octahedron Compound of cube and octahedron This polyhedron can be seen as either a polyhedral stellation or a compound.- As a compound :It can be seen as the compound of an octahedron and a cube... (First stellation of cuboctahedron)	Oh
44	Second stellation of cuboctahedron	Oh
45	Third stellation of cuboctahedron	Oh
46	Fourth stellation of cuboctahedron	Oh

Stellations of icosidodecahedron

Index	Name	Symmetry group	Picture	Facets (icosahedral planes)	Facets (dodecahedral planes)
12	Icosidodecahedron Icosidodecahedron In geometry, an icosidodecahedron is a polyhedron with twenty triangular faces and twelve pentagonal faces. An icosidodecahedron has 30 identical vertices, with two triangles and two pentagons meeting at each, and 60 identical edges, each separating a triangle from a pentagon... (regular)	Ih
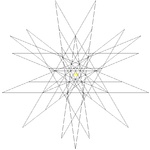47	(First stellation of icosidodecahedron) Compound of dodecahedron and icosahedron Compound of dodecahedron and icosahedron In geometry, this polyhedron can be seen as either a polyhedral stellation or a compound.- As a compound :It can be seen as the compound of an icosahedron and dodecahedron...	Ih
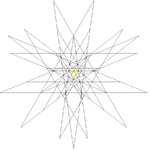48	Second stellation of icosidodecahedron	Ih
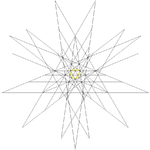49	Third stellation of icosidodecahedron	Ih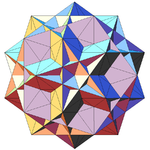
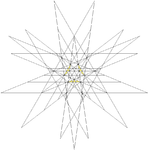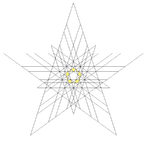50	Fourth stellation of icosidodecahedron (Compound of small stellated dodecahedron and triakis icosahedron)	Ih
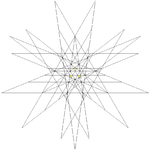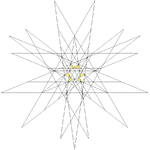
51	Fifth stellation of icosidodecahedron (Compound of small stellated dodecahedron and five octahedra)	Ih
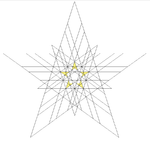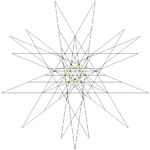
52	Sixth stellation of icosidodecahedron	Ih
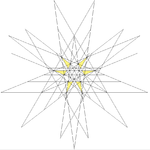
53	Seventh stellation of icosidodecahedron	Ih
54	Eighth stellation of icosidodecahedron (Compound of five tetrahedra and great dodecahedron)	I
55	Ninth stellation of icosidodecahedron	Ih
56	Tenth stellation of icosidodecahedron	Ih
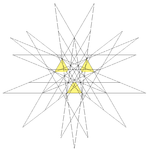57	Eleventh stellation of icosidodecahedron	Ih
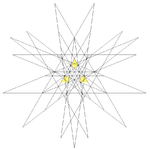58	Twelfth stellation of icosidodecahedron	Ih
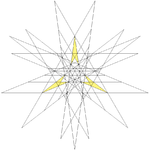
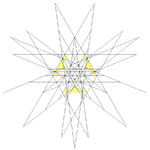59	Thirteenth stellation of icosidodecahedron	Ih
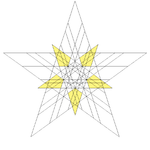60	Fourteenth stellation of icosidodecahedron	Ih
61	Compound of great stellated dodecahedron and great icosahedron	Ih
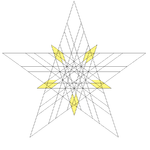62	Fifteenth stellation of icosidodecahedron	Ih
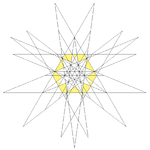63	Sixteenth stellation of icosidodecahedron	Ih
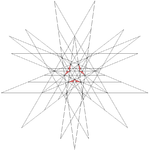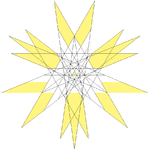
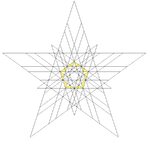64	Seventeenth stellation of icosidodecahedron	Ih
65	Eighteenth stellation of icosidodecahedron	Ih
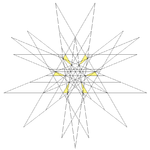
66	Nineteenth stellation of icosidodecahedron	Ih

Uniform nonconvex solids W67 to W119

Index	Name	Picture	Dual name	Dual picture	Wythoff symbol Wythoff symbol In geometry, the Wythoff symbol was first used by Coxeter, Longeut-Higgens and Miller in their enumeration of the uniform polyhedra. It represents a construction by way of Wythoff's construction applied to Schwarz triangles....	Vertex figure Vertex figure In geometry a vertex figure is, broadly speaking, the figure exposed when a corner of a polyhedron or polytope is sliced off.-Definitions - theme and variations:...	Symmetry group	U#	K#	V	E	F	Faces by type
67	Tetrahemihexahedron Tetrahemihexahedron In geometry, the tetrahemihexahedron or hemicuboctahedron is a uniform star polyhedron, indexed as U4. It has 6 vertices and 12 edges, and 7 faces: 4 triangular and 3 square. Its vertex figure is a crossed quadrilateral. It has Coxeter-Dynkin diagram of ....		Tetrahemihexacron Tetrahemihexacron In geometry, the tetrahemihexacron is the dual of the tetrahemihexahedron, and is one of nine dual hemipolyhedra.Since the tetrahemihexahedron has three square faces passing through the model centre, the tetrahemihexacron has three vertices at infinity...		3/23|2	4.3/2.4.3	Td	U04	K09	6	12	7	4{3}+3{4}
68	Octahemioctahedron Octahemioctahedron In geometry, the octahemioctahedron is a nonconvex uniform polyhedron, indexed as U3. Its vertex figure is a crossed quadrilateral.It is one of nine hemipolyhedra with 4 hexagonal faces passing through the model center.- Related polyhedra :...		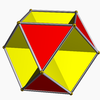Octahemioctacron Octahemioctacron In geometry, the octahemioctacron is the dual of the octahemioctahedron, and is one of nine dual hemipolyhedra. It appears visually indistinct from the hexahemioctacron....		3/23|3	6.3/2.6.3	Oh	U03	K08	12	24	12	8{3}+4{6}
69	Small cubicuboctahedron Small cubicuboctahedron In geometry, the small cubicuboctahedron is a uniform star polyhedron, indexed as U13. It has 20 faces , 48 edges, and 24 vertices. Its vertex figure is a crossed quadrilateral.- Related polyhedra :...		Small hexacronic icositetrahedron Small hexacronic icositetrahedron In geometry, the small hexacronic icositetrahedron is the dual of the small cubicuboctahedron....		3/24|4	8.3/2.8.4	Oh	U13	K18	24	48	20	8{3}+6{4}+6{8}
70	Small ditrigonal icosidodecahedron Small ditrigonal icosidodecahedron In geometry, the small ditrigonal icosidodecahedron is a nonconvex uniform polyhedron, indexed as U30.-Related polyhedra:Its convex hull is a regular dodecahedron...		Small triambic icosahedron Small triambic icosahedron In geometry, the small triambic icosahedron is the dual to the uniform small ditrigonal icosidodecahedron. It is composed of 20 intersecting isogonal hexagon faces. It has 60 edges and 32 vertices, and Euler characteristic of −8....		3|5/23	(5/2.3)3	Ih	U30	K35	20	60	32	20{3}+12{5/2}
71	Small icosicosidodecahedron Small icosicosidodecahedron In geometry, the small icosicosidodecahedron is a nonconvex uniform polyhedron, indexed as U31.- Related polyhedra :It shares its vertex arrangement with the great stellated truncated dodecahedron...		Small icosacronic hexecontahedron Small icosacronic hexecontahedron In geometry, the small icosacronic hexecontahedron is a nonconvex isohedral polyhedron. It is the dual of the uniform small icosicosidodecahedron. A Hexacontahedron has 60 faces....		5/23|3	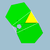6.5/2.6.3	Ih	U31	K36	60	120	52	20{3}+12{5/2}+20{6}
72	Small dodecicosidodecahedron Small dodecicosidodecahedron In geometry, the small dodecicosidodecahedron is a nonconvex uniform polyhedron, indexed as U33. Its vertex figure is a crossed quadrilateral.-Related polyhedra:...		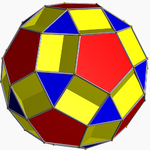Small dodecacronic hexecontahedron Small dodecacronic hexecontahedron In geometry, the small dodecacronic hexecontahedron is the dual of the small dodecicosidodecahedron.-External links:...		3/25|5	10.3/2.10.5	Ih	U33	K38	60	120	44	20{3}+12{5}+12{10}
73	Dodecadodecahedron		Medial rhombic triacontahedron Medial rhombic triacontahedron In geometry, the medial rhombic triacontahedron is a nonconvex isohedral polyhedron. It is the dual of the dodecadodecahedron. It has 30 intersecting rhombic faces.It can also be called the small stellated triacontahedron....		2|5/25	(5/2.5)2	Ih	U36	K41	30	60	24	12{5}+12{5/2}
74	Small rhombidodecahedron Small rhombidodecahedron In geometry, the small rhombidodecahedron is a nonconvex uniform polyhedron, indexed as U39. Its vertex figure is a crossed quadrilateral.- Related polyhedra :...		Small rhombidodecacron Small rhombidodecacron In geometry, the small rhombidodecacron is a nonconvex isohedral polyhedron. It is the dual of the small rhombidodecahedron. It has 60 intersecting antiparallelogram faces.- External links :*...		25/25|	10.4.10/9.4/3	Ih	U39	K44	60	120	42	30{4}+12{10}
75	Truncated great dodecahedron		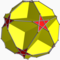Small stellapentakis dodecahedron Small stellapentakis dodecahedron In geometry, the small stellapentakis dodecahedron is a nonconvex isohedral polyhedron. It is the dual of the truncated great dodecahedron. It has 60 intersecting triangular faces.- External links :*...		25/2|5	10.10.5/2	Ih	U37	K42	60	90	24	12{5/2}+12{10}
76	Rhombidodecadodecahedron		Medial deltoidal hexecontahedron Medial deltoidal hexecontahedron In geometry, the medial deltoidal hexecontahedron is a nonconvex isohedral polyhedron. It is the dual of the rhombidodecadodecahedron. It has 60 intersecting quadrilateral faces.- External links :*...		5/25|2	4.5/2.4.5	Ih	U38	K43	60	120	54	30{4}+12{5}+12{5/2}
77	Great cubicuboctahedron Great cubicuboctahedron In geometry, the great cubicuboctahedron is a nonconvex uniform polyhedron, indexed as U14.- Related polyhedra :It shares the vertex arrangement with the convex truncated cube and two other nonconvex uniform polyhedra...		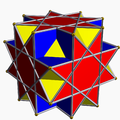Great hexacronic icositetrahedron Great hexacronic icositetrahedron In geometry, the great hexacronic icositetrahedron is the dual of the great cubicuboctahedron....		3 4|4/3	8/3.3.8/3.4	Oh	U14	K19	24	48	20	8{3}+6{4}+6{8/3}
78	Cubohemioctahedron Cubohemioctahedron In geometry, the cubohemioctahedron is a nonconvex uniform polyhedron, indexed as U15. Its vertex figure is a crossed quadrilateral.A nonconvex polyhedron has intersecting faces which do not represent new edges or faces...		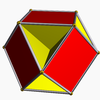Hexahemioctacron Hexahemioctacron In geometry, the hexahemioctacron is the dual of the cubohemioctahedron, and is one of nine dual hemipolyhedra. It appears visually indistinct from the octahemioctacron....		4/34|3	6.4/3.6.4	Oh	U15	K20	12	24	10	6{4}+4{6}
79	Cubitruncated cuboctahedron Cubitruncated cuboctahedron In geometry, the cubitruncated cuboctahedron is a nonconvex uniform polyhedron, indexed as U16.- Convex hull :Its convex hull is a nonuniform truncated cuboctahedron.- Cartesian coordinates :... (Cuboctatruncated cuboctahedron)		Tetradyakis hexahedron Tetradyakis hexahedron In geometry, the tetradyakis hexahedron is a nonconvex isohedral polyhedron. It has 48 intersecting scalene triangle faces, 72 edges, and 20 vertices.It is the dual of the uniform cubitruncated cuboctahedron.-External links:*...		4/33 4|	8/3.6.8	Oh	U16	K21	48	72	20	8{6}+6{8}+6{8/3}
80	Ditrigonal dodecadodecahedron Ditrigonal dodecadodecahedron In geometry, the Ditrigonal dodecadodecahedron is a nonconvex uniform polyhedron, indexed as U41.- Related polyhedra :Its convex hull is a regular dodecahedron...		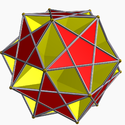Medial triambic icosahedron		3|5/35	(5/3.5)3	Ih	U41	K46	20	60	24	12{5}+12{5/2
81	Great ditrigonal dodecicosidodecahedron Great ditrigonal dodecicosidodecahedron In geometry, the great ditrigonal dodecicosidodecahedron is a nonconvex uniform polyhedron, indexed as U42.- Related polyhedra :It shares its vertex arrangement with the truncated dodecahedron...		Great ditrigonal dodecacronic hexecontahedron Great ditrigonal dodecacronic hexecontahedron In geometry, the great ditrigonal dodecacronic hexecontahedron is a nonconvex isohedral polyhedron. It is the dual of the uniform great ditrigonal dodecicosidodecahedron....		3 5|5/3	10/3.3.10/3.5	Ih	U42	K47	60	120	44	20{3}+12{5}+12{10/3}
82	Small ditrigonal dodecicosidodecahedron Small ditrigonal dodecicosidodecahedron In geometry, the small ditrigonal dodecicosidodecahedron is a nonconvex uniform polyhedron, indexed as U43. Its vertex figure is a crossed quadrilateral.- Related polyhedra :It shares its vertex arrangement with the great stellated truncated dodecahedron...		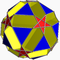Small ditrigonal dodecacronic hexecontahedron Small ditrigonal dodecacronic hexecontahedron In geometry, the small ditrigonal dodecacronic hexecontahedron is a nonconvex isohedral polyhedron. It is the dual of the uniform small ditrigonal dodecicosidodecahedron....		5/33|5	10.5/3.10.3	Ih	U43	K48	60	120	44	20{3}+12{5/2}+12{10}
83	Icosidodecadodecahedron Icosidodecadodecahedron In geometry, the icosidodecadodecahedron is a nonconvex uniform polyhedron, indexed as U44. Its vertex figure is a crossed quadrilateral.- Related polyhedra :It shares its vertex arrangement with the uniform compounds of 10 or 20 triangular prisms...		Medial icosacronic hexecontahedron Medial icosacronic hexecontahedron In geometry, the medial icosacronic hexecontahedron is a nonconvex isohedral polyhedron. It is the dual of the uniform icosidodecadodecahedron....		5/35|3	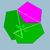6.5/3.6.5	Ih	U44	K49	60	120	44	12{5}+12{5/2}+20{6}
84	Icositruncated dodecadodecahedron Icositruncated dodecadodecahedron In geometry, the icositruncated dodecadodecahedron is a nonconvex uniform polyhedron, indexed as U45.- Convex hull :Its convex hull is a nonuniform great rhombicosidodecahedron.- Cartesian coordinates :... (Icosidodecatruncated icosidodecahedron)		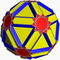Tridyakis icosahedron Tridyakis icosahedron In geometry, the tridyakis icosahedron is the dual polyhedron of the nonconvex uniform polyhedron, icositruncated dodecadodecahedron. It has 44 vertices, 180 edges, and 120 scalene triangular faces.-See also:* Catalan solid Duals to convex uniform polyhedra...		5/33 5|	10/3.6.10	Ih	U45	K50	120	180	44	20{6}+12{10}+12{10/3}
85	Nonconvex great rhombicuboctahedron (Quasirhombicuboctahedron)		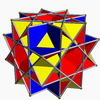Great deltoidal icositetrahedron Great deltoidal icositetrahedron In geometry, the great deltoidal icositetrahedron is the dual of the uniform great rhombicuboctahedron.-External links:...		3/24|2	4.3/2.4.4	Oh	U17	K22	24	48	26	8{3}+(6+12){4}
86	Small rhombihexahedron Small rhombihexahedron In geometry, the small rhombihexahedron is a nonconvex uniform polyhedron, indexed as U18. It has 18 faces , 48 edges, and 24 vertices. Its vertex figure is an antiparallelogram.-Related polyhedra:...		Small rhombihexacron Small rhombihexacron In geometry, the small rhombihexacron is the dual of the small rhombihexahedron. Its faces are antiparallelograms formed by pairs of coplanar triangles....		3/22 4|	4.8.4/3.8	Oh	U18	K23	24	48	18	12{4}+6{8}
87	Great ditrigonal icosidodecahedron		Great triambic icosahedron Great triambic icosahedron In geometry, the great triambic icosahedron and medial triambic icosahedron are visually identical dual uniform polyhedra. The exterior surface also represents the De1f1 stellation of the icosahedron. The only way to differentiate these two polyhedra is to mark which intersections between edges are...		3/2|3 5	(5.3.5.3.5.3)/2	Ih	U47	K52	20	60	32	20{3}+12{5}
88	Great icosicosidodecahedron Great icosicosidodecahedron In geometry, the great icosicosidodecahedron is a nonconvex uniform polyhedron, indexed as U48. Its vertex figure is a crossed quadrilateral.- Related polyhedra :It shares its vertex arrangement with the truncated dodecahedron...		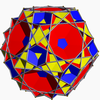Great icosacronic hexecontahedron Great icosacronic hexecontahedron In geometry, the great icosacronic hexecontahedron is the dual of the great icosicosidodecahedron.- External links :...		3/25|3	6.3/2.6.5	Ih	U48	K53	60	120	52	20{3}+12{5}+20{6}
89	Small icosihemidodecahedron Small icosihemidodecahedron In geometry, the small icosihemidodecahedron is a uniform star polyhedron, indexed as U49. Its vertex figure alternates two regular triangles and decagons as a crossed quadrilateral....		Small icosihemidodecacron Small icosihemidodecacron In geometry, the small icosihemidodecacron is the dual of the small icosihemidodecahedron, and is one of nine dual hemipolyhedra. It appears visually indistinct from the small dodecahemidodecacron....		3/23|5	10.3/2.10.3	Ih	U49	K54	30	60	26	20{3}+6{10}
90	Small dodecicosahedron Small dodecicosahedron In geometry, the small dodecicosahedron is a nonconvex uniform polyhedron, indexed as U50. Its vertex figure is a crossed quadrilateral.-Related polyhedra:It shares its vertex arrangement with the great stellated truncated dodecahedron...		Small dodecicosacron Small dodecicosacron In geometry, the small dodecicosacron is the dual of the small dodecicosahedron . It has 60 intersecting bow-tie-shaped faces.-External links:*...		3/23 5|	10.6.10/9.6/5	Ih	U50	K55	60	120	32	20{6}+12{10}
91	Small dodecahemidodecahedron Small dodecahemidodecahedron In geometry, the small dodecahemidodecahedron is a nonconvex uniform polyhedron, indexed as U51. Its vertex figure alternates two regular pentagons and decagons as a crossed quadrilateral....		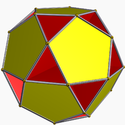Small dodecahemidodecacron Small dodecahemidodecacron In geometry, the small dodecahemidodecacron is the dual of the small dodecahemidodecahedron, and is one of nine dual hemipolyhedra. It appears visually indistinct from the small icosihemidodecacron....		5/45|5	10.5/4.10.5	Ih	U51	K56	30	60	18	12{5}+6{10}
92	Stellated truncated hexahedron (Quasitruncated hexahedron)		Great triakis octahedron Great triakis octahedron In geometry, the great triakis octahedron is the dual of the stellated truncated hexahedron . It has 24 intersecting isosceles triangle faces....		2 3|4/3	8/3.8/3.3	Oh	U19	K24	24	36	14	8{3}+6{8/3}
93	Great truncated cuboctahedron (Quasitruncated cuboctahedron)		Great disdyakis dodecahedron Great disdyakis dodecahedron In geometry, the great disdyakis dodecahedron is a nonconvex isohedral polyhedron. It is the dual of the uniform great truncated cuboctahedron....		4/32 3|	8/3.4.6	Oh	U20	K25	48	72	26	12{4}+8{6}+6{8/3}
94	Great icosidodecahedron		Great rhombic triacontahedron Great rhombic triacontahedron In geometry, the great rhombic triacontahedron is a nonconvex isohedral, isotoxal polyhedron. It is the dual of the great icosidodecahedron...		2|5/23	(5/2.3)2	Ih	U54	K59	30	60	32	20{3}+12{5/2}
95	Truncated great icosahedron		Great stellapentakis dodecahedron Great stellapentakis dodecahedron In geometry, the great stellapentakis dodecahedron is a nonconvex isohedral polyhedron. It is the dual of the truncated great icosahedron. It has 60 intersecting triangular faces.- External links :*...		25/2|3	6.6.5/2	Ih	U55	K60	60	90	32	12{5/2}+20{6}
96	Rhombicosahedron Rhombicosahedron In geometry, the rhombicosahedron is a nonconvex uniform polyhedron, indexed as U56. Its vertex figure is an antiparallelogram.- Related polyhedra :...		Rhombicosacron Rhombicosacron In geometry, the rhombicosacron is a nonconvex isohedral polyhedron. It is the dual of the uniform rhombicosahedron, U56. It has 50 vertices, 120 edges, and 60 crossed-quadrilateral faces.- External links :*...		25/23|	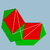6.4.6/5.4/3	Ih	U56	K61	60	120	50	30{4}+20{6}
97	Small stellated truncated dodecahedron (Quasitruncated small stellated dodecahedron)		Great pentakis dodecahedron Great pentakis dodecahedron In geometry, the great pentakis dodecahedron is a nonconvex isohedral polyhedron.It is the dual of the uniform small stellated truncated dodecahedron. The decagrammic faces pass close to the origin in the uniform polyhedron, causing this dual to be very spikey....		2 5|5/3	10/3.10/3.5	Ih	U58	K63	60	90	24	12{5}+12{10/3}
98	Truncated dodecadodecahedron (Quasitruncated dodecahedron)		Medial disdyakis triacontahedron Medial disdyakis triacontahedron In geometry, the medial disdyakis triacontahedron is a nonconvex isohedral polyhedron. It is the dual of the uniform truncated dodecadodecahedron....		5/32 5|	10/3.4.10	Ih	U59	K64	120	180	54	30{4}+12{10}+12{10/3}
99	Great dodecicosidodecahedron Great dodecicosidodecahedron In geometry, the great dodecicosidodecahedron is a nonconvex uniform polyhedron, indexed as U61.- Related polyhedra :It shares its vertex arrangement with the truncated great dodecahedron and the uniform compounds of 6 or 12 pentagonal prisms...		Great dodecacronic hexecontahedron Great dodecacronic hexecontahedron In geometry, the great dodecacronic hexecontahedron is a nonconvex isohedral polyhedron. It is the dual of the uniform great dodecicosidodecahedron....		5/23|5/3	10/3.5/2.10/3.3	Ih	U61	K66	60	120	44	20{3}+12{5/2}+12{10/3 }
100	Small dodecahemicosahedron Small dodecahemicosahedron In geometry, the small dodecahemicosahedron is a nonconvex uniform polyhedron, indexed as U62. Its vertex figure is a crossed quadrilateral.It is a hemipolyhedron with ten hexagonal faces passing through the model center.- Related polyhedra :...		Small dodecahemicosacron Small dodecahemicosacron In geometry, the small dodecahemicosacron is the dual of the small dodecahemicosahedron, and is one of nine dual hemipolyhedra. It appears visually indistinct from the great dodecahemicosacron....		5/35/2|3	6.5/3.6.5/2	Ih	U62	K67	30	60	22	12{5/2}+10{6}
101	Great dodecicosahedron Great dodecicosahedron In geometry, the great dodecicosahedron is a nonconvex uniform polyhedron, indexed as U63. Its vertex figure is a crossed quadrilateral.It has a composite Wythoff symbol, 3 5/3 |, requiring two different Schwarz triangles to generate it: and .Its vertex figure 6.10/3.6/5.10/7 is also ambiguous,...		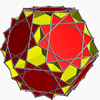Great dodecicosacron Great dodecicosacron In geometry, the great dodecicosacron is the dual of the great dodecicosahedron . It has 60 intersecting bow-tie-shaped faces.- External links :*...		5/35/23|	6.10/3.6/5.10/7	Ih	U63	K68	60	120	32	20{6}+12{10/3}
102	Great dodecahemicosahedron Great dodecahemicosahedron In geometry, the great dodecahemicosahedron is a nonconvex uniform polyhedron, indexed as U65. Its vertex figure is a crossed quadrilateral.It is a hemipolyhedron with ten hexagonal faces passing through the model center.- Related polyhedra :...		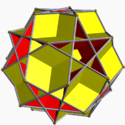Great dodecahemicosacron Great dodecahemicosacron In geometry, the great dodecahemicosacron is the dual of the great dodecahemicosahedron, and is one of nine dual hemipolyhedra. It appears visually indistinct from the small dodecahemicosacron....		5/45|3	6.5/4.6.5	Ih	U65	K70	30	60	22	12{5}+10{6}
103	Great rhombihexahedron Great rhombihexahedron In geometry, the great rhombihexahedron is a nonconvex uniform polyhedron, indexed as U21. Its dual is the great rhombihexacron. Its vertex figure is a crossed quadrilateral.- Related polyhedra :...		Great rhombihexacron Great rhombihexacron In geometry, the great rhombihexacron is a nonconvex isohedral polyhedron. It is the dual of the uniform great rhombihexahedron . It has 24 identical bow-tie-shaped faces, 18 vertices, and 48 edges....		4/33/22|	4.8/3.4/3.8/5	Oh	U21	K26	24	48	18	12{4}+6{8/3}
104	Great stellated truncated dodecahedron (Quasitruncated great stellated dodecahedron)		Great triakis icosahedron Great triakis icosahedron In geometry, the great triakis icosahedron is a nonconvex isohedral polyhedron. It is the dual of the uniform great stellated truncated dodecahedron....		2 3|5/3	10/3.10/3.3	Ih	U66	K71	60	90	32	20{3}+12{10/3}
105	Nonconvex great rhombicosidodecahedron (Quasirhombicosidodecahedron)		Great deltoidal hexecontahedron Great deltoidal hexecontahedron In geometry, the great deltoidal hexecontahedron is a nonconvex isohedral polyhedron. It is the dual of the nonconvex great rhombicosidodecahedron. It has 60 intersecting cross quadrilateral faces, 120 edges, and 62 vertices....		5/33|2	4.5/3.4.3	Ih	U67	K72	60	120	62	20{3}+30{4}+12{5/2}
106	Great icosihemidodecahedron Great icosihemidodecahedron In geometry, the great icosihemidodecahedron is a nonconvex uniform polyhedron, indexed as U71. Its vertex figure is a crossed quadrilateral.It is a hemipolyhedron with 6 decagrammic faces passing through the model center.- Related polyhedra :...		Great icosihemidodecacron Great icosihemidodecacron In geometry, the great icosihemidodecacron is the dual of the great icosihemidodecahedron, and is one of nine dual hemipolyhedra. It appears indistinct from the great dodecahemidodecacron....		3 3|5/3	10/3.3/2.10/3.3	Ih	U71	K76	30	60	26	20{3}+6{10/3}
107	Great dodecahemidodecahedron Great dodecahemidodecahedron In geometry, the great dodecahemidodecahedron is a nonconvex uniform polyhedron, indexed as U70. Its vertex figure is a crossed quadrilateral....		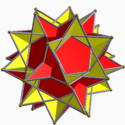Great dodecahemidodecacron Great dodecahemidodecacron In geometry, the great dodecahemidodecacron is the dual of the great dodecahemidodecahedron, and is one of nine dual hemipolyhedra. It is appears indistinct from the great icosihemidodecacron....		5/35/2|5/3	10/3.5/3.10/3.5/2	Ih	U70	K75	30	60	18	12{5/2}+6{10/3}
108	Great truncated icosidodecahedron (Great quasitruncated icosidodecahedron)		Great disdyakis triacontahedron Great disdyakis triacontahedron In geometry, the great disdyakis triacontahedron is a nonconvex isohedral polyhedron. It is the dual of the great truncated icosidodecahedron....		5/32 3|	10/3.4.6	Ih	U68	K73	120	180	62	30{4}+20{6}+12{10/3}
109	Great rhombidodecahedron Great rhombidodecahedron In geometry, the great rhombidodecahedron is a nonconvex uniform polyhedron, indexed as U73. Its vertex figure is a crossed quadrilateral.- Related polyhedra :...		Great rhombidodecacron Great rhombidodecacron In geometry, the great rhombidodecacron is a nonconvex isohedral polyhedron. It is the dual of the great rhombidodecahedron. Its faces are antiparallelograms....		3/25/32|	4.10/3.4/3.10/7	Ih	U73	K78	60	120	42	30{4}+12{10/3}
110	Small snub icosicosidodecahedron Small snub icosicosidodecahedron In geometry, the small snub icosicosidodecahedron is a uniform star polyhedron, indexed as U32. It has 112 faces , 180 edges, and 60 vertices.- Convex hull :Its convex hull is a nonuniform truncated icosahedron....		Small hexagonal hexecontahedron Small hexagonal hexecontahedron In geometry, the small hexagonal hexecontahedron is a nonconvex isohedral polyhedron. It is the dual of the uniform small snub icosicosidodecahedron. It is partially degenerate, having coincident vertices, as its dual has coplanar triangular faces....		|5/23 3	3.3.3.3.3.5/2	Ih	U32	K37	60	180	112	(40+60){3}+12{5/2}
111	Snub dodecadodecahedron		Medial pentagonal hexecontahedron Medial pentagonal hexecontahedron In geometry, the medial pentagonal hexecontahedron is a nonconvex isohedral polyhedron. It is the dual of the snub dodecadodecahedron. It has 60 intersecting irregular pentagonal faces.- External links :*...		|25/25	3.3.5/2.3.5	I	U40	K45	60	150	84	60{3}+12{5}+12{5/2}
112	Snub icosidodecadodecahedron Snub icosidodecadodecahedron In geometry, the snub icosidodecadodecahedron is a nonconvex uniform polyhedron, indexed as U46.- Cartesian coordinates :Cartesian coordinates for the vertices of a snub icosidodecadodecahedron are all the even permutations of...		Medial hexagonal hexecontahedron Medial hexagonal hexecontahedron In geometry, the small ditrigonal dodecacronic hexecontahedron is a nonconvex isohedral polyhedron. It is the dual of the uniform snub icosidodecadodecahedron....		|5/33 5	3.3.3.3.5.5/3	I	U46	K51	60	180	104	(20+6){3}+12{5}+12{5/2}
113	Great inverted snub icosidodecahedron		Great inverted pentagonal hexecontahedron Great inverted pentagonal hexecontahedron In geometry, the great inverted pentagonal hexecontahedron is a nonconvex isohedral polyhedron. It's composed of 60 self-intersecting pentagonal faces, 150 edges and 92 vertices.It is the dual of the uniform great inverted snub icosidodecahedron....		|5/32 3	3.3.3.3.5/3	I	U69	K74	60	150	92	(20+60){3}+12{5/2}
114	Inverted snub dodecadodecahedron		Medial inverted pentagonal hexecontahedron Medial inverted pentagonal hexecontahedron In geometry, the medial inverted pentagonal hexecontahedron is a nonconvex isohedral polyhedron. It is the dual of the uniform inverted snub dodecadodecahedron....		|5/32 5	3.5/3.3.3.5	I	U60	K65	60	150	84	60{3}+12{5}+12{5/2}
115	Great snub dodecicosidodecahedron Great snub dodecicosidodecahedron In geometry, the great snub dodecicosidodecahedron is a nonconvex uniform polyhedron, indexed as U64.- Related polyhedra :It shares its vertices and edges, as well as 20 of its triangular faces and all its pentagrammic faces, with the great dirhombicosidodecahedron,...		Great hexagonal hexecontahedron Great hexagonal hexecontahedron In geometry, the great hexagonal hexecontahedron is a nonconvex isohedral polyhedron. It is the dual of the uniform great snub dodecicosidodecahedron....		|5/35/23	3.5/3.3.5/2.3.3	I	U64	K69	60	180	104	(20+60){3}+(12+12){5/2}
116	Great snub icosidodecahedron		Great pentagonal hexecontahedron Great pentagonal hexecontahedron In geometry, the great pentagonal hexecontahedron is a nonconvex isohedral polyhedron. It is the dual of the great snub icosidodecahedron. It has 60 intersecting irregular pentagonal faces, 120 edges, and 92 vertices.- External links :*...		|25/25/2	3.3.3.3.5/2	I	U57	K62	60	150	92	(20+60){3}+12{5/2}
117	Great retrosnub icosidodecahedron		Great pentagrammic hexecontahedron Great pentagrammic hexecontahedron In geometry, the great pentagrammic hexecontahedron is a nonconvex isohedral polyhedron. It is the dual of the great retrosnub icosidodecahedron....		|3/25/32	(3.3.3.3.5/3)/2	I	U74	K79	60	150	92	(20+60){3}+12{5/2}
118	Small retrosnub icosicosidodecahedron Small retrosnub icosicosidodecahedron In geometry, the small retrosnub icosicosidodecahedron is a nonconvex uniform polyhedron, indexed as U72.- Convex hull :Its convex hull is a nonuniform truncated dodecahedron.- Cartesian coordinates :...		Small hexagrammic hexecontahedron Small hexagrammic hexecontahedron In geometry, the small hexagrammic hexecontahedron is a nonconvex isohedral polyhedron. It is the dual of the small retrosnub icosicosidodecahedron. It is partially degenerate, having coincident vertices, as its dual has coplanar triangular faces....		|3/23/25/2	(3.3.3.3.3.5/2)/2	Ih	U72	K77	180	60	112	(40+60){3}+12{5/2}
119	Great dirhombicosidodecahedron Great dirhombicosidodecahedron In geometry, the great dirhombicosidodecahedron is a nonconvex uniform polyhedron, indexed last as U75.This is the only uniform polyhedron with more than six faces meeting at a vertex...		Great dirhombicosidodecacron Great dirhombicosidodecacron In geometry, the great dirhombicosidodecacron is a nonconvex isohedral polyhedron. It is the dual of the great dirhombicosidodecahedron.In Magnus Wenninger's Dual Models, it is represented with intersecting infinite prisms passing through the model center, cut off at a certain point that is...		|3/25/335/2	(4.5/3.4.3.4.5/2.4.3/2)/2	Ih	U75	K80	60	240	124	40{3}+60{4}+24{5/2}

External links

• Magnus J. Wenninger
• Software used to generate images in this article:
  • Stella: Polyhedron Navigator Stella (software)
    Stella (software)
    Stella, a computer program available in three versions was created by Robert Webb of Australia...
    
    - Can create and print nets for all of Wenninger's polyhedron models.
  • Vladimir Bulatov's Polyhedra Stellations Applet
• M. Wenninger, Polyhedron Models, Errata: known errors in the various editions.