Compound of five tetrahedra
Type	Regular compound
Index	UC5, W24
Elements Euler characteristic In mathematics, and more specifically in algebraic topology and polyhedral combinatorics, the Euler characteristic is a topological invariant, a number that describes a topological space's shape or structure regardless of the way it is bent... (As a compound)	5 tetrahedra Tetrahedron In geometry, a tetrahedron is a polyhedron composed of four triangular faces, three of which meet at each vertex. A regular tetrahedron is one in which the four triangles are regular, or "equilateral", and is one of the Platonic solids... : F = 20, E = 30, V = 20
Dual compound Dual polyhedron In geometry, polyhedra are associated into pairs called duals, where the vertices of one correspond to the faces of the other. The dual of the dual is the original polyhedron. The dual of a polyhedron with equivalent vertices is one with equivalent faces, and of one with equivalent edges is another...	Self-dual
Symmetry group Symmetry group The symmetry group of an object is the group of all isometries under which it is invariant with composition as the operation...	chiral Chirality (mathematics) In geometry, a figure is chiral if it is not identical to its mirror image, or, more precisely, if it cannot be mapped to its mirror image by rotations and translations alone. For example, a right shoe is different from a left shoe, and clockwise is different from counterclockwise.A chiral object...  icosahedral Icosahedral symmetry A regular icosahedron has 60 rotational symmetries, and a symmetry order of 120 including transformations that combine a reflection and a rotation...  (I)
Subgroup Subgroup In group theory, given a group G under a binary operation *, a subset H of G is called a subgroup of G if H also forms a group under the operation *. More precisely, H is a subgroup of G if the restriction of * to H x H is a group operation on H...  restricting to one constituent	chiral Chirality (mathematics) In geometry, a figure is chiral if it is not identical to its mirror image, or, more precisely, if it cannot be mapped to its mirror image by rotations and translations alone. For example, a right shoe is different from a left shoe, and clockwise is different from counterclockwise.A chiral object...  tetrahedral Tetrahedral symmetry 150px|right|thumb|A regular [[tetrahedron]], an example of a solid with full tetrahedral symmetryA regular tetrahedron has 12 rotational symmetries, and a symmetry order of 24 including transformations that combine a reflection and a rotation.The group of all symmetries is isomorphic to the group...  (T)
Stellation diagram Stellation diagram In geometry, a stellation diagram or stellation pattern is a two-dimensional diagram in the plane of some face of a polyhedron, showing lines where other face planes intersect with this one. The lines cause 2D space to be divided up into regions. Regions not intersected by any further lines are... Stellation Stellation Stellation is a process of constructing new polygons , new polyhedra in three dimensions, or, in general, new polytopes in n dimensions. The process consists of extending elements such as edges or face planes, usually in a symmetrical way, until they meet each other again...  core Convex hull Convex hull In mathematics, the convex hull or convex envelope for a set of points X in a real vector space V is the minimal convex set containing X.... Icosahedron Dodecahedron

This compound polyhedron

Polyhedron

In elementary geometry a polyhedron is a geometric solid in three dimensions with flat faces and straight edges...

 is also a stellation

Stellation

Stellation is a process of constructing new polygons , new polyhedra in three dimensions, or, in general, new polytopes in n dimensions. The process consists of extending elements such as edges or face planes, usually in a symmetrical way, until they meet each other again...

 of the regular icosahedron

Icosahedron

In geometry, an icosahedron is a regular polyhedron with 20 identical equilateral triangular faces, 30 edges and 12 vertices. It is one of the five Platonic solids....

. It was first described by Edmund Hess

Edmund Hess

Edmund Hess was a German mathematician who discovered several regular polytopes.- References :* Regular Polytopes, , Dover edition, ISBN 0-486-61480-8...

 in 1876.

As a compound

It can be constructed by arranging five tetrahedra

Tetrahedron

In geometry, a tetrahedron is a polyhedron composed of four triangular faces, three of which meet at each vertex. A regular tetrahedron is one in which the four triangles are regular, or "equilateral", and is one of the Platonic solids...

 in rotational icosahedral symmetry (I), as colored in the upper right model. It is one of five regular compounds which can be constructed from identical Platonic solid

Platonic solid

In geometry, a Platonic solid is a convex polyhedron that is regular, in the sense of a regular polygon. Specifically, the faces of a Platonic solid are congruent regular polygons, with the same number of faces meeting at each vertex; thus, all its edges are congruent, as are its vertices and...

s.

It shares the same vertex arrangement

Vertex arrangement

In geometry, a vertex arrangement is a set of points in space described by their relative positions. They can be described by their use in polytopes....

 as a regular dodecahedron.

There are two enantiomorphous

Chirality (mathematics)

In geometry, a figure is chiral if it is not identical to its mirror image, or, more precisely, if it cannot be mapped to its mirror image by rotations and translations alone. For example, a right shoe is different from a left shoe, and clockwise is different from counterclockwise.A chiral object...

 forms (the same figure but having opposite chirality) of this compound polyhedron. Both forms together create the reflection symmetric compound of ten tetrahedra

Compound of ten tetrahedra

This polyhedron can be seen as either a polyhedral stellation or a compound. This compound was first described by Edmund Hess in 1876.- As a compound :It can also be seen as the compound of ten tetrahedra with full icosahedral symmetry...

.

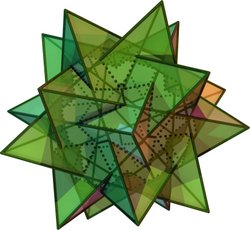
Transparent Models (Animation)

As a stellation

It can also be obtained by stellating

Stellation

Stellation is a process of constructing new polygons , new polyhedra in three dimensions, or, in general, new polytopes in n dimensions. The process consists of extending elements such as edges or face planes, usually in a symmetrical way, until they meet each other again...

 the icosahedron

Icosahedron

In geometry, an icosahedron is a regular polyhedron with 20 identical equilateral triangular faces, 30 edges and 12 vertices. It is one of the five Platonic solids....

, and is given as Wenninger model index 24.

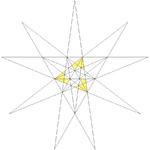
As a facetting

It is a facetting

Facetting

In geometry, facetting is the process of removing parts of a polygon, polyhedron or polytope, without creating any new vertices.Facetting is the reciprocal or dual process to stellation...

 of a dodecahedron, as shown at left.

Group theory

The compound of five tetrahedra is a geometric illustration of the notion of orbits and stabilizers, as follows.

The symmetry group of the compound is the (rotational) icosahedral group I of order 60, while the stabilizer of a single chosen tetrahedron is the (rotational) tetrahedral group T of order 12, and the orbit space I/T (of order 60/12 = 5) is naturally identified with the 5 tetrahedra – the coset gT corresponds to which tetrahedron g sends the chosen tetrahedron to.

An unusual dual property

This compound is unusual, in that the dual

Dual polyhedron

In geometry, polyhedra are associated into pairs called duals, where the vertices of one correspond to the faces of the other. The dual of the dual is the original polyhedron. The dual of a polyhedron with equivalent vertices is one with equivalent faces, and of one with equivalent edges is another...

 figure is the enantiomorph of the original. This property seems to have led to a widespread idea that the dual of any chiral

Chirality (mathematics)

In geometry, a figure is chiral if it is not identical to its mirror image, or, more precisely, if it cannot be mapped to its mirror image by rotations and translations alone. For example, a right shoe is different from a left shoe, and clockwise is different from counterclockwise.A chiral object...

 figure has the opposite chirality. The idea is generally quite false: a chiral dual nearly always has the same chirality as its twin. For example if a polyhedron has a right hand twist, then its dual

Dual polyhedron

In geometry, polyhedra are associated into pairs called duals, where the vertices of one correspond to the faces of the other. The dual of the dual is the original polyhedron. The dual of a polyhedron with equivalent vertices is one with equivalent faces, and of one with equivalent edges is another...

 will also have a right hand twist.

In the case of the compound of five tetrahedra, if the faces are twisted to the right then the vertices are twisted to the left. When we dualise

Dual polyhedron

In geometry, polyhedra are associated into pairs called duals, where the vertices of one correspond to the faces of the other. The dual of the dual is the original polyhedron. The dual of a polyhedron with equivalent vertices is one with equivalent faces, and of one with equivalent edges is another...

, the faces dualise to right-twisted vertices and the vertices dualise to left-twisted faces, giving the chiral twin. Figures with this property are extremely rare.

External links

• Metal Sculpture of Five Tetrahedra Compound
• VRML
  VRML
  VRML is a standard file format for representing 3-dimensional interactive vector graphics, designed particularly with the World Wide Web in mind...
  
   model: http://interocitors.com/polyhedra/UCs/05__5_Tetrahedra.wrl
• Compounds of 5 and 10 Tetrahedra by Sándor Kabai, The Wolfram Demonstrations Project.