Great triambic icosahedron	Medial triambic icosahedron
Types	Dual uniform polyhedra Nonconvex uniform polyhedron In geometry, a uniform star polyhedron is a self-intersecting uniform polyhedron. They are also sometimes called nonconvex polyhedra to imply self-intersecting...
Symmetry group	Ih
Name	Great triambic icosahedron	Medial triambic icosahedron
Index references	DU Uniform polyhedron A uniform polyhedron is a polyhedron which has regular polygons as faces and is vertex-transitive... 47, W34, 30/59	DU Uniform polyhedron A uniform polyhedron is a polyhedron which has regular polygons as faces and is vertex-transitive... 41, W34, 30/59
Elements Euler characteristic In mathematics, and more specifically in algebraic topology and polyhedral combinatorics, the Euler characteristic is a topological invariant, a number that describes a topological space's shape or structure regardless of the way it is bent...	F = 20, E = 60 V = 32 (χ = -8)	F = 20, E = 60 V = 24 (χ = -16)
Isohedral faces
Duals Dual polyhedron In geometry, polyhedra are associated into pairs called duals, where the vertices of one correspond to the faces of the other. The dual of the dual is the original polyhedron. The dual of a polyhedron with equivalent vertices is one with equivalent faces, and of one with equivalent edges is another...	Great ditrigonal icosidodecahedron	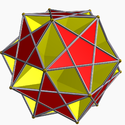Ditrigonal dodecadodecahedron Ditrigonal dodecadodecahedron In geometry, the Ditrigonal dodecadodecahedron is a nonconvex uniform polyhedron, indexed as U41.- Related polyhedra :Its convex hull is a regular dodecahedron...
Stellation Stellation Stellation is a process of constructing new polygons , new polyhedra in three dimensions, or, in general, new polytopes in n dimensions. The process consists of extending elements such as edges or face planes, usually in a symmetrical way, until they meet each other again...
Icosahedron Icosahedron In geometry, an icosahedron is a regular polyhedron with 20 identical equilateral triangular faces, 30 edges and 12 vertices. It is one of the five Platonic solids.... : W34
Stellation diagram Stellation diagram In geometry, a stellation diagram or stellation pattern is a two-dimensional diagram in the plane of some face of a polyhedron, showing lines where other face planes intersect with this one. The lines cause 2D space to be divided up into regions. Regions not intersected by any further lines are...

In geometry

Geometry

Geometry arose as the field of knowledge dealing with spatial relationships. Geometry was one of the two fields of pre-modern mathematics, the other being the study of numbers ....

, the great triambic icosahedron and medial triambic icosahedron are visually identical dual

Dual polyhedron

In geometry, polyhedra are associated into pairs called duals, where the vertices of one correspond to the faces of the other. The dual of the dual is the original polyhedron. The dual of a polyhedron with equivalent vertices is one with equivalent faces, and of one with equivalent edges is another...

 uniform polyhedra. The exterior surface also represents the De₁f₁ stellation of the icosahedron

Icosahedron

In geometry, an icosahedron is a regular polyhedron with 20 identical equilateral triangular faces, 30 edges and 12 vertices. It is one of the five Platonic solids....

. The only way to differentiate these two polyhedra is to mark which intersections between edges are true vertices

Vertex

Vertex may refer to:-Mathematics:*Vertex , an angle point of any shape or angle*Vertex , a node in a graph*Vertex , a local extreme point of curvature...

 and which are not. In the above images, true vertices are marked by gold spheres.

The 12 vertices of the convex hull

Convex hull

In mathematics, the convex hull or convex envelope for a set of points X in a real vector space V is the minimal convex set containing X....

 matches the vertex arrangement

Vertex arrangement

In geometry, a vertex arrangement is a set of points in space described by their relative positions. They can be described by their use in polytopes....

 of an icosahedron

Icosahedron

In geometry, an icosahedron is a regular polyhedron with 20 identical equilateral triangular faces, 30 edges and 12 vertices. It is one of the five Platonic solids....

.

Great triambic icosahedron

The great triambic icosahedron is the dual of the great ditrigonal icosidodecahedron, U47. It has 20 inverted-hexagonal faces, shaped like a three-bladed propeller

Propeller

A propeller is a type of fan that transmits power by converting rotational motion into thrust. A pressure difference is produced between the forward and rear surfaces of the airfoil-shaped blade, and a fluid is accelerated behind the blade. Propeller dynamics can be modeled by both Bernoulli's...

. It has 32 vertices: 12 exterior points, and 20 hidden inside. It has 60 edges.

Medial triambic icosahedron

The medial triambic icosahedron is the dual of the ditrigonal dodecadodecahedron

Ditrigonal dodecadodecahedron

In geometry, the Ditrigonal dodecadodecahedron is a nonconvex uniform polyhedron, indexed as U41.- Related polyhedra :Its convex hull is a regular dodecahedron...

, U41. It has 20 faces, each being simple concave isogonal hexagons. It has 24 vertices: 12 exterior points, and 12 hidden inside. It has 60 edges.

Unlike the great triambic icosahedron, the medial triambic icosahedron is topologically a regular polyhedron

Regular polyhedron

A regular polyhedron is a polyhedron whose faces are congruent regular polygons which are assembled in the same way around each vertex. A regular polyhedron is highly symmetrical, being all of edge-transitive, vertex-transitive and face-transitive - i.e. it is transitive on its flags...

 of index two. By distorting the triambi into regular hexagons, one obtains the hyperbolic

Hyperbolic geometry

In mathematics, hyperbolic geometry is a non-Euclidean geometry, meaning that the parallel postulate of Euclidean geometry is replaced...

 order-5 hexagonal tiling:

As a stellation

It is Wenninger's

Magnus Wenninger

Father Magnus J. Wenninger OSB is a mathematician who works on constructing polyhedron models, and wrote the first book on their construction.-Early life and education:...

 34th model in his 9th stellation of the icosahedron

External links

• gratrix.net Uniform polyhedra and duals
• bulatov.org Medial triambic icosahedron Great triambic icosahedron