Spacetime algebra
Encyclopedia
In mathematical physics
, spacetime algebra (STA) is a name for the Clifford algebra
Cℓ1,3(R),or Geometric algebra
G4 = G(M4
) which can be particularly closely associated with the geometry of special relativity
and relativistic spacetime
.
It is a linear algebra
allowing not just vectors, but also directed quantities associated with particular planes
(for example: areas, or rotations) or associated with particular (hyper-)volume
s to be combined, as well as rotated
, reflected
, or Lorentz boosted. It is also the natural parent algebra of spinor
s in special relativity. These properties allow many of the most important equations in physics to be expressed in particularly simple forms; and can be very helpful towards a more geometrical understanding of their meanings.
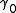and three orthogonal space-like vectors, 
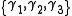, under the multiplication rule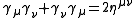
where
is the Minkowski metric with signature (+ − − −)
Thus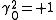
, 
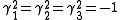, otherwise 
.
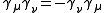The basis vectors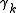
share the same properties as the Dirac matrices, but no explicit matrix representation is utilized in STA.
This generates a basis of one scalar
,
, four vectors 
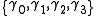, six bivector
s
, four pseudovector
s
and one pseudoscalar
.
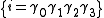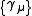is the reciprocal basis 
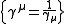, satisfying the relation
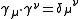
These reciprocal frame vectors differ only by a sign, with
, and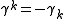 
.
A vector may be represented in either upper or lower index coordinates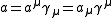
, where the coordinates may be extracted by taking dot products with the basis vectors or their reciprocals
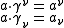
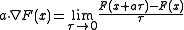
One can show that this requires the definition of the gradient to be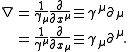
Written out explicitly with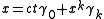
, these partials are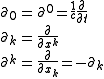
serves to split a four vector into a scalar timelike and a bivector spacelike component. With 
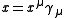we have
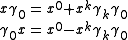
As these bivectors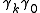
square to unity, they serve as a spatial basis. Utilizing the Pauli matrix notation, these are written 
. Spatial vectors in STA are denoted in boldface; for the spacetime split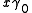 
one therefore writes
where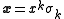
.
, because it contains idempotents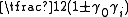
and zero divisor
s: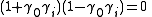
. These can be interpreted as projectors onto the light-cone and orthogonality relations for such projectors, respectively. But in general it is possible to divide one multivector quantity by another, and make sense of the result: so, for example, a directed area divided by a vector in the same plane gives another vector, orthogonal to the first.
, i.e.
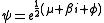
where ϕ is a bivector, so that
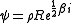
where R is viewed as a Lorentz rotation; David Hestenes
interprets this equation as connecting spin with the imaginary pseudoscalar, and others have extended this to provide a framework for locally varying vector- and scalar-valued observables and support for the Zitterbewegung
interpretation of quantum mechanics originally proposed by Schrödinger.
while admitting a gauge symmetry under "arbitrary smooth remapping of events onto spacetime" (Lasenby, et al.); a nontrivial proof then leads to the geodesic equation,
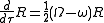
and the covariant derivative
,
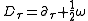where ω is the connexion associated with the gravitational potential, and Ω is an external interaction such as an electromagnetic field.
The theory shows some promise for the treatment of black holes, as its form of the Schwarzschild solution does not break down at singularities; most of the results of General Relativity
have been mathematically reproduced, and the relativistic formulation of classical electrodynamics has been extended to quantum mechanics
and the dirac equation
.
Mathematical physics
Mathematical physics refers to development of mathematical methods for application to problems in physics. The Journal of Mathematical Physics defines this area as: "the application of mathematics to problems in physics and the development of mathematical methods suitable for such applications and...
, spacetime algebra (STA) is a name for the Clifford algebra
Clifford algebra
In mathematics, Clifford algebras are a type of associative algebra. As K-algebras, they generalize the real numbers, complex numbers, quaternions and several other hypercomplex number systems. The theory of Clifford algebras is intimately connected with the theory of quadratic forms and orthogonal...
Cℓ1,3(R),or Geometric algebra
Geometric algebra
Geometric algebra , together with the associated Geometric calculus, provides a comprehensive alternative approach to the algebraic representation of classical, computational and relativistic geometry. GA now finds application in all of physics, in graphics and in robotics...
G4 = G(M4
Minkowski space
In physics and mathematics, Minkowski space or Minkowski spacetime is the mathematical setting in which Einstein's theory of special relativity is most conveniently formulated...
) which can be particularly closely associated with the geometry of special relativity
Special relativity
Special relativity is the physical theory of measurement in an inertial frame of reference proposed in 1905 by Albert Einstein in the paper "On the Electrodynamics of Moving Bodies".It generalizes Galileo's...
and relativistic spacetime
Spacetime
In physics, spacetime is any mathematical model that combines space and time into a single continuum. Spacetime is usually interpreted with space as being three-dimensional and time playing the role of a fourth dimension that is of a different sort from the spatial dimensions...
.
It is a linear algebra
Linear algebra
Linear algebra is a branch of mathematics that studies vector spaces, also called linear spaces, along with linear functions that input one vector and output another. Such functions are called linear maps and can be represented by matrices if a basis is given. Thus matrix theory is often...
allowing not just vectors, but also directed quantities associated with particular planes
Bivector
In mathematics, a bivector or 2-vector is a quantity in geometric algebra or exterior algebra that generalises the idea of a vector. If a scalar is considered a zero dimensional quantity, and a vector is a one dimensional quantity, then a bivector can be thought of as two dimensional. Bivectors...
(for example: areas, or rotations) or associated with particular (hyper-)volume
Multivector
In multilinear algebra, a multivector or clif is an element of the exterior algebra on a vector space, \Lambda^* V. This algebra consists of linear combinations of simple k-vectors v_1\wedge\cdots\wedge v_k."Multivector" may mean either homogeneous elements In multilinear algebra, a multivector...
s to be combined, as well as rotated
Rotation
A rotation is a circular movement of an object around a center of rotation. A three-dimensional object rotates always around an imaginary line called a rotation axis. If the axis is within the body, and passes through its center of mass the body is said to rotate upon itself, or spin. A rotation...
, reflected
Reflection (mathematics)
In mathematics, a reflection is a mapping from a Euclidean space to itself that is an isometry with a hyperplane as set of fixed points; this set is called the axis or plane of reflection. The image of a figure by a reflection is its mirror image in the axis or plane of reflection...
, or Lorentz boosted. It is also the natural parent algebra of spinor
Spinor
In mathematics and physics, in particular in the theory of the orthogonal groups , spinors are elements of a complex vector space introduced to expand the notion of spatial vector. Unlike tensors, the space of spinors cannot be built up in a unique and natural way from spatial vectors...
s in special relativity. These properties allow many of the most important equations in physics to be expressed in particularly simple forms; and can be very helpful towards a more geometrical understanding of their meanings.
Structure
The spacetime algebra is built up from combinations of one time-like basis vector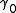 and three orthogonal space-like vectors, 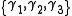, under the multiplication rule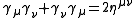where
is the Minkowski metric with signature (+ − − −)Thus
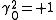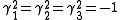, , otherwise 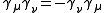.The basis vectors
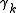share the same properties as the Dirac matrices, but no explicit matrix representation is utilized in STA.This generates a basis of one scalar
Scalar (mathematics)
In linear algebra, real numbers are called scalars and relate to vectors in a vector space through the operation of scalar multiplication, in which a vector can be multiplied by a number to produce another vector....
,
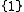, four vectors 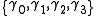, six bivectorBivector
In mathematics, a bivector or 2-vector is a quantity in geometric algebra or exterior algebra that generalises the idea of a vector. If a scalar is considered a zero dimensional quantity, and a vector is a one dimensional quantity, then a bivector can be thought of as two dimensional. Bivectors...
s
, four pseudovectorPseudovector
In physics and mathematics, a pseudovector is a quantity that transforms like a vector under a proper rotation, but gains an additional sign flip under an improper rotation such as a reflection. Geometrically it is the opposite, of equal magnitude but in the opposite direction, of its mirror image...
s
and one pseudoscalarPseudoscalar
In physics, a pseudoscalar is a quantity that behaves like a scalar, except that it changes sign under a parity inversion such as improper rotations while a true scalar does not.The prototypical example of a pseudoscalar is the scalar triple product...
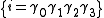.Reciprocal frame.
Associated with the basis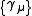 is the reciprocal basis 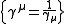, satisfying the relation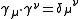These reciprocal frame vectors differ only by a sign, with
, and 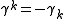.A vector may be represented in either upper or lower index coordinates
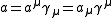, where the coordinates may be extracted by taking dot products with the basis vectors or their reciprocals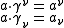Space time gradient
The spacetime gradient, like the gradient in a Euclidean space, is defined such that the directional derivative relationship is satisfied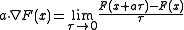One can show that this requires the definition of the gradient to be
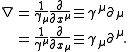
Written out explicitly with
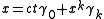, these partials are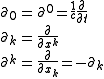Space time split
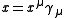Pre or post multiplication by the time like basis vector serves to split a four vector into a scalar timelike and a bivector spacelike component. With we have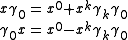As these bivectors
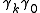square to unity, they serve as a spatial basis. Utilizing the Pauli matrix notation, these are written . Spatial vectors in STA are denoted in boldface; for the spacetime split 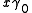one therefore writeswhere
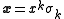.Multivector division
The spacetime algebra is not a formal division algebraDivision algebra
In the field of mathematics called abstract algebra, a division algebra is, roughly speaking, an algebra over a field, in which division is possible.- Definitions :...
, because it contains idempotents
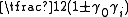and zero divisorZero divisor
In abstract algebra, a nonzero element a of a ring is a left zero divisor if there exists a nonzero b such that ab = 0. Similarly, a nonzero element a of a ring is a right zero divisor if there exists a nonzero c such that ca = 0. An element that is both a left and a right zero divisor is simply...
s:
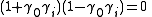. These can be interpreted as projectors onto the light-cone and orthogonality relations for such projectors, respectively. But in general it is possible to divide one multivector quantity by another, and make sense of the result: so, for example, a directed area divided by a vector in the same plane gives another vector, orthogonal to the first.In relativistic quantum mechanics
The relativistic quantum wavefunction is sometimes expressed as a spinor fieldSpinor field
In particle physics, a spinor field of order 2s describes a particle of spin s, where s is an integer or half-integer. Therefore, a spinor of order 2s contains as much information as a tensor of order s...
, i.e.
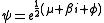
where ϕ is a bivector, so that
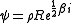
where R is viewed as a Lorentz rotation; David Hestenes
David Hestenes
David Orlin Hestenes, Ph.D. is a physicist. For more than 30 years, he was employed in the Department of Physics and Astronomy of Arizona State University , where he retired with the rank of Research Professor and is now emeritus....
interprets this equation as connecting spin with the imaginary pseudoscalar, and others have extended this to provide a framework for locally varying vector- and scalar-valued observables and support for the Zitterbewegung
Zitterbewegung
Zitterbewegung is a theoretical rapid motion of elementary particles, in particular electrons, that obey the Dirac equation...
interpretation of quantum mechanics originally proposed by Schrödinger.
In a new formulation of General Relativity
Lasenby, Doran, and Gull of Cambridge University have proposed a new formulation of gravity, termed Gauge-Theory Gravity (GTG), wherein Spacetime Algebra is used to induce curvature on Minkowski spaceMinkowski space
In physics and mathematics, Minkowski space or Minkowski spacetime is the mathematical setting in which Einstein's theory of special relativity is most conveniently formulated...
while admitting a gauge symmetry under "arbitrary smooth remapping of events onto spacetime" (Lasenby, et al.); a nontrivial proof then leads to the geodesic equation,
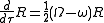
and the covariant derivative
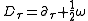,where ω is the connexion associated with the gravitational potential, and Ω is an external interaction such as an electromagnetic field.
The theory shows some promise for the treatment of black holes, as its form of the Schwarzschild solution does not break down at singularities; most of the results of General Relativity
General relativity
General relativity or the general theory of relativity is the geometric theory of gravitation published by Albert Einstein in 1916. It is the current description of gravitation in modern physics...
have been mathematically reproduced, and the relativistic formulation of classical electrodynamics has been extended to quantum mechanics
Quantum mechanics
Quantum mechanics, also known as quantum physics or quantum theory, is a branch of physics providing a mathematical description of much of the dual particle-like and wave-like behavior and interactions of energy and matter. It departs from classical mechanics primarily at the atomic and subatomic...
and the dirac equation
Dirac equation
The Dirac equation is a relativistic quantum mechanical wave equation formulated by British physicist Paul Dirac in 1928. It provided a description of elementary spin-½ particles, such as electrons, consistent with both the principles of quantum mechanics and the theory of special relativity, and...
.
See also
- Geometric algebraGeometric algebraGeometric algebra , together with the associated Geometric calculus, provides a comprehensive alternative approach to the algebraic representation of classical, computational and relativistic geometry. GA now finds application in all of physics, in graphics and in robotics...
- Dirac algebraDirac algebraIn mathematical physics, the Dirac algebra is the Clifford algebra Cℓ1,3 which is generated by matrix multiplication and real and complex linear combination over the Dirac gamma matrices, introduced by the mathematical physicist P. A. M...
- Dirac equationDirac equationThe Dirac equation is a relativistic quantum mechanical wave equation formulated by British physicist Paul Dirac in 1928. It provided a description of elementary spin-½ particles, such as electrons, consistent with both the principles of quantum mechanics and the theory of special relativity, and...
- General RelativityGeneral relativityGeneral relativity or the general theory of relativity is the geometric theory of gravitation published by Albert Einstein in 1916. It is the current description of gravitation in modern physics...