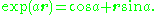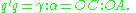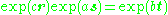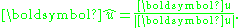Versor
Encyclopedia
In modern algebra, a versor is a quaternion
of norm
one. Every versor is of the form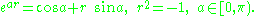
Such a versor may be viewed as a directed great-circle
arc
with axis r and length a. In case a = π/2, the versor is a right versor. In linear algebra
, geometry
, and physics
, the term versor is often used for a right versor. In this case, a versor is defined as a unit vector indicating the orientation
of a directed axis in a Cartesian coordinate system
.
The word is from Latin versus = "turned", from pp. of vertere = "to turn", and was introduced by William Rowan Hamilton
, in the context of his quaternion theory.
Hamilton denoted the versor of a quaternion q by the symbol Uq. He was then able to display the general quaternion in polar coordinate form
where Tq is the norm of q. The tensor of a versor is always equal to one.
Of particular importance are the right versors, which have angle π/2. These versors have zero scalar part, and so are vectors of length one (unit vectors). The right versors form a sphere of square roots of −1 in the quaternion algebra. The generators i, j, and k in the quaternion group
are examples of right versors.
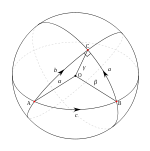
If a great-circle arc has length a, and if
is the pole of this great circle (viewed as the equator with respect to the pole), then the versor is the quaternion
Multiplication of quaternions of norm one corresponds to the "addition" of great circle arcs on the 2-sphere. Hamilton writes
imply
The algebra of versors has been exploited to exhibit the properties of elliptic space.
Since versors correspond to elements of the 3-sphere
in H, it is natural today to write
for the versor composition, where
is the pole of the product versor and b is its angle (as in the figure).
When we view the spherical trigonometric solution for b and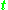
in the product of exponentials, then we have an instance of the general Campbell-Baker-Hausdorff formula in Lie group
theory. As the 3-sphere represented by versors in H is a 3-parameter Lie group, practice with versor compositions is good preparation for more abstract Lie group and Lie algebra theory. Indeed, as great circle arcs they compose as sums of vector arcs (Hamilton's term), but as quaternions they simply multiply. Thus the great-circle-arc model is similar to logarithm in that sums correspond to products. In Lie theory
, the pair (group,algebra) carries this logarithm-likeness to higher dimensions.
, a hyperbolic versor is a quantity of the form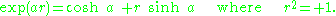
Such elements arise in algebras of mixed signature
, for example split-complex number
s or split-quaternions. It was the algebra of tessarines discovered by James Cockle in 1848 that first provided hyperbolic versors. In fact, James Cockle wrote the above equation (with r = j) when he found that the tessarines included the new type of imaginary element.
The primary exponent of hyperbolic versors was Alexander Macfarlane
as he worked to shape quaternion theory to serve physical science. He saw the modelling power of hyperbolic versors operating on the split-complex number plane, and in 1891 he introduced hyperbolic quaternion
s to extend the concept to 4-space. Problems in that algebra led to use of biquaternions after 1900. In a widely circulated review of 1899, Macfarlane said:
Today the concept of a one-parameter group
subsumes the concepts of versor and hyperbolic versor as the terminology of Sophus Lie
has replaced that of Hamilton and Macfarlane.
In particular, for each r such that r r = +1 or r r = −1, the mapping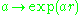
takes the real line to a group of hyperbolic or ordinary versors. In the ordinary case, when r and −r are antipodal point
s on a sphere, the one-parameter groups have the same points but are oppositely directed. In physics, this aspect of rotational symmetry
is termed a doublet (physics)
.
In 1911 Alfred Robb
published his Optical Geometry of Motion in which he identified the parameter rapidity
which specifies a change in frame of reference
. This rapidity parameter corresponds to the real variable in a one-parameter group of hyperbolic versors. With the further development of special relativity
the action of a hyperbolic versor came to be called a Lorentz boost.
Quaternion
In mathematics, the quaternions are a number system that extends the complex numbers. They were first described by Irish mathematician Sir William Rowan Hamilton in 1843 and applied to mechanics in three-dimensional space...
of norm
Norm (mathematics)
In linear algebra, functional analysis and related areas of mathematics, a norm is a function that assigns a strictly positive length or size to all vectors in a vector space, other than the zero vector...
one. Every versor is of the form
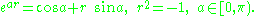
Such a versor may be viewed as a directed great-circle
Great circle
A great circle, also known as a Riemannian circle, of a sphere is the intersection of the sphere and a plane which passes through the center point of the sphere, as opposed to a general circle of a sphere where the plane is not required to pass through the center...
arc
Arc (geometry)
In geometry, an arc is a closed segment of a differentiable curve in the two-dimensional plane; for example, a circular arc is a segment of the circumference of a circle...
with axis r and length a. In case a = π/2, the versor is a right versor. In linear algebra
Linear algebra
Linear algebra is a branch of mathematics that studies vector spaces, also called linear spaces, along with linear functions that input one vector and output another. Such functions are called linear maps and can be represented by matrices if a basis is given. Thus matrix theory is often...
, geometry
Geometry
Geometry arose as the field of knowledge dealing with spatial relationships. Geometry was one of the two fields of pre-modern mathematics, the other being the study of numbers ....
, and physics
Physics
Physics is a natural science that involves the study of matter and its motion through spacetime, along with related concepts such as energy and force. More broadly, it is the general analysis of nature, conducted in order to understand how the universe behaves.Physics is one of the oldest academic...
, the term versor is often used for a right versor. In this case, a versor is defined as a unit vector indicating the orientation
Orientation (geometry)
In geometry the orientation, angular position, or attitude of an object such as a line, plane or rigid body is part of the description of how it is placed in the space it is in....
of a directed axis in a Cartesian coordinate system
Cartesian coordinate system
A Cartesian coordinate system specifies each point uniquely in a plane by a pair of numerical coordinates, which are the signed distances from the point to two fixed perpendicular directed lines, measured in the same unit of length...
.
The word is from Latin versus = "turned", from pp. of vertere = "to turn", and was introduced by William Rowan Hamilton
William Rowan Hamilton
Sir William Rowan Hamilton was an Irish physicist, astronomer, and mathematician, who made important contributions to classical mechanics, optics, and algebra. His studies of mechanical and optical systems led him to discover new mathematical concepts and techniques...
, in the context of his quaternion theory.
Presentation on the sphere
where Tq is the norm of q. The tensor of a versor is always equal to one.
Of particular importance are the right versors, which have angle π/2. These versors have zero scalar part, and so are vectors of length one (unit vectors). The right versors form a sphere of square roots of −1 in the quaternion algebra. The generators i, j, and k in the quaternion group
Quaternion group
In group theory, the quaternion group is a non-abelian group of order eight, isomorphic to a certain eight-element subset of the quaternions under multiplication...
are examples of right versors.
If a great-circle arc has length a, and if
is the pole of this great circle (viewed as the equator with respect to the pole), then the versor is the quaternion
Multiplication of quaternions of norm one corresponds to the "addition" of great circle arcs on the 2-sphere. Hamilton writes
-
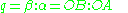and -
imply
The algebra of versors has been exploited to exhibit the properties of elliptic space.
Since versors correspond to elements of the 3-sphere
3-sphere
In mathematics, a 3-sphere is a higher-dimensional analogue of a sphere. It consists of the set of points equidistant from a fixed central point in 4-dimensional Euclidean space...
in H, it is natural today to write
for the versor composition, where
is the pole of the product versor and b is its angle (as in the figure).When we view the spherical trigonometric solution for b and
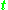in the product of exponentials, then we have an instance of the general Campbell-Baker-Hausdorff formula in Lie groupLie group
In mathematics, a Lie group is a group which is also a differentiable manifold, with the property that the group operations are compatible with the smooth structure...
theory. As the 3-sphere represented by versors in H is a 3-parameter Lie group, practice with versor compositions is good preparation for more abstract Lie group and Lie algebra theory. Indeed, as great circle arcs they compose as sums of vector arcs (Hamilton's term), but as quaternions they simply multiply. Thus the great-circle-arc model is similar to logarithm in that sums correspond to products. In Lie theory
Lie theory
Lie theory is an area of mathematics, developed initially by Sophus Lie.Early expressions of Lie theory are found in books composed by Lie with Friedrich Engel and Georg Scheffers from 1888 to 1896....
, the pair (group,algebra) carries this logarithm-likeness to higher dimensions.
Definition in linear algebra, geometry, and physics
Outside the context of quaternion theory, a versor is sometimes defined as a unit vector indicating the direction of a directed axis, or the direction of another vector. For instance:- The versors of a Cartesian coordinate systemCartesian coordinate systemA Cartesian coordinate system specifies each point uniquely in a plane by a pair of numerical coordinates, which are the signed distances from the point to two fixed perpendicular directed lines, measured in the same unit of length...
are the unit vectors codirectional with the axes of that system.
- The versor (or normalized vector)
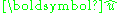of a non-zero vector 
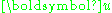is the unit vector codirectional with 
, i.e.,
-
- where
is the normNorm (mathematics)In linear algebra, functional analysis and related areas of mathematics, a norm is a function that assigns a strictly positive length or size to all vectors in a vector space, other than the zero vector...
(or length) of
.
- where
Hyperbolic versor
In linear algebraLinear algebra
Linear algebra is a branch of mathematics that studies vector spaces, also called linear spaces, along with linear functions that input one vector and output another. Such functions are called linear maps and can be represented by matrices if a basis is given. Thus matrix theory is often...
, a hyperbolic versor is a quantity of the form
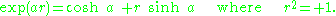
Such elements arise in algebras of mixed signature
Metric signature
The signature of a metric tensor is the number of positive and negative eigenvalues of the metric. That is, the corresponding real symmetric matrix is diagonalised, and the diagonal entries of each sign counted...
, for example split-complex number
Split-complex number
In abstract algebra, the split-complex numbers are a two-dimensional commutative algebra over the real numbers different from the complex numbers. Every split-complex number has the formwhere x and y are real numbers...
s or split-quaternions. It was the algebra of tessarines discovered by James Cockle in 1848 that first provided hyperbolic versors. In fact, James Cockle wrote the above equation (with r = j) when he found that the tessarines included the new type of imaginary element.
The primary exponent of hyperbolic versors was Alexander Macfarlane
Alexander Macfarlane
Alexander Macfarlane was a Nova Scotia lawyer and political figure. He was a member of the Canadian Senate from 1870 to 1898. His surname also appears as McFarlane in some sources....
as he worked to shape quaternion theory to serve physical science. He saw the modelling power of hyperbolic versors operating on the split-complex number plane, and in 1891 he introduced hyperbolic quaternion
Hyperbolic quaternion
In the abstract algebra of algebras over a field, the hyperbolic quaternionq = a + bi + cj + dk, \quad a,b,c,d \in R \!is a mutated quaternion wherei^2 = j^2 = k^2 = +1 \! instead of the usual −1....
s to extend the concept to 4-space. Problems in that algebra led to use of biquaternions after 1900. In a widely circulated review of 1899, Macfarlane said:
- …the root of a quadratic equation may be versor in nature or scalar in nature. If it is versor in nature, then the part affected by the radical involves the axis perpendicular to the plane of reference, and this is so, whether the radical involves the square root of minus one or not. In the former case the versor is circular, in the latter hyperbolic.
Today the concept of a one-parameter group
One-parameter group
In mathematics, a one-parameter group or one-parameter subgroup usually means a continuous group homomorphismfrom the real line R to some other topological group G...
subsumes the concepts of versor and hyperbolic versor as the terminology of Sophus Lie
Sophus Lie
Marius Sophus Lie was a Norwegian mathematician. He largely created the theory of continuous symmetry, and applied it to the study of geometry and differential equations.- Biography :...
has replaced that of Hamilton and Macfarlane.
In particular, for each r such that r r = +1 or r r = −1, the mapping
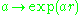takes the real line to a group of hyperbolic or ordinary versors. In the ordinary case, when r and −r are antipodal pointAntipodal point
In mathematics, the antipodal point of a point on the surface of a sphere is the point which is diametrically opposite to it — so situated that a line drawn from the one to the other passes through the centre of the sphere and forms a true diameter....
s on a sphere, the one-parameter groups have the same points but are oppositely directed. In physics, this aspect of rotational symmetry
Rotational symmetry
Generally speaking, an object with rotational symmetry is an object that looks the same after a certain amount of rotation. An object may have more than one rotational symmetry; for instance, if reflections or turning it over are not counted, the triskelion appearing on the Isle of Man's flag has...
is termed a doublet (physics)
Doublet (physics)
In quantum mechanics, a doublet is a quantum state of a system with a spin of 1/2, such that there are two allowed values of the spin component, −1/2 and +1/2. Quantum systems with two possible states are sometimes called two-level systems...
.
In 1911 Alfred Robb
Alfred Robb
Alfred Arthur Robb or Alfred A. Robb FRS was a British physicist.Robb studied at Queen's College in Belfast and at St John’s College in Cambridge. He then proceeded to University of Göttingen, where guided by Woldemar Voigt, he wrote his dissertation on the Zeeman effect. He also worked under J. J...
published his Optical Geometry of Motion in which he identified the parameter rapidity
Rapidity
In relativity, rapidity is an alternative to speed as a framework for measuring motion. On parallel velocities rapidities are simply additive, unlike speeds at relativistic velocities. For low speeds, rapidity and speed are proportional, but for high speeds, rapidity takes a larger value. The...
which specifies a change in frame of reference
Frame of reference
A frame of reference in physics, may refer to a coordinate system or set of axes within which to measure the position, orientation, and other properties of objects in it, or it may refer to an observational reference frame tied to the state of motion of an observer.It may also refer to both an...
. This rapidity parameter corresponds to the real variable in a one-parameter group of hyperbolic versors. With the further development of special relativity
Special relativity
Special relativity is the physical theory of measurement in an inertial frame of reference proposed in 1905 by Albert Einstein in the paper "On the Electrodynamics of Moving Bodies".It generalizes Galileo's...
the action of a hyperbolic versor came to be called a Lorentz boost.
External links
- http://www.biology-online.org/dictionary/versor
- http://www.thefreedictionary.com/Versor
- A. Macfarlane (1894) Papers on Space Analysis, B. Westerman, New York, weblink from archive.org.