
Blade (geometry)
Encyclopedia
In geometric algebra
, a blade is a generalization of the notion of vectors and scalars
to include bivector
s, trivectors, etc. In detail:
Geometric algebra
Geometric algebra , together with the associated Geometric calculus, provides a comprehensive alternative approach to the algebraic representation of classical, computational and relativistic geometry. GA now finds application in all of physics, in graphics and in robotics...
, a blade is a generalization of the notion of vectors and scalars
Scalar (mathematics)
In linear algebra, real numbers are called scalars and relate to vectors in a vector space through the operation of scalar multiplication, in which a vector can be multiplied by a number to produce another vector....
to include bivector
Bivector
In mathematics, a bivector or 2-vector is a quantity in geometric algebra or exterior algebra that generalises the idea of a vector. If a scalar is considered a zero dimensional quantity, and a vector is a one dimensional quantity, then a bivector can be thought of as two dimensional. Bivectors...
s, trivectors, etc. In detail:
- A scalar or 0-blade of grade 0 is the inner product or dot product of two vectors a and b denoted as:
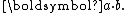
- A vector is a 1-blade of grade 1.
- A 2-blade of grade 2 is a simple bivectorBivectorIn mathematics, a bivector or 2-vector is a quantity in geometric algebra or exterior algebra that generalises the idea of a vector. If a scalar is considered a zero dimensional quantity, and a vector is a one dimensional quantity, then a bivector can be thought of as two dimensional. Bivectors...
- (sums of 2-blades also are bivectors, but may not be simple), given by the wedge product of two vectors a and b: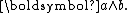
- A 3-blade of grade 3 is a trivector, that is, a wedge product of three vectors, a, b and c:
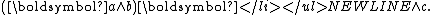
- A k-blade is a blade of gradeGraded algebraIn mathematics, in particular abstract algebra, a graded algebra is an algebra over a field with an extra piece of structure, known as a gradation ....
k. - The highest grade element in a space is called the pseudoscalarPseudoscalarIn physics, a pseudoscalar is a quantity that behaves like a scalar, except that it changes sign under a parity inversion such as improper rotations while a true scalar does not.The prototypical example of a pseudoscalar is the scalar triple product...
. - In a space of dimension n, the blade of grade n−1 is called a pseudovectorPseudovectorIn physics and mathematics, a pseudovector is a quantity that transforms like a vector under a proper rotation, but gains an additional sign flip under an improper rotation such as a reflection. Geometrically it is the opposite, of equal magnitude but in the opposite direction, of its mirror image...
.
In a n-dimensional spaces, there are blades of grade zero through n. A vector space of finite dimension n is related to a pseudoscalar of grade n.
Examples
For example, in 2-dimensional space scalars are described as 0-blades, vectors are 1-blades, and area elements are 2-blades known as pseudoscalarPseudoscalarIn physics, a pseudoscalar is a quantity that behaves like a scalar, except that it changes sign under a parity inversion such as improper rotations while a true scalar does not.The prototypical example of a pseudoscalar is the scalar triple product...
s, in that they are one-dimensional objects distinct from regular scalars.
In three-dimensional space, 0-blades are again scalars and 1-blades are three-dimensional vectors, but in three-dimensions, areas have an orientation, so while 2-blades are area elements, they are oriented. 3-blades (trivectors) represent volume elements and in three-dimensional space, these are scalar-like – i.e., 3-blades in three-dimensions form a one-dimensional vector space.
General references
- A Lasenby, J Lasenby & R Wareham (2004) A covariant approach to geometry using geometric algebra Technical Report. University of Cambridge Department of Engineering, Cambridge, UK.
External links
- A Geometric Algebra Primer, especially for computer scientists.
- A k-blade is a blade of grade

