
Heisenberg model (quantum)
Encyclopedia
The Heisenberg model is a statistical mechanical
model
used in the study of critical point
s and phase transition
s of magnetic systems, in which the spin
of the magnetic systems are treated quantum mechanically
. In the prototypical Ising model
, defined on a d-dimensional lattice, at each lattice site, a spin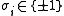 represents a microscopic magnetic dipole to which the magnetic moment is either up or down.
represents a microscopic magnetic dipole to which the magnetic moment is either up or down.
or the subchapter "quantum-mechanical origin of magnetism" in the article on magnetism), the dominant coupling between two dipoles may cause nearest-neighbors to have lowest energy when they are aligned. Under this assumption (so that magnetic interactions only occur between adjacent dipoles) the Hamiltonian
can be written in the form
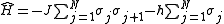
for a 1-dimensional model consisting of N dipoles, represented by classical vectors (or "spins") σj, subject to the periodic boundary condition .
.
The Heisenberg model is a more realistic model in that it treats the spins quantum-mechanically, by replacing the spin by a quantum operator (Pauli spin-1/2 matrices
at spin 1/2), and the coupling constants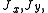 and
and 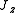 . As such in 3-dimensions, the Hamiltonian is given by
. As such in 3-dimensions, the Hamiltonian is given by
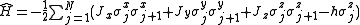
where the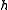 on the right-hand side indicates the external magnetic field
on the right-hand side indicates the external magnetic field
, with periodic boundary conditions, and at spin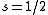 , spin matrices given by
, spin matrices given by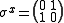
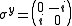
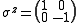
The Hamiltonian then acts upon the tensor product
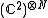 , of dimension
, of dimension 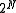 . The objective is to determine the spectrum of the Hamiltonian, from which the partition function
. The objective is to determine the spectrum of the Hamiltonian, from which the partition function
can be calculated, from which the thermodynamics
of the system can be studied. The most widely known type of Heisenberg model is the Heisenberg XXZ model, which occurs in the case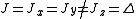 . The spin 1/2 Heisenberg model in one dimension may be solved exactly using the Bethe ansatz
. The spin 1/2 Heisenberg model in one dimension may be solved exactly using the Bethe ansatz
, while other approaches do so without Bethe ansatz.
The physics of the Heisenberg model strongly depends on the sign of the coupling constant
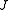 and the dimension of the space. For positive
and the dimension of the space. For positive 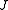 the ground state is always ferromagnetic
the ground state is always ferromagnetic
. At negative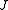 the ground state is antiferromagnetic
the ground state is antiferromagnetic
in two and three dimensions, it is from this ground state that the Hubbard model
is given. In one dimension the nature of correlations in the antiferromagnetic Heisenberg model depends on the spin of the magnetic dipoles. If the spin is integer then only short range order is present.
A system of half-integer spins exhibits quasi-long range order.
Statistical mechanics
Statistical mechanics or statistical thermodynamicsThe terms statistical mechanics and statistical thermodynamics are used interchangeably...
model
Mathematical model
A mathematical model is a description of a system using mathematical concepts and language. The process of developing a mathematical model is termed mathematical modeling. Mathematical models are used not only in the natural sciences and engineering disciplines A mathematical model is a...
used in the study of critical point
Critical point (thermodynamics)
In physical chemistry, thermodynamics, chemistry and condensed matter physics, a critical point, also called a critical state, specifies the conditions at which a phase boundary ceases to exist...
s and phase transition
Phase transition
A phase transition is the transformation of a thermodynamic system from one phase or state of matter to another.A phase of a thermodynamic system and the states of matter have uniform physical properties....
s of magnetic systems, in which the spin
Spin (physics)
In quantum mechanics and particle physics, spin is a fundamental characteristic property of elementary particles, composite particles , and atomic nuclei.It is worth noting that the intrinsic property of subatomic particles called spin and discussed in this article, is related in some small ways,...
of the magnetic systems are treated quantum mechanically
Quantum mechanics
Quantum mechanics, also known as quantum physics or quantum theory, is a branch of physics providing a mathematical description of much of the dual particle-like and wave-like behavior and interactions of energy and matter. It departs from classical mechanics primarily at the atomic and subatomic...
. In the prototypical Ising model
Ising model
The Ising model is a mathematical model of ferromagnetism in statistical mechanics. The model consists of discrete variables called spins that can be in one of two states . The spins are arranged in a graph , and each spin interacts with its nearest neighbors...
, defined on a d-dimensional lattice, at each lattice site, a spin
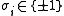 represents a microscopic magnetic dipole to which the magnetic moment is either up or down.
represents a microscopic magnetic dipole to which the magnetic moment is either up or down.Overview
For quantum mechanical reasons (see exchange interactionExchange interaction
In physics, the exchange interaction is a quantum mechanical effect without classical analog which increases or decreases the expectation value of the energy or distance between two or more identical particles when their wave functions overlap...
or the subchapter "quantum-mechanical origin of magnetism" in the article on magnetism), the dominant coupling between two dipoles may cause nearest-neighbors to have lowest energy when they are aligned. Under this assumption (so that magnetic interactions only occur between adjacent dipoles) the Hamiltonian
Hamiltonian (quantum mechanics)
In quantum mechanics, the Hamiltonian H, also Ȟ or Ĥ, is the operator corresponding to the total energy of the system. Its spectrum is the set of possible outcomes when one measures the total energy of a system...
can be written in the form
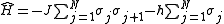
for a 1-dimensional model consisting of N dipoles, represented by classical vectors (or "spins") σj, subject to the periodic boundary condition
 .
. The Heisenberg model is a more realistic model in that it treats the spins quantum-mechanically, by replacing the spin by a quantum operator (Pauli spin-1/2 matrices
Pauli matrices
The Pauli matrices are a set of three 2 × 2 complex matrices which are Hermitian and unitary. Usually indicated by the Greek letter "sigma" , they are occasionally denoted with a "tau" when used in connection with isospin symmetries...
at spin 1/2), and the coupling constants
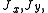 and
and 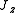 . As such in 3-dimensions, the Hamiltonian is given by
. As such in 3-dimensions, the Hamiltonian is given by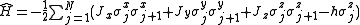
where the
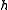 on the right-hand side indicates the external magnetic field
on the right-hand side indicates the external magnetic fieldMagnetic field
A magnetic field is a mathematical description of the magnetic influence of electric currents and magnetic materials. The magnetic field at any given point is specified by both a direction and a magnitude ; as such it is a vector field.Technically, a magnetic field is a pseudo vector;...
, with periodic boundary conditions, and at spin
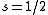 , spin matrices given by
, spin matrices given by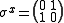
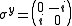
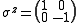
The Hamiltonian then acts upon the tensor product
Tensor product
In mathematics, the tensor product, denoted by ⊗, may be applied in different contexts to vectors, matrices, tensors, vector spaces, algebras, topological vector spaces, and modules, among many other structures or objects. In each case the significance of the symbol is the same: the most general...
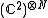 , of dimension
, of dimension 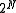 . The objective is to determine the spectrum of the Hamiltonian, from which the partition function
. The objective is to determine the spectrum of the Hamiltonian, from which the partition functionPartition function (statistical mechanics)
Partition functions describe the statistical properties of a system in thermodynamic equilibrium. It is a function of temperature and other parameters, such as the volume enclosing a gas...
can be calculated, from which the thermodynamics
Thermodynamics
Thermodynamics is a physical science that studies the effects on material bodies, and on radiation in regions of space, of transfer of heat and of work done on or by the bodies or radiation...
of the system can be studied. The most widely known type of Heisenberg model is the Heisenberg XXZ model, which occurs in the case
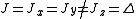 . The spin 1/2 Heisenberg model in one dimension may be solved exactly using the Bethe ansatz
. The spin 1/2 Heisenberg model in one dimension may be solved exactly using the Bethe ansatzBethe ansatz
In physics, the Bethe ansatz is a method for finding the exact solutions of certain one-dimensional quantum many-body models. It was invented by Hans Bethe in 1931 to find the exact eigenvalues and eigenvectors of the one-dimensional antiferromagnetic Heisenberg model Hamiltonian...
, while other approaches do so without Bethe ansatz.
The physics of the Heisenberg model strongly depends on the sign of the coupling constant
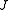 and the dimension of the space. For positive
and the dimension of the space. For positive 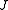 the ground state is always ferromagnetic
the ground state is always ferromagneticFerromagnetism
Ferromagnetism is the basic mechanism by which certain materials form permanent magnets, or are attracted to magnets. In physics, several different types of magnetism are distinguished...
. At negative
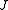 the ground state is antiferromagnetic
the ground state is antiferromagneticAntiferromagnetism
In materials that exhibit antiferromagnetism, the magnetic moments of atoms or molecules, usuallyrelated to the spins of electrons, align in a regular pattern with neighboring spins pointing in opposite directions. This is, like ferromagnetism and ferrimagnetism, a manifestation of ordered magnetism...
in two and three dimensions, it is from this ground state that the Hubbard model
Hubbard model
The Hubbard model is an approximate model used, especially in solid state physics, to describe the transition between conducting and insulating systems...
is given. In one dimension the nature of correlations in the antiferromagnetic Heisenberg model depends on the spin of the magnetic dipoles. If the spin is integer then only short range order is present.
A system of half-integer spins exhibits quasi-long range order.
Applications
- Another important object is entanglement entropy.One way to describe it is to subdivide the unique ground state into a block (several sequential spins) and the environment (the rest of the ground state). The entropy of the block can be considered as entanglement entropy. At zero temperature in the critical region (in thermodynamic limit) it scales logarithmically with the size of the block. As the temperature increases the logarithmic dependence changes into a linear function.For large temperature linear dependence follows from the second law of thermodynamics.
See also
- Bethe ansatzBethe ansatzIn physics, the Bethe ansatz is a method for finding the exact solutions of certain one-dimensional quantum many-body models. It was invented by Hans Bethe in 1931 to find the exact eigenvalues and eigenvectors of the one-dimensional antiferromagnetic Heisenberg model Hamiltonian...
- Classical Heisenberg model
- Dmrg of Heisenberg modelDmrg of Heisenberg modelThis example presents the infinite DMRG algorithm. It is about S=1 antiferromagnetic Heisenberg chain, but the recipe can be applied for every translationally invariant one-dimensional lattice...
- Ising modelIsing modelThe Ising model is a mathematical model of ferromagnetism in statistical mechanics. The model consists of discrete variables called spins that can be in one of two states . The spins are arranged in a graph , and each spin interacts with its nearest neighbors...
- Quantum rotor modelQuantum rotor modelThe quantum rotor model is a mathematical model for a quantum system. It can be visualized as an array of rotating electrons which behave as rigid rotors that interact through short-range dipole-dipole magnetic forces originating from their magnetic dipole moments...
- t-J modelT-J modelThe t-J model was first derived in 1977 from the Hubbard model by Józef Spałek. The model describes strongly correlated electron systems. It is used to calculate high temperature superconductivity states in doped antiferromagnets.The t-J Hamiltonian is:...
- J1 J2 modelJ1 J2 modelThe J1-J2 model is a quantum spin model like the Heisenberg model but also includes a term for the interaction between next-nearest neighbor spins.-Hamiltonian:-See also:*Spin model*Heisenberg model *Hubbard model*t-J model*Majumdar-Ghosh Model...
- Majumdar-Ghosh ModelMajumdar-Ghosh ModelThe Majumdar-Ghosh model is an extension of the one-dimensional quantum Heisenberg spin model in which an extra interaction is added coupling spins two lattice spacings apart such that second-neighbor coupling half as strong the first. It is therefore a special case of the J1 J2 model...
- AKLT ModelAKLT ModelThe AKLT model is an extension of the one-dimensional quantum Heisenberg spin model. The proposal and exact solution of this model by Affleck, Lieb, Kennedy and Tasaki provided crucial insight into the physics of the spin 1 Heisenberg chain...

