Quantum rotor model
Encyclopedia
The quantum rotor model is a mathematical model for a quantum system. It can be visualized as an array of rotating electrons which behave as rigid rotor
s that interact through short-range dipole-dipole magnetic forces originating from their magnetic dipole moments (neglecting Coulomb forces). The model differs from similar spin-models such as the Ising model
and the Heisenberg model
in that it includes a term analogous to kinetic energy
.
Although elementary quantum rotors do not exist in nature, the model can describe effective degrees of freedom for a system of sufficiently small number of closely coupled electrons in low-energy states.
Suppose the n-dimensional position (orientation) vector of the model at a given site
is 
. Then, we can define rotor momentum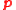 
by the commutation relation of components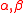 
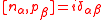
However, it is found convenient to use rotor angular momentum
operators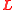
defined (in 3 dimensions) by components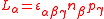 
Then, the magnetic interactions between the quantum rotors, and thus their energy states, can be described by the following Hamiltonian
:
where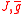
are constants.. The interaction sum is taken over nearest neighbors, as indicated by the angle brackets. For very small and very large 
, the Hamiltonian predicts two distinct configurations (ground state
s), namely "magnetically" ordered rotors and disordered or "paramagnetic
" rotors, respectively.
The interactions between the quantum rotors can be described by another (equivalent) Hamiltonian, which treats the rotors not as magnetic moments but as local electric currents.
symmetry, and hence the corresponding continuous symmetry breaking
in the magnetically ordered state. In a system with two layers of Heisenberg spins
and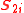 
, the rotor model approximates the low-energy states of a Heisenberg antiferromagnet, with the Hamiltonian
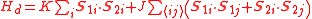
using the correspondence
The particular case of quantum rotor model which has the O(2) symmetry can be used to describe a superconducting array of Josephson junctions or the behavior of bosons in optical lattice
s. Another specific case of O(3) symmetry is equivalent to a system of two layers (bilayer) of a quantum Heisenberg antiferromagnet
; it can also describe double-layer quantum Hall ferromagnets. It can also be shown that the phase transition
for the two dimensional rotor model has the same universality class
as that of antiferromagnetic Heisenberg spin models.
Rigid rotor
The rigid rotor is a mechanical model that is used to explain rotating systems.An arbitrary rigid rotor is a 3-dimensional rigid object, such as a top. To orient such an object in space three angles are required. A special rigid rotor is the linear rotor which isa 2-dimensional object, requiring...
s that interact through short-range dipole-dipole magnetic forces originating from their magnetic dipole moments (neglecting Coulomb forces). The model differs from similar spin-models such as the Ising model
Ising model
The Ising model is a mathematical model of ferromagnetism in statistical mechanics. The model consists of discrete variables called spins that can be in one of two states . The spins are arranged in a graph , and each spin interacts with its nearest neighbors...
and the Heisenberg model
Heisenberg model (quantum)
The Heisenberg model is a statistical mechanical model used in the study of critical points and phase transitions of magnetic systems, in which the spin of the magnetic systems are treated quantum mechanically...
in that it includes a term analogous to kinetic energy
Kinetic energy
The kinetic energy of an object is the energy which it possesses due to its motion.It is defined as the work needed to accelerate a body of a given mass from rest to its stated velocity. Having gained this energy during its acceleration, the body maintains this kinetic energy unless its speed changes...
.
Although elementary quantum rotors do not exist in nature, the model can describe effective degrees of freedom for a system of sufficiently small number of closely coupled electrons in low-energy states.
Suppose the n-dimensional position (orientation) vector of the model at a given site
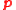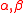
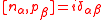
is . Then, we can define rotor momentum by the commutation relation of components However, it is found convenient to use rotor angular momentum
Angular momentum
In physics, angular momentum, moment of momentum, or rotational momentum is a conserved vector quantity that can be used to describe the overall state of a physical system...
operators
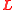defined (in 3 dimensions) by components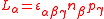 Then, the magnetic interactions between the quantum rotors, and thus their energy states, can be described by the following Hamiltonian
Hamiltonian
Hamiltonian may refer toIn mathematics :* Hamiltonian system* Hamiltonian path, in graph theory** Hamiltonian cycle, a special case of a Hamiltonian path* Hamiltonian group, in group theory* Hamiltonian...
:
where
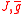are constants.. The interaction sum is taken over nearest neighbors, as indicated by the angle brackets. For very small and very large , the Hamiltonian predicts two distinct configurations (ground stateGround state
The ground state of a quantum mechanical system is its lowest-energy state; the energy of the ground state is known as the zero-point energy of the system. An excited state is any state with energy greater than the ground state...
s), namely "magnetically" ordered rotors and disordered or "paramagnetic
Paramagnetism
Paramagnetism is a form of magnetism whereby the paramagnetic material is only attracted when in the presence of an externally applied magnetic field. In contrast with this, diamagnetic materials are repulsive when placed in a magnetic field...
" rotors, respectively.
The interactions between the quantum rotors can be described by another (equivalent) Hamiltonian, which treats the rotors not as magnetic moments but as local electric currents.
Properties
One of the important features of the rotor model is the continuous O(N)Orthogonal group
In mathematics, the orthogonal group of degree n over a field F is the group of n × n orthogonal matrices with entries from F, with the group operation of matrix multiplication...
symmetry, and hence the corresponding continuous symmetry breaking
Symmetry breaking
Symmetry breaking in physics describes a phenomenon where small fluctuations acting on a system which is crossing a critical point decide the system's fate, by determining which branch of a bifurcation is taken. To an outside observer unaware of the fluctuations , the choice will appear arbitrary...
in the magnetically ordered state. In a system with two layers of Heisenberg spins
Heisenberg model (quantum)
The Heisenberg model is a statistical mechanical model used in the study of critical points and phase transitions of magnetic systems, in which the spin of the magnetic systems are treated quantum mechanically...
and 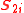, the rotor model approximates the low-energy states of a Heisenberg antiferromagnet, with the Hamiltonian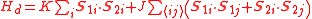using the correspondence
The particular case of quantum rotor model which has the O(2) symmetry can be used to describe a superconducting array of Josephson junctions or the behavior of bosons in optical lattice
Optical lattice
An optical lattice is formed by the interference of counter-propagating laser beams, creating a spatially periodic polarization pattern. The resulting periodic potential may trap neutral atoms via the Stark shift. Atoms are cooled and congregate in the locations of potential minima...
s. Another specific case of O(3) symmetry is equivalent to a system of two layers (bilayer) of a quantum Heisenberg antiferromagnet
Heisenberg model (quantum)
The Heisenberg model is a statistical mechanical model used in the study of critical points and phase transitions of magnetic systems, in which the spin of the magnetic systems are treated quantum mechanically...
; it can also describe double-layer quantum Hall ferromagnets. It can also be shown that the phase transition
Phase transition
A phase transition is the transformation of a thermodynamic system from one phase or state of matter to another.A phase of a thermodynamic system and the states of matter have uniform physical properties....
for the two dimensional rotor model has the same universality class
Renormalization group
In theoretical physics, the renormalization group refers to a mathematical apparatus that allows systematic investigation of the changes of a physical system as viewed at different distance scales...
as that of antiferromagnetic Heisenberg spin models.