Rigid rotor
Encyclopedia
The rigid rotor is a mechanical model that is used to explain rotating systems.
An arbitrary rigid rotor is a 3-dimensional rigid object, such as a top
. To orient such an object in space three angles are required. A special rigid rotor is the linear rotor which is
a 2-dimensional object, requiring two angles to describe its orientation. An example of a linear rotor
is a diatomic molecule
. More general molecules like water (asymmetric rotor),
ammonia (symmetric rotor), or methane (spherical rotor) are 3-dimensional, see classification of molecules.
The fixed distance between the two masses and the values of the masses are the only characteristics of the rigid model. However, for many actual diatomics this model is too restrictive since distances are usually not completely fixed. Corrections on the rigid model can be made to compensate for small variations in the distance. Even in such a case the rigid rotor model is a useful point of departure (zeroth-order model).
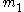and 
(with reduced mass
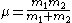) each at a distance 
. The rotor is rigid if 
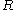is independent of time.
The kinematics of a linear rigid rotor is usually described by means of spherical polar coordinates, which form a coordinate system of R3. In the physics convention the coordinates are the co-latitude (zenith) angle
, the longitudinal (azimuth) angle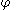 
and the distance 
.
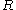The angles specify the orientation of the rotor in space.
The kinetic energy
of the linear rigid rotor is given by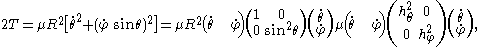
where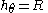
and 
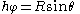are
scale (or Lamé) factors.
Scale factors are of importance for quantum mechanical applications since they
enter the Laplacian expressed in curvilinear coordinates.
In the case at hand (constant
)
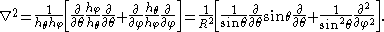
The classical Hamiltonian function of the linear rigid rotor is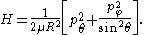
to predict the rotational energy of a diatomic
molecule. The rotational energy depends on the moment of inertia
for the system,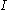
. In the center of mass
reference frame, the moment of inertia is equal to:
where
is the reduced mass
of the molecule and
is the distance between the two atoms.
According to quantum mechanics
, the energy levels of a system can be determined by solving the Schrödinger equation
:
where
is the wave function and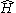 
is the energy (Hamiltonian
) operator. For the rigid rotor in a field-free space, the energy operator corresponds to the kinetic energy
of the system:
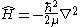
where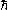
is Planck's constant divided by 
and 
is the Laplacian. The Laplacian is given above in terms of spherical polar coordinates. The energy operator written in terms of these coordinates is:
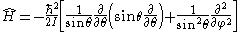
This operator appears also in the Schrödinger equation of the hydrogen atom after the radial part
is separated off. The eigenvalue equation becomes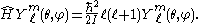
The symbol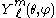
represents a set of functions known as the spherical harmonic
s. Note that the energy does not depend on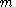
. The energy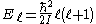
is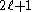
-fold degenerate: the functions with fixed 
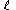and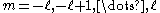 
have the same energy.
Introducing the rotational constant B, we write,
In the units of reciprocal length
the rotational constant is,
with c the speed of light. If cgs units are used for h, c, and I,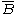
is expressed
in wave numbers
, cm−1, a unit that is often used for rotational-vibrational spectroscopy.
The rotational constant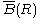
depends on the distance 
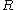. Often one writes 
where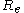 
is the equilibrium value
of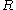
(the value for which the interaction energy of the atoms in the rotor has a minimum).
A typical rotational spectrum consists of a series of peaks that correspond to transitions between levels with different values of the angular momentum quantum number
(
). Consequently, rotational peaks
appear at energies corresponding to an integer multiple of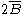
.
electronic transition. Pure rotational transitions, in which the vibronic (= vibrational plus electronic) wave function does not change, occur in the microwave
region of the electromagnetic spectrum.
Typically, rotational transitions can only be observed when the angular momentum quantum number
changes by 1 (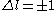
). This selection rule arises from a first-order perturbation theory approximation of the time-dependent Schrödinger equation
. According to this treatment, rotational transitions can only be observed when one or more
components of the dipole operator
have a non-vanishing transition moment. If z is the direction of the electric field component of the incoming em wave, the transition moment is,
A transition occurs if this integral is non-zero. By separating the rotational part of the molecular wavefunction from the vibronic
part, one can show that this means that the molecule must have a permanent dipole moment
.
After integration over the vibronic coordinates
the following rotational part of the transition moment remains,
Here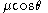
is the z component of the permanent dipole moment. The moment 
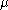is the vibronically averaged component of the dipole operator. Only the component of the permanent dipole along the axis of a heteronuclear molecule is non-vanishing.
By the use of the orthogonality of the spherical harmonics
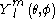
it is possible to determine which values of
, 
, 
, and 
will result in nonzero values for the dipole transition moment integral. This constraint results in the observed selection rules for the rigid rotor:
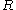) are not completely fixed; the bond between the atoms stretches out as the molecule rotates faster (higher values of the rotational quantum number
). This effect can be accounted for by introducing a correction factor known as the centrifugal distortion constant 
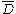(bars on top of various quantities indicate that these quantities are expressed in cm−1):
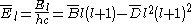
where
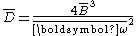
is the fundamental vibrational frequency of the bond (in cm-1). This frequency is related to the reduced mass and the force constant (bond strength) of the molecule according to
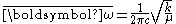
The non-rigid rotor is an acceptably accurate model for diatomic molecules but is still somewhat imperfect. This is because, although the model does account for bond stretching due to rotation, it ignores any bond stretching due to vibrational energy in the bond (anharmonicity in the potential).
of arbitrary shape with its center of mass
fixed (or in uniform rectilinear motion) in field-free space R3, so that its energy consists only of rotational kinetic energy (and possibly constant translational energy that can be ignored). A rigid body can be (partially) characterized by the three eigenvalues of its moment of inertia tensor, which are real nonnegative values known as principal moments of inertia.
In microwave spectroscopy—the spectroscopy based on rotational transitions—one usually classifies molecules (seen as rigid rotors) as follows:
This classification depends on the relative magnitudes of the principal moments of inertia.
of the kinematics of a rigid rotor. In molecular physics Euler angles
are used almost exclusively. In quantum mechanical applications it is advantageous to use Euler
angles in a convention that is a simple extension of the physical convention of spherical polar coordinates
.
The first step is the attachment of a right-handed orthonormal frame (3-dimensional system of orthogonal axes) to the rotor (a body-fixed frame) . This frame can be attached arbitrarily to the body, but often one uses the principal axes frame—the normalized eigenvectors of the inertia tensor, which always can be chosen orthonormal, since the tensor is Hermitian. When the rotor possesses a symmetry-axis, it usually coincides with one of the principal axes. It is convenient to choose
as body-fixed z-axis the highest-order symmetry axis.
One starts by aligning the body-fixed frame with a space-fixed frame
(laboratory axes), so that the body-fixed x, y, and z axes coincide with the space-fixed X, Y, and Z axis. Secondly, the body and its frame are rotated actively over a positive angle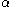
around the z-axis (by the right-hand rule), which moves the 
- to the 
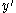-axis. Thirdly, one rotates the body and its frame over a positive angle 
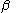around the 
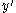-axis. The z-axis of the body-fixed frame has after these two rotations the longitudinal angle 
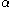(commonly designated by 
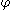) and the colatitude angle 
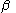(commonly designated by 
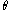), both with respect to the space-fixed frame. If the rotor were cylindrical symmetric around its z-axis, like the linear rigid rotor, its orientation in space would be unambiguously specified at this point.
If the body lacks cylinder (axial) symmetry, a last rotation around its z-axis (which has polar coordinates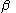
and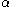 
) is necessary to specify its orientation completely. Traditionally the last rotation angle is called 
.
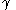The convention for Euler angles described here is known as the
convention; it can be shown (in the same manner as in this article) that it is equivalent to the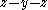 
convention in which the order of rotations is reversed.
The total matrix of the three consecutive rotations is the product
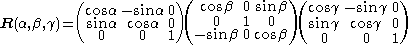
Let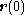
be the coordinate vector of an arbitrary point 
in the body with respect to the body-fixed frame. The elements of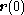 
are the 'body-fixed coordinates' of 
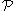. Initially 
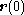is also the space-fixed coordinate vector of 
.
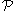Upon rotation of the body, the body-fixed coordinates of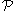
do not change, but the space-fixed coordinate vector of 
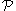becomes,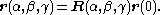
In particular, if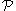
is initially on the space-fixed Z-axis, it has
the space-fixed coordinates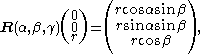
which shows the correspondence with the spherical polar coordinates
(in the physical convention).
Knowledge of the Euler angles as function of time t and the initial coordinates
determine the kinematics of the rigid rotor.
of an object that rotates around one axis.
It will be assumed from here on that the body-fixed frame is a principal axes frame; it diagonalizes the instantaneous inertia tensor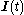
(expressed with respect to the space-fixed frame), i.e.,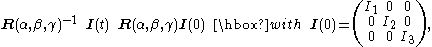
where the Euler angles are time-dependent and in fact determine the time dependence of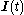
by the inverse of this equation. This notation implies
that at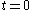
the Euler angles are zero, so that at 
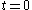the body-fixed frame coincides with the space-fixed frame.
The classical kinetic energy T of the rigid rotor can be expressed in different ways:
Since each of these forms has its use and can be found in textbooks we will present all of them.
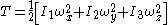
with
The vector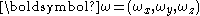
contains the components of the angular velocity
of the rotor expressed with respect to the body-fixed frame. It can be shown that
is not the time derivative of any vector, in contrast to the usual definition of velocity. The dots over the time-dependent Euler angles indicate time derivatives
.
The angular velocity satisfies equations of motion known as Euler's equations (with zero applied torque, since by assumption the rotor is in field-free space).
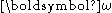into T gives
the kinetic energy in Lagrange form
(as a function of the time derivatives of the Euler angles). In matrix-vector notation,
where
is the metric tensor expressed in Euler angles—a non-orthogonal system of curvilinear coordinates
—
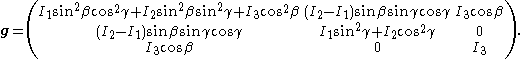
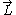of the rigid rotor. This vector is a conserved (time-independent) quantity.
With respect to the body-fixed frame it has the components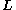
, which can be shown to
be related to the angular velocity,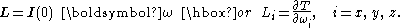
Since the body-fixed frame moves (depends on time) these components are not time independent. If we were
to represent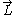
with respect to the stationary space-fixed frame, we would
find time independent expressions for its components.
The kinetic energy is given by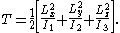
of the kinetic energy is written in terms
of generalized momenta
where it is used that the
is symmetric.
In Hamilton form the kinetic energy is,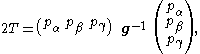
with the inverse metric tensor given by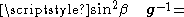
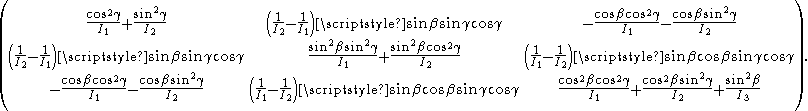
This inverse tensor is needed to obtain the Laplace-Beltrami operator
, which (multiplied
by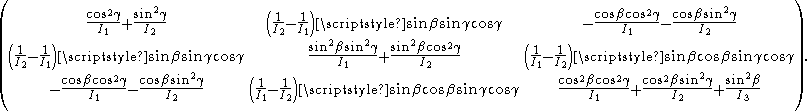
) gives the quantum mechanical energy operator
of the rigid rotor.
The classical Hamiltonian given above can be rewritten to the following expression, which is needed in the phase integral
arising in the classical statistical mechanics of rigid rotors,
by operators that give first derivatives with respect to its canonically conjugate variables (positions). Thus,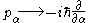
and similarly for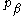
and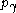 
. It is remarkable that this rule replaces the fairly complicated function 
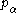of all three Euler angles, time derivatives of Euler angles, and inertia moments (characterizing the rigid rotor) by a simple differential operator that does not depend on time or inertia moments and differentiates to one Euler angle only.
The quantization rule is sufficient to obtain the operators
that correspond with the classical angular momenta. There are two kinds: space-fixed and body-fixed
angular momentum operators. Both are vector operators, i.e., both have three components
that transform as vector components among themselves upon rotation of the space-fixed and the body-fixed frame, respectively. The explicit form of the rigid rotor angular momentum operators is
given here
(but beware, they must be multiplied with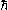
). The body-fixed angular momentum operators are written
as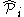
. They satisfy anomalous commutation relations.
The quantization rule is not sufficient to obtain the kinetic energy operator from
the classical Hamiltonian. Since classically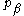
commutes with 
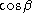and 
and the inverses of these functions, the position
of these trigonometric functions in the classical Hamiltonian is arbitrary. After
quantization the commutation does no longer hold and the order of operators and functions in the Hamiltonian (energy operator) becomes a point of concern. Podolsky proposed in 1928 that the Laplace-Beltrami operator
(times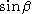
) has the appropriate form for the quantum mechanical kinetic
energy operator. This operator has the general form (summation convention: sum over repeated indices—in this case over the three Euler angles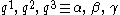
):
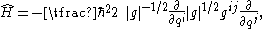
where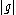
is the determinant of the g-tensor: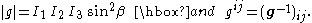
Given the inverse of the metric tensor above, the explicit form of the kinetic energy operator in terms of Euler angles follows by simple substitution. (Note: The corresponding eigenvalue equation
gives the Schrödinger equation
for the rigid rotor in the form that it was
solved for the first time by Kronig and Rabi (for the special case of the symmetric rotor). This is one of the few cases where the Schrödinger equation can be solved analytically. All these cases were solved within a year of the formulation of the Schrödinger equation.)
Nowadays it is common to proceed as follows. It can be shown that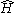
can be expressed in body-fixed angular momentum operators (in this proof one must carefully
commute differential operators with trigonometric functions). The result has the same appearance
as the classical formula expressed in body-fixed coordinates,
The action of the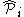
on the Wigner D-matrix is simple. In particular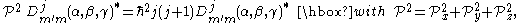
so that the Schrödinger equation for the spherical rotor (
)
is solved with the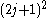
degenerate energy equal to 
.
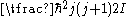The symmetric top (= symmetric rotor) is characterized by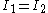
. It is
a prolate (cigar shaped) top if
. In the latter
case we write the Hamiltonian as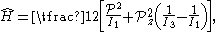
and use that
Hence
The eigenvalue
is 
-fold degenerate, for all eigenfunctions
with
have the same eigenvalue. The energies with |k| > 0 are
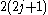-fold degenerate. This exact solution of the
Schrödinger equation of the symmetric top was first found in 1927.
The asymmetric top problem (
) is not exactly soluble.
An arbitrary rigid rotor is a 3-dimensional rigid object, such as a top
Top
A top is a toy that can be spun on an axis, balancing on a point. This motion is produced in the most simple forms of top by twirling the stem using the fingers. More sophisticated tops are spun by by holding the axis firmly while pulling a string or twisting a stick or pushing an auger as shown...
. To orient such an object in space three angles are required. A special rigid rotor is the linear rotor which is
a 2-dimensional object, requiring two angles to describe its orientation. An example of a linear rotor
is a diatomic molecule
Molecule
A molecule is an electrically neutral group of at least two atoms held together by covalent chemical bonds. Molecules are distinguished from ions by their electrical charge...
. More general molecules like water (asymmetric rotor),
ammonia (symmetric rotor), or methane (spherical rotor) are 3-dimensional, see classification of molecules.
The linear rotor
The linear rigid rotor model consists of two point masses located at fixed distances from their center of mass.The fixed distance between the two masses and the values of the masses are the only characteristics of the rigid model. However, for many actual diatomics this model is too restrictive since distances are usually not completely fixed. Corrections on the rigid model can be made to compensate for small variations in the distance. Even in such a case the rigid rotor model is a useful point of departure (zeroth-order model).
The classical linear rigid rotor
The classical linear rotor consists of two point masses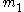 and (with reduced mass
Reduced mass
Reduced mass is the "effective" inertial mass appearing in the two-body problem of Newtonian mechanics. This is a quantity with the unit of mass, which allows the two-body problem to be solved as if it were a one-body problem. Note however that the mass determining the gravitational force is not...
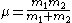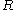) each at a distance . The rotor is rigid if is independent of time.The kinematics of a linear rigid rotor is usually described by means of spherical polar coordinates, which form a coordinate system of R3. In the physics convention the coordinates are the co-latitude (zenith) angle
, the longitudinal (azimuth) angle 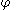and the distance 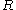.The angles specify the orientation of the rotor in space.
The kinetic energy
of the linear rigid rotor is given by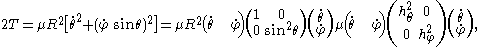where
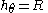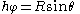and arescale (or Lamé) factors.
Scale factors are of importance for quantum mechanical applications since they
enter the Laplacian expressed in curvilinear coordinates.
In the case at hand (constant
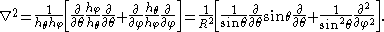
)The classical Hamiltonian function of the linear rigid rotor is
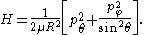
The quantum mechanical linear rigid rotor
The linear rigid rotor model can be used in quantum mechanicsQuantum mechanics
Quantum mechanics, also known as quantum physics or quantum theory, is a branch of physics providing a mathematical description of much of the dual particle-like and wave-like behavior and interactions of energy and matter. It departs from classical mechanics primarily at the atomic and subatomic...
to predict the rotational energy of a diatomic
Diatomic
Diatomic molecules are molecules composed only of two atoms, of either the same or different chemical elements. The prefix di- means two in Greek. Common diatomic molecules are hydrogen , nitrogen , oxygen , and carbon monoxide . Seven elements exist in the diatomic state in the liquid and solid...
molecule. The rotational energy depends on the moment of inertia
Moment of inertia
In classical mechanics, moment of inertia, also called mass moment of inertia, rotational inertia, polar moment of inertia of mass, or the angular mass, is a measure of an object's resistance to changes to its rotation. It is the inertia of a rotating body with respect to its rotation...
for the system,
. In the center of massCenter of mass
In physics, the center of mass or barycenter of a system is the average location of all of its mass. In the case of a rigid body, the position of the center of mass is fixed in relation to the body...
reference frame, the moment of inertia is equal to:
where
is the reduced massReduced mass
Reduced mass is the "effective" inertial mass appearing in the two-body problem of Newtonian mechanics. This is a quantity with the unit of mass, which allows the two-body problem to be solved as if it were a one-body problem. Note however that the mass determining the gravitational force is not...
of the molecule and
is the distance between the two atoms.According to quantum mechanics
Quantum mechanics
Quantum mechanics, also known as quantum physics or quantum theory, is a branch of physics providing a mathematical description of much of the dual particle-like and wave-like behavior and interactions of energy and matter. It departs from classical mechanics primarily at the atomic and subatomic...
, the energy levels of a system can be determined by solving the Schrödinger equation
Schrödinger equation
The Schrödinger equation was formulated in 1926 by Austrian physicist Erwin Schrödinger. Used in physics , it is an equation that describes how the quantum state of a physical system changes in time....
:
where
is the wave function and 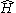is the energy (HamiltonianHamiltonian (quantum mechanics)
In quantum mechanics, the Hamiltonian H, also Ȟ or Ĥ, is the operator corresponding to the total energy of the system. Its spectrum is the set of possible outcomes when one measures the total energy of a system...
) operator. For the rigid rotor in a field-free space, the energy operator corresponds to the kinetic energy
Kinetic energy
The kinetic energy of an object is the energy which it possesses due to its motion.It is defined as the work needed to accelerate a body of a given mass from rest to its stated velocity. Having gained this energy during its acceleration, the body maintains this kinetic energy unless its speed changes...
of the system:
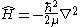
where
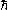is Planck's constant divided by and is the Laplacian. The Laplacian is given above in terms of spherical polar coordinates. The energy operator written in terms of these coordinates is: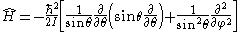This operator appears also in the Schrödinger equation of the hydrogen atom after the radial part
is separated off. The eigenvalue equation becomes
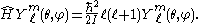
The symbol
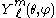represents a set of functions known as the spherical harmonicSpherical Harmonic
Spherical Harmonic is a science fiction novel from the Saga of the Skolian Empire by Catherine Asaro. It tells the story of Dyhianna Selei , the Ruby Pharaoh of the Skolian Imperialate, as she strives to reform her government and reunite her family in the aftermath of a devastating interstellar...
s. Note that the energy does not depend on
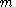. The energy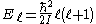is
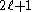-fold degenerate: the functions with fixe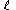d and 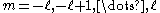have the same energy.Introducing the rotational constant B, we write,
In the units of reciprocal length
Reciprocal length
Reciprocal length or inverse length is a measurement used in several branches of science and mathematics. As the reciprocal of length, common units used for this measurement include the reciprocal metre or inverse metre , the reciprocal centimetre or inverse centimetre , and, in optics, the...
the rotational constant is,
with c the speed of light. If cgs units are used for h, c, and I,
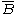is expressedin wave numbers
Wavenumber
In the physical sciences, the wavenumber is a property of a wave, its spatial frequency, that is proportional to the reciprocal of the wavelength. It is also the magnitude of the wave vector...
, cm−1, a unit that is often used for rotational-vibrational spectroscopy.
The rotational constant
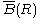depends on the distance 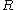. Often one writes where 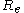is the equilibrium valueof
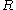(the value for which the interaction energy of the atoms in the rotor has a minimum).A typical rotational spectrum consists of a series of peaks that correspond to transitions between levels with different values of the angular momentum quantum number
Quantum number
Quantum numbers describe values of conserved quantities in the dynamics of the quantum system. Perhaps the most peculiar aspect of quantum mechanics is the quantization of observable quantities. This is distinguished from classical mechanics where the values can range continuously...
(
). Consequently, rotational peaksRotational spectroscopy
Rotational spectroscopy or microwave spectroscopy studies the absorption and emission of electromagnetic radiation by molecules associated with a corresponding change in the rotational quantum number of the molecule...
appear at energies corresponding to an integer multiple of
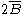.Selection rules
Rotational transitions of a molecule occur when the molecule absorbs a photon [a particle of a quantized electromagnetic (em) field]. Depending on the energy of the photon (i.e., the wavelength of the em field) this transition may be seen as a sideband of a vibrational and/orelectronic transition. Pure rotational transitions, in which the vibronic (= vibrational plus electronic) wave function does not change, occur in the microwave
Microwave
Microwaves, a subset of radio waves, have wavelengths ranging from as long as one meter to as short as one millimeter, or equivalently, with frequencies between 300 MHz and 300 GHz. This broad definition includes both UHF and EHF , and various sources use different boundaries...
region of the electromagnetic spectrum.
Typically, rotational transitions can only be observed when the angular momentum quantum number
Quantum number
Quantum numbers describe values of conserved quantities in the dynamics of the quantum system. Perhaps the most peculiar aspect of quantum mechanics is the quantization of observable quantities. This is distinguished from classical mechanics where the values can range continuously...
changes by 1 (
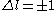). This selection rule arises from a first-order perturbation theory approximation of the time-dependent Schrödinger equationSchrödinger equation
The Schrödinger equation was formulated in 1926 by Austrian physicist Erwin Schrödinger. Used in physics , it is an equation that describes how the quantum state of a physical system changes in time....
. According to this treatment, rotational transitions can only be observed when one or more
components of the dipole operator
have a non-vanishing transition moment. If z is the direction of the electric field component of the incoming em wave, the transition moment is,
A transition occurs if this integral is non-zero. By separating the rotational part of the molecular wavefunction from the vibronic
part, one can show that this means that the molecule must have a permanent dipole moment
Electric dipole moment
In physics, the electric dipole moment is a measure of the separation of positive and negative electrical charges in a system of charges, that is, a measure of the charge system's overall polarity with SI units of Coulomb-meter...
.
After integration over the vibronic coordinates
the following rotational part of the transition moment remains,
Here
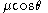is the z component of the permanent dipole moment. The moment 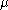is the vibronically averaged component of the dipole operator. Only the component of the permanent dipole along the axis of a heteronuclear molecule is non-vanishing.By the use of the orthogonality of the spherical harmonics
Spherical harmonics
In mathematics, spherical harmonics are the angular portion of a set of solutions to Laplace's equation. Represented in a system of spherical coordinates, Laplace's spherical harmonics Y_\ell^m are a specific set of spherical harmonics that forms an orthogonal system, first introduced by Pierre...
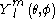
it is possible to determine which values of
, , , and will result in nonzero values for the dipole transition moment integral. This constraint results in the observed selection rules for the rigid rotor:Non-rigid linear rotor
The rigid rotor is commonly used to describe the rotational energy of diatomic molecules but it is not a completely accurate description of such molecules. This is because molecular bonds (and therefore the interatomic distance) are not completely fixed; the bond between the atoms stretches out as the molecule rotates faster (higher values of the rotational quantum numberQuantum number
Quantum numbers describe values of conserved quantities in the dynamics of the quantum system. Perhaps the most peculiar aspect of quantum mechanics is the quantization of observable quantities. This is distinguished from classical mechanics where the values can range continuously...
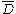). This effect can be accounted for by introducing a correction factor known as the centrifugal distortion constant (bars on top of various quantities indicate that these quantities are expressed in cm−1):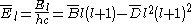where
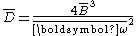
is the fundamental vibrational frequency of the bond (in cm-1). This frequency is related to the reduced mass and the force constant (bond strength) of the molecule according to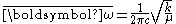The non-rigid rotor is an acceptably accurate model for diatomic molecules but is still somewhat imperfect. This is because, although the model does account for bond stretching due to rotation, it ignores any bond stretching due to vibrational energy in the bond (anharmonicity in the potential).
Arbitrarily shaped rigid rotor
An arbitrarily shaped rigid rotor is a rigid bodyRigid body
In physics, a rigid body is an idealization of a solid body of finite size in which deformation is neglected. In other words, the distance between any two given points of a rigid body remains constant in time regardless of external forces exerted on it...
of arbitrary shape with its center of mass
Center of mass
In physics, the center of mass or barycenter of a system is the average location of all of its mass. In the case of a rigid body, the position of the center of mass is fixed in relation to the body...
fixed (or in uniform rectilinear motion) in field-free space R3, so that its energy consists only of rotational kinetic energy (and possibly constant translational energy that can be ignored). A rigid body can be (partially) characterized by the three eigenvalues of its moment of inertia tensor, which are real nonnegative values known as principal moments of inertia.
In microwave spectroscopy—the spectroscopy based on rotational transitions—one usually classifies molecules (seen as rigid rotors) as follows:
- spherical rotors
- symmetric rotors
- oblate symmetric rotors
- prolate symmetric rotors
- asymmetric rotors
This classification depends on the relative magnitudes of the principal moments of inertia.
Coordinates of the rigid rotor
Different branches of physics and engineering use different coordinates for the descriptionof the kinematics of a rigid rotor. In molecular physics Euler angles
Euler angles
The Euler angles are three angles introduced by Leonhard Euler to describe the orientation of a rigid body. To describe such an orientation in 3-dimensional Euclidean space three parameters are required...
are used almost exclusively. In quantum mechanical applications it is advantageous to use Euler
angles in a convention that is a simple extension of the physical convention of spherical polar coordinates
Spherical coordinate system
In mathematics, a spherical coordinate system is a coordinate system for three-dimensional space where the position of a point is specified by three numbers: the radial distance of that point from a fixed origin, its inclination angle measured from a fixed zenith direction, and the azimuth angle of...
.
The first step is the attachment of a right-handed orthonormal frame (3-dimensional system of orthogonal axes) to the rotor (a body-fixed frame) . This frame can be attached arbitrarily to the body, but often one uses the principal axes frame—the normalized eigenvectors of the inertia tensor, which always can be chosen orthonormal, since the tensor is Hermitian. When the rotor possesses a symmetry-axis, it usually coincides with one of the principal axes. It is convenient to choose
as body-fixed z-axis the highest-order symmetry axis.
One starts by aligning the body-fixed frame with a space-fixed frame
(laboratory axes), so that the body-fixed x, y, and z axes coincide with the space-fixed X, Y, and Z axis. Secondly, the body and its frame are rotated actively over a positive angle
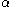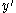around the z-axis (by the right-hand rule), which moves the - to the -axis. Thirdly, one rotates the body and its frame over a positive angle 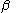around the 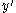-axis. The z-axis of the body-fixed frame has after these two rotations the longitudinal angle 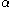(commonly designated by 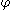) and the colatitude angle 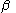(commonly designated by 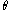), both with respect to the space-fixed frame. If the rotor were cylindrical symmetric around its z-axis, like the linear rigid rotor, its orientation in space would be unambiguously specified at this point.If the body lacks cylinder (axial) symmetry, a last rotation around its z-axis (which has polar coordinates
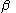and 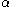) is necessary to specify its orientation completely. Traditionally the last rotation angle is called 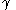.The convention for Euler angles described here is known as the
convention; it can be shown (in the same manner as in this article) that it is equivalent to the 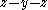convention in which the order of rotations is reversed.The total matrix of the three consecutive rotations is the product
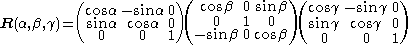
Let
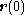be the coordinate vector of an arbitrary point in the body with respect to the body-fixed frame. The elements of 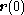are the 'body-fixed coordinates' of 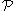. Initially 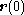is also the space-fixed coordinate vector of 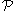.Upon rotation of the body, the body-fixed coordinates of
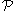do not change, but the space-fixed coordinate vector of 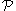becomes,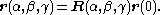In particular, if
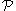is initially on the space-fixed Z-axis, it hasthe space-fixed coordinates
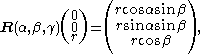
which shows the correspondence with the spherical polar coordinates
Spherical coordinate system
In mathematics, a spherical coordinate system is a coordinate system for three-dimensional space where the position of a point is specified by three numbers: the radial distance of that point from a fixed origin, its inclination angle measured from a fixed zenith direction, and the azimuth angle of...
(in the physical convention).
Knowledge of the Euler angles as function of time t and the initial coordinates
determine the kinematics of the rigid rotor.Classical kinetic energy
The following text forms a generalization of the well-known special case of the rotational energyRotational energy
The rotational energy or angular kinetic energy is the kinetic energy due to the rotation of an object and is part of its total kinetic energy...
of an object that rotates around one axis.
It will be assumed from here on that the body-fixed frame is a principal axes frame; it diagonalizes the instantaneous inertia tensor
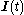(expressed with respect to the space-fixed frame), i.e.,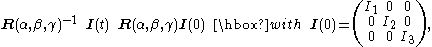where the Euler angles are time-dependent and in fact determine the time dependence of
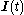by the inverse of this equation. This notation impliesthat at
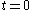the Euler angles are zero, so that at 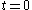the body-fixed frame coincides with the space-fixed frame.The classical kinetic energy T of the rigid rotor can be expressed in different ways:
- as a function of angular velocity
- in Lagrangian form
- as a function of angular momentum
- in Hamiltonian form.
Since each of these forms has its use and can be found in textbooks we will present all of them.
Angular velocity form
As a function of angular velocity T reads,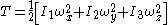with
The vector
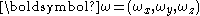contains the components of the angular velocityAngular velocity
In physics, the angular velocity is a vector quantity which specifies the angular speed of an object and the axis about which the object is rotating. The SI unit of angular velocity is radians per second, although it may be measured in other units such as degrees per second, revolutions per...
of the rotor expressed with respect to the body-fixed frame. It can be shown that
is not the time derivative of any vector, in contrast to the usual definition of velocity. The dots over the time-dependent Euler angles indicate time derivativesNewton's notation for differentiation
Newton's notation for differentiation, or dot notation, uses a dot placed over a function name to denote the time derivative of that function. Newton referred to this as a fluxion.Isaac Newton's notation is mainly used in mechanics...
.
The angular velocity satisfies equations of motion known as Euler's equations (with zero applied torque, since by assumption the rotor is in field-free space).
Lagrange form
Backsubstitution of the expression of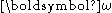 into T givesthe kinetic energy in Lagrange form
Lagrangian mechanics
Lagrangian mechanics is a re-formulation of classical mechanics that combines conservation of momentum with conservation of energy. It was introduced by the Italian-French mathematician Joseph-Louis Lagrange in 1788....
(as a function of the time derivatives of the Euler angles). In matrix-vector notation,
where
is the metric tensor expressed in Euler angles—a non-orthogonal system of curvilinear coordinatesCurvilinear coordinates
Curvilinear coordinates are a coordinate system for Euclidean space in which the coordinate lines may be curved. These coordinates may be derived from a set of Cartesian coordinates by using a transformation that is locally invertible at each point. This means that one can convert a point given...
—
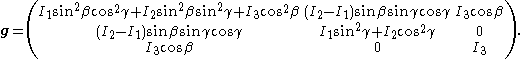
Angular momentum form
Often the kinetic energy is written as a function of the angular momentum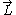 of the rigid rotor. This vector is a conserved (time-independent) quantity.With respect to the body-fixed frame it has the components
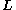, which can be shown tobe related to the angular velocity,
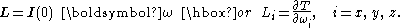
Since the body-fixed frame moves (depends on time) these components are not time independent. If we were
to represent
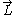with respect to the stationary space-fixed frame, we wouldfind time independent expressions for its components.
The kinetic energy is given by
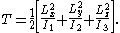
Hamilton form
The Hamilton formHamiltonian mechanics
Hamiltonian mechanics is a reformulation of classical mechanics that was introduced in 1833 by Irish mathematician William Rowan Hamilton.It arose from Lagrangian mechanics, a previous reformulation of classical mechanics introduced by Joseph Louis Lagrange in 1788, but can be formulated without...
of the kinetic energy is written in terms
of generalized momenta
where it is used that the
is symmetric.In Hamilton form the kinetic energy is,
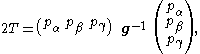
with the inverse metric tensor given by
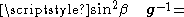
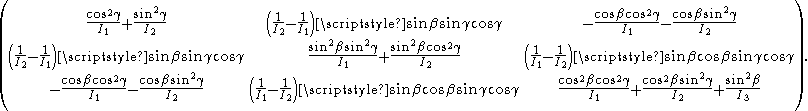
This inverse tensor is needed to obtain the Laplace-Beltrami operator
Laplace-Beltrami operator
In differential geometry, the Laplace operator, named after Pierre-Simon Laplace, can be generalized to operate on functions defined on surfaces in Euclidean space and, more generally, on Riemannian and pseudo-Riemannian manifolds. This more general operator goes by the name Laplace–Beltrami...
, which (multiplied
by
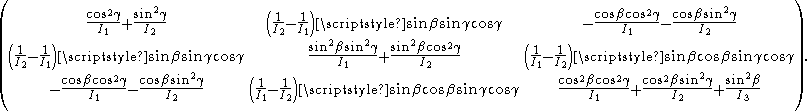) gives the quantum mechanical energy operatorof the rigid rotor.
The classical Hamiltonian given above can be rewritten to the following expression, which is needed in the phase integral
arising in the classical statistical mechanics of rigid rotors,
Quantum mechanical rigid rotor
As usual quantization is performed by the replacement of the generalized momentaby operators that give first derivatives with respect to its canonically conjugate variables (positions). Thus,
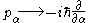
and similarly for
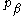and 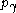. It is remarkable that this rule replaces the fairly complicated function 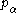of all three Euler angles, time derivatives of Euler angles, and inertia moments (characterizing the rigid rotor) by a simple differential operator that does not depend on time or inertia moments and differentiates to one Euler angle only.The quantization rule is sufficient to obtain the operators
that correspond with the classical angular momenta. There are two kinds: space-fixed and body-fixed
angular momentum operators. Both are vector operators, i.e., both have three components
that transform as vector components among themselves upon rotation of the space-fixed and the body-fixed frame, respectively. The explicit form of the rigid rotor angular momentum operators is
given here
Wigner D-matrix
The Wigner D-matrix is a matrix in an irreducible representation of the groups SU and SO. The complex conjugate of the D-matrix is an eigenfunction of the Hamiltonian of spherical and symmetric rigid rotors. The matrix was introduced in 1927 by Eugene Wigner.- Definition Wigner D-matrix :Let j_x,...
(but beware, they must be multiplied with
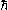). The body-fixed angular momentum operators are writtenas
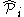. They satisfy anomalous commutation relations.The quantization rule is not sufficient to obtain the kinetic energy operator from
the classical Hamiltonian. Since classically
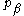commutes with 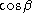and and the inverses of these functions, the positionof these trigonometric functions in the classical Hamiltonian is arbitrary. After
quantization the commutation does no longer hold and the order of operators and functions in the Hamiltonian (energy operator) becomes a point of concern. Podolsky proposed in 1928 that the Laplace-Beltrami operator
(times
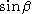) has the appropriate form for the quantum mechanical kineticenergy operator. This operator has the general form (summation convention: sum over repeated indices—in this case over the three Euler angles
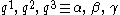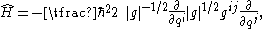
):where
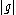is the determinant of the g-tensor: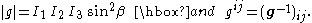Given the inverse of the metric tensor above, the explicit form of the kinetic energy operator in terms of Euler angles follows by simple substitution. (Note: The corresponding eigenvalue equation
gives the Schrödinger equation
Schrödinger equation
The Schrödinger equation was formulated in 1926 by Austrian physicist Erwin Schrödinger. Used in physics , it is an equation that describes how the quantum state of a physical system changes in time....
for the rigid rotor in the form that it was
solved for the first time by Kronig and Rabi (for the special case of the symmetric rotor). This is one of the few cases where the Schrödinger equation can be solved analytically. All these cases were solved within a year of the formulation of the Schrödinger equation.)
Nowadays it is common to proceed as follows. It can be shown that
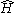
can be expressed in body-fixed angular momentum operators (in this proof one must carefully
commute differential operators with trigonometric functions). The result has the same appearance
as the classical formula expressed in body-fixed coordinates,
The action of the
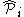on the Wigner D-matrix is simple. In particular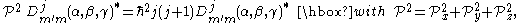so that the Schrödinger equation for the spherical rotor (
)is solved with the
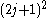degenerate energy equal to 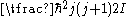.The symmetric top (= symmetric rotor) is characterized by
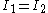. It isa prolate (cigar shaped) top if
. In the lattercase we write the Hamiltonian as
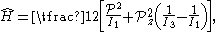
and use that
Hence
The eigenvalue
is -fold degenerate, for all eigenfunctionswith
have the same eigenvalue. The energies with |k| > 0 are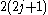-fold degenerate. This exact solution of theSchrödinger equation of the symmetric top was first found in 1927.
The asymmetric top problem (
) is not exactly soluble.See also
- Balancing machineBalancing MachineA balancing machine is a measuring tool used for balancing rotating machine parts such as rotors for electric motors, fans, turbines, disc brakes, disc drives, propellers and pumps. The machine usually consists of two rigid pedestals, with suspension and bearings on top supporting a mounting...
- GyroscopeGyroscopeA gyroscope is a device for measuring or maintaining orientation, based on the principles of angular momentum. In essence, a mechanical gyroscope is a spinning wheel or disk whose axle is free to take any orientation...
- Infrared spectroscopyInfrared spectroscopyInfrared spectroscopy is the spectroscopy that deals with the infrared region of the electromagnetic spectrum, that is light with a longer wavelength and lower frequency than visible light. It covers a range of techniques, mostly based on absorption spectroscopy. As with all spectroscopic...
- Rigid bodyRigid bodyIn physics, a rigid body is an idealization of a solid body of finite size in which deformation is neglected. In other words, the distance between any two given points of a rigid body remains constant in time regardless of external forces exerted on it...
- Rotational spectroscopyRotational spectroscopyRotational spectroscopy or microwave spectroscopy studies the absorption and emission of electromagnetic radiation by molecules associated with a corresponding change in the rotational quantum number of the molecule...
- SpectroscopySpectroscopySpectroscopy is the study of the interaction between matter and radiated energy. Historically, spectroscopy originated through the study of visible light dispersed according to its wavelength, e.g., by a prism. Later the concept was expanded greatly to comprise any interaction with radiative...
- Vibrational spectroscopy
- Quantum rotor modelQuantum rotor modelThe quantum rotor model is a mathematical model for a quantum system. It can be visualized as an array of rotating electrons which behave as rigid rotors that interact through short-range dipole-dipole magnetic forces originating from their magnetic dipole moments...