Rotational spectroscopy
Encyclopedia
Rotational spectroscopy or microwave spectroscopy studies the absorption and emission of electromagnetic radiation
(typically in the microwave
region of the electromagnetic spectrum
) by molecules associated with a corresponding change in the rotational quantum number
of the molecule. The use of microwaves in spectroscopy essentially became possible due to the development of microwave technology for RADAR
during World War II
. Rotational spectroscopy is practical only in the gas
phase
where the rotational motion
is quantized
. In solids or liquids the rotational motion is usually quenched due to collisions.
Rotational spectrum from a molecule (to first order) requires that the molecule have a dipole moment and that there be a difference between its center of charge
and its center of mass
, or equivalently a separation between two unlike charges. It is this dipole moment that enables the electric field
of the light
(microwave
) to exert a torque
on the molecule, causing it to rotate more quickly (in excitation
) or slowly (in de-excitation). Homonuclear
diatomic molecules such as dioxygen (O2)
, dihydrogen (H2)
, etc. do not have a dipole moment and, hence, no purely rotational spectrum. However, electronic excitations can lead to asymmetric charge distributions and thus provide a net dipole moment to the molecule. Under such circumstances, these molecules will exhibit a rotational spectrum.
Among the diatomic molecules
, carbon monoxide (CO)
has one of the simplest rotational spectra. As for tri-atomic molecules, hydrogen cyanide (HC≡N) has a simple rotational spectrum for a linear molecule and hydrogen isocyanide (HN=C:)
for a non-linear molecule. As the number of atoms increases, the spectrum becomes more complex, as lines, due to different transitions, start overlapping.
the free rotation of a molecule is quantized, that is the rotational energy
and the angular momentum
can take only certain fixed values; what these values are is related simply to the moment of inertia
,
, of the molecule. In general, for any molecule, there are three moments of inertia: 
, 
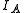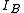and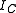 
about three mutually orthogonal axes A, B, and C with the origin at the center of mass
of the system. Linear molecules are a special case because one of the moments of inertia (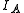
, the moment of inertia along molecular axis) is negligible (i.e., 
).
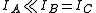The general convention is to define the axes such that the axis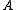
has the smallest moment of inertia, the axis 
axis is the next smallest and so on such that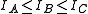 
. (A rarely used convention defines the 
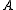axis along a symmetric axis of the molecule, if one exists. To avoid confusion, this article uses the prior convention.) The particular pattern of energy level
s (and, hence, of transitions in the rotational spectrum) for a molecule is determined by its symmetry. A convenient way to look at the molecules is to divide them into four different classes (based on the symmetry of their structure). These are linear molecules, symmetric tops, spherical tops, and asymmetric tops. (Equivalently, many authors use the word "rotor" instead of "top".)
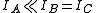. For most of the purposes, 
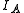is taken to be zero. For a linear molecule, the separation of lines in the rotational spectrum can be related directly to the moment of inertia of the molecule, and, for a molecule of known atomic masses, can be used to determine the bond length
s (structure) directly. For diatomic molecules
, this process is trivial, and can be made from a single measurement of the rotational spectrum. For linear molecules with more atoms, rather more work is required, and it is necessary to measure molecules in which more than one isotope of each atom have been substituted (effectively this gives rise to a set of simultaneous equations that can be solved for the bond length
s).
Examples of linear molecules: dioxygen (O=O)
, carbon monoxide (O≡C*)
, hydroxy radical (OH)
, carbon dioxide (O=C=O)
, hydrogen cyanide (HC≡N), carbonyl sulfide (O=C=S)
, chloroethyne (HC≡CCl), acetylene (HC≡CH)
and Prolate symmetric tops (rugby football, or cigar shaped) with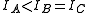 
. The spectra look rather different, and are instantly recognizable. As with linear molecules, the structure of symmetric tops (bond length
s and bond angles
) can be deduced from their spectra.
Examples of symmetric tops:
).
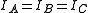Examples of spherical tops: phosphorus tetramer (P4), carbon tetrachloride (CCl4)
, methane (CH4)
, ammonium ion (NH4+)
, sulfur hexafluoride (SF6)
Examples of asymmetric tops: anthracene (C14H10)
, water (H2O), nitrogen dioxide (NO2)
These molecules have two degenerate modes of rotation (
, 
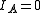). Since we cannot distinguish between the two modes, we need only one rotational quantum number (
) to describe the rotational motion of the molecule.
The rotational energy levels (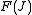
) of the molecule based on rigid rotor
model can be expressed as,
where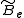
is the rotational constant of the molecule and is related to the moment of inertia of the molecule 
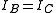by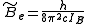
(in wavenumber scale).
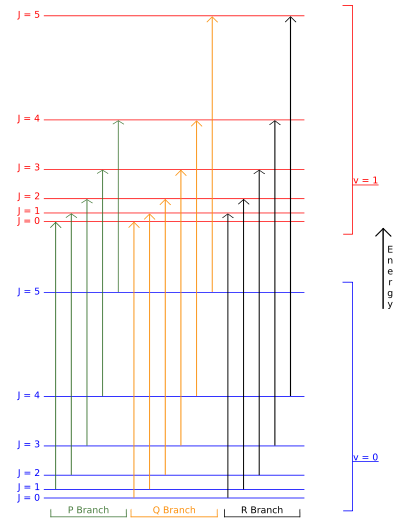
Selection rules dictate that during emission or absorption the rotational quantum number has to change by unity; i.e.,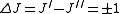
. Thus, the locations of the lines in a rotational spectrum will be given by
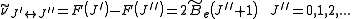
where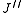
denotes the lower energy level and 
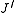denotes higher energy level involved in the transition. The height of the lines is determined by the distribution of the molecules in the different levels and the probability of transition between two energy levels.
We observe that, for a rigid rotor, the transition lines are equally spaced in the wavenumber space. However, this is not always the case, except for the rigid rotor model. For non-rigid rotor model, we need to consider changes in the moment of inertia of the molecule. Two primary reasons for this are
pulls the atoms apart. As a result, the moment of inertia of the molecule increases, thus decreasing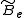
. To account for this a centrifugal distortion correction term is added to the rotational energy levels of the molecule.
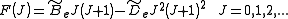
where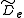
is the centrifugal distortion constant.
Therefore, the line spacing for the rotational mode changes to,
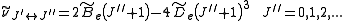
Further, there is a fictitious force
, Coriolis coupling
, between the vibrational motion of the nuclei in the rotating (non-inertial) frame. However, as long as the vibrational quantum number does not change (i.e., the molecule is in only one state of vibration), the effect of vibration on rotation is not important, because the time for vibration is much shorter than the time required for rotation. The Coriolis coupling is often negligible, too, if one is interested in low vibrational and rotational quantum numbers only.
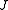) with the total angular momentum of the molecule and the other quantum number (
) with the angular momentum of the axis that has different moment of inertia (i.e., axis 
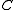for oblate symmetric top and axis 
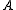for prolate symmetric tops). The rotational energy 
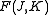of such a molecule, based on rigid rotor assumptions can be expressed in terms of the two previously defined rotational quantum numbers as follows
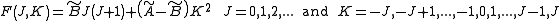
where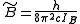
and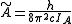 
for a prolate symmetric top molecule or
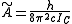for an oblate molecule.
Selection rule for these molecules provide the guidelines for possible transitions. Therefore,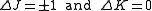
.
This is so because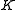
is associated with the axis about which the molecule is symmetric and, hence, has no net dipole moment in that direction. Thus, there is no interaction of this mode with the light particles (photons).
This gives the transition wavenumbers of
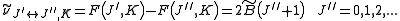
which is the same as in the case of a linear molecule.
In case of non-rigid rotors, the first order centrifugal distortion correction is given by
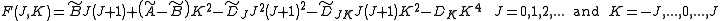
The suffixes on the centrifugal distortion constant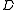
indicate the rotational mode involved and are not a function of the rotational quantum number. The location of the transition lines on a spectrum is given by
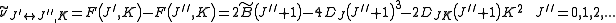
From the moments of inertia one can define an asymmetry parameter
as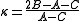
, which varies from -1 for a prolate symmetric top to 1 for an oblate symmetric top.
One can define a scaled rotational Hamiltonian
dependent on
and 
. The (symmetric) matrix representation of this Hamiltonian is banded, zero everywhere but the main diagonal and the second subdiagonal. The Hamiltonian can be formulated in six different settings, dependent on the mapping of the principal axes to lab axes and handedness. For the most asymmetric, right-handed representation, the diagonal elements are, for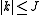 
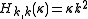
and the second off-diagonal elements (independent of
) are
.
Diagonalising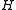
yields a set of 
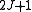scaled rotational energy levels 
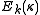. The rotational energy levels of the asymmetric rotor for total angular momentum 
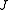are then given by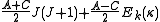
These interactions give rise to the characteristic energy levels that are probed in "magnetic resonance" spectroscopy such as NMR
and ESR, where they represent the "zero field splittings," which are always present.
can be used to experimentally study rotational spectra. Typical spectra at these wavelengths involve rovibrational excitation, i.e., excitation of both a vibrational and a rotational mode of a molecule.
In the past, microwave spectra were determined using a simple arrangement in which low-pressure gas was introduced to a section of waveguide between a microwave source (of variable frequency) and a microwave detector. The spectrum was obtained by sweeping the frequency of the source while detecting the intensity of the transmitted radiation. This experimental arrangement has a major difficulty related to the propagation of microwave radiation through waveguides. The physical size of the waveguide restricts the frequency of the radiation that can be transmitted through it. For a given waveguide size (such as X-band), there is a cutoff frequency, and microwave radiation with smaller frequencies (longer wavelengths) cannot be propagated through the waveguide. In addition, as the frequency is increased, additional modes of propagation become possible, which correspond to different velocities of the radiation propagating down the waveguide (this can be envisaged as the radiation bouncing down the guide, at different angles of reflection). the net result of these considerations is that each size of waveguide is useful only over a rather narrow range of frequencies and must be physically swapped out for a different size of waveguide once this frequency range is exceeded.
From 1980 onward, microwave spectra have often been obtained using Fourier Transform Microwave Spectroscopy - a technique developed by W. H. Flygare at the University of Illinois.
Within the last two years, a further development of Fourier Transform Microwave Spectroscopy has occurred, which may well introduce a new renaissance into microwave spectroscopy. This is the use of "Chirped Pulses" to provide an electromagnetic wave that has as its Fourier Transform a very wide range of microwave frequencies. (see University of Virginia, Chemistry Department website).
do not work very well for some of these molecules (especially the gases) and are not as precise. However, microwave spectroscopy is not useful for determining the structures of large molecules such as proteins.
Modern microwave spectrometers have very high resolution. When hyperfine structure can be observed, the technique can also provide information on the electronic structures of molecules.
Microwave spectroscopy is one of the principal means by which the constituents of the universe are determined from the earth. It is particularly useful for detecting molecules in the interstellar medium (ISM)
. One of the early surprises in interstellar chemistry came with the discovery of the existence in the ISM of long-chain carbon molecules. It was in attempting to research such molecules in the laboratory that Harry Kroto
was led to the laboratory of Rick Smalley
and Robert Curl
, where it was possible to vaporize carbon under enormous energy conditions. This collaborative experiment led to the discovery of C60, buckminsterfullerene
, which led to the award of the 1996 Nobel prize in chemistry to Kroto, Smalley and Curl.
Electromagnetic radiation
Electromagnetic radiation is a form of energy that exhibits wave-like behavior as it travels through space...
(typically in the microwave
Microwave
Microwaves, a subset of radio waves, have wavelengths ranging from as long as one meter to as short as one millimeter, or equivalently, with frequencies between 300 MHz and 300 GHz. This broad definition includes both UHF and EHF , and various sources use different boundaries...
region of the electromagnetic spectrum
Electromagnetic spectrum
The electromagnetic spectrum is the range of all possible frequencies of electromagnetic radiation. The "electromagnetic spectrum" of an object is the characteristic distribution of electromagnetic radiation emitted or absorbed by that particular object....
) by molecules associated with a corresponding change in the rotational quantum number
Quantum number
Quantum numbers describe values of conserved quantities in the dynamics of the quantum system. Perhaps the most peculiar aspect of quantum mechanics is the quantization of observable quantities. This is distinguished from classical mechanics where the values can range continuously...
of the molecule. The use of microwaves in spectroscopy essentially became possible due to the development of microwave technology for RADAR
Radar
Radar is an object-detection system which uses radio waves to determine the range, altitude, direction, or speed of objects. It can be used to detect aircraft, ships, spacecraft, guided missiles, motor vehicles, weather formations, and terrain. The radar dish or antenna transmits pulses of radio...
during World War II
World War II
World War II, or the Second World War , was a global conflict lasting from 1939 to 1945, involving most of the world's nations—including all of the great powers—eventually forming two opposing military alliances: the Allies and the Axis...
. Rotational spectroscopy is practical only in the gas
Gas
Gas is one of the three classical states of matter . Near absolute zero, a substance exists as a solid. As heat is added to this substance it melts into a liquid at its melting point , boils into a gas at its boiling point, and if heated high enough would enter a plasma state in which the electrons...
phase
Phase (matter)
In the physical sciences, a phase is a region of space , throughout which all physical properties of a material are essentially uniform. Examples of physical properties include density, index of refraction, and chemical composition...
where the rotational motion
Motion (physics)
In physics, motion is a change in position of an object with respect to time. Change in action is the result of an unbalanced force. Motion is typically described in terms of velocity, acceleration, displacement and time . An object's velocity cannot change unless it is acted upon by a force, as...
is quantized
Quantization (physics)
In physics, quantization is the process of explaining a classical understanding of physical phenomena in terms of a newer understanding known as "quantum mechanics". It is a procedure for constructing a quantum field theory starting from a classical field theory. This is a generalization of the...
. In solids or liquids the rotational motion is usually quenched due to collisions.
Rotational spectrum from a molecule (to first order) requires that the molecule have a dipole moment and that there be a difference between its center of charge
Electric charge
Electric charge is a physical property of matter that causes it to experience a force when near other electrically charged matter. Electric charge comes in two types, called positive and negative. Two positively charged substances, or objects, experience a mutual repulsive force, as do two...
and its center of mass
Center of mass
In physics, the center of mass or barycenter of a system is the average location of all of its mass. In the case of a rigid body, the position of the center of mass is fixed in relation to the body...
, or equivalently a separation between two unlike charges. It is this dipole moment that enables the electric field
Electric field
In physics, an electric field surrounds electrically charged particles and time-varying magnetic fields. The electric field depicts the force exerted on other electrically charged objects by the electrically charged particle the field is surrounding...
of the light
Light
Light or visible light is electromagnetic radiation that is visible to the human eye, and is responsible for the sense of sight. Visible light has wavelength in a range from about 380 nanometres to about 740 nm, with a frequency range of about 405 THz to 790 THz...
(microwave
Microwave
Microwaves, a subset of radio waves, have wavelengths ranging from as long as one meter to as short as one millimeter, or equivalently, with frequencies between 300 MHz and 300 GHz. This broad definition includes both UHF and EHF , and various sources use different boundaries...
) to exert a torque
Torque
Torque, moment or moment of force , is the tendency of a force to rotate an object about an axis, fulcrum, or pivot. Just as a force is a push or a pull, a torque can be thought of as a twist....
on the molecule, causing it to rotate more quickly (in excitation
Excited state
Excitation is an elevation in energy level above an arbitrary baseline energy state. In physics there is a specific technical definition for energy level which is often associated with an atom being excited to an excited state....
) or slowly (in de-excitation). Homonuclear
Homonuclear molecule
Homonuclear molecules, or homonuclear species, are molecules composed of only one type of element. Homonuclear molecules may consist of various numbers of atoms, depending on the element's properties. Some elements form molecules of more than one size. Noble gases rarely form bonds, so they only...
diatomic molecules such as dioxygen (O2)
Oxygen
Oxygen is the element with atomic number 8 and represented by the symbol O. Its name derives from the Greek roots ὀξύς and -γενής , because at the time of naming, it was mistakenly thought that all acids required oxygen in their composition...
, dihydrogen (H2)
Hydrogen
Hydrogen is the chemical element with atomic number 1. It is represented by the symbol H. With an average atomic weight of , hydrogen is the lightest and most abundant chemical element, constituting roughly 75% of the Universe's chemical elemental mass. Stars in the main sequence are mainly...
, etc. do not have a dipole moment and, hence, no purely rotational spectrum. However, electronic excitations can lead to asymmetric charge distributions and thus provide a net dipole moment to the molecule. Under such circumstances, these molecules will exhibit a rotational spectrum.
Among the diatomic molecules
Diatomic
Diatomic molecules are molecules composed only of two atoms, of either the same or different chemical elements. The prefix di- means two in Greek. Common diatomic molecules are hydrogen , nitrogen , oxygen , and carbon monoxide . Seven elements exist in the diatomic state in the liquid and solid...
, carbon monoxide (CO)
Carbon monoxide
Carbon monoxide , also called carbonous oxide, is a colorless, odorless, and tasteless gas that is slightly lighter than air. It is highly toxic to humans and animals in higher quantities, although it is also produced in normal animal metabolism in low quantities, and is thought to have some normal...
has one of the simplest rotational spectra. As for tri-atomic molecules, hydrogen cyanide (HC≡N) has a simple rotational spectrum for a linear molecule and hydrogen isocyanide (HN=C:)
Hydrogen isocyanide
Hydrogen isocyanide is a chemical with the molecular formula HNC. It is a minor tautomer of hydrogen cyanide, HCN). Its importance in the field of astrochemistry is linked to its ubiquity in the interstellar medium.- Nomenclature :...
for a non-linear molecule. As the number of atoms increases, the spectrum becomes more complex, as lines, due to different transitions, start overlapping.
Understanding the rotational spectrum
In quantum mechanicsQuantum mechanics
Quantum mechanics, also known as quantum physics or quantum theory, is a branch of physics providing a mathematical description of much of the dual particle-like and wave-like behavior and interactions of energy and matter. It departs from classical mechanics primarily at the atomic and subatomic...
the free rotation of a molecule is quantized, that is the rotational energy
Rotational energy
The rotational energy or angular kinetic energy is the kinetic energy due to the rotation of an object and is part of its total kinetic energy...
and the angular momentum
Angular momentum
In physics, angular momentum, moment of momentum, or rotational momentum is a conserved vector quantity that can be used to describe the overall state of a physical system...
can take only certain fixed values; what these values are is related simply to the moment of inertia
Moment of inertia
In classical mechanics, moment of inertia, also called mass moment of inertia, rotational inertia, polar moment of inertia of mass, or the angular mass, is a measure of an object's resistance to changes to its rotation. It is the inertia of a rotating body with respect to its rotation...
,
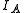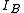, of the molecule. In general, for any molecule, there are three moments of inertia: , and 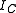about three mutually orthogonal axes A, B, and C with the origin at the center of massCenter of mass
In physics, the center of mass or barycenter of a system is the average location of all of its mass. In the case of a rigid body, the position of the center of mass is fixed in relation to the body...
of the system. Linear molecules are a special case because one of the moments of inertia (
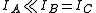, the moment of inertia along molecular axis) is negligible (i.e., ).The general convention is to define the axes such that the axis
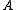has the smallest moment of inertia, the axis axis is the next smallest and so on such that 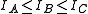. (A rarely used convention defines the 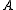axis along a symmetric axis of the molecule, if one exists. To avoid confusion, this article uses the prior convention.) The particular pattern of energy levelEnergy level
A quantum mechanical system or particle that is bound -- that is, confined spatially—can only take on certain discrete values of energy. This contrasts with classical particles, which can have any energy. These discrete values are called energy levels...
s (and, hence, of transitions in the rotational spectrum) for a molecule is determined by its symmetry. A convenient way to look at the molecules is to divide them into four different classes (based on the symmetry of their structure). These are linear molecules, symmetric tops, spherical tops, and asymmetric tops. (Equivalently, many authors use the word "rotor" instead of "top".)
Linear molecules
For a linear molecule the moments of inertia are related by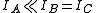. For most of the purposes, 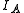is taken to be zero. For a linear molecule, the separation of lines in the rotational spectrum can be related directly to the moment of inertia of the molecule, and, for a molecule of known atomic masses, can be used to determine the bond lengthBond length
- Explanation :Bond length is related to bond order, when more electrons participate in bond formation the bond will get shorter. Bond length is also inversely related to bond strength and the bond dissociation energy, as a stronger bond will be shorter...
s (structure) directly. For diatomic molecules
Diatomic
Diatomic molecules are molecules composed only of two atoms, of either the same or different chemical elements. The prefix di- means two in Greek. Common diatomic molecules are hydrogen , nitrogen , oxygen , and carbon monoxide . Seven elements exist in the diatomic state in the liquid and solid...
, this process is trivial, and can be made from a single measurement of the rotational spectrum. For linear molecules with more atoms, rather more work is required, and it is necessary to measure molecules in which more than one isotope of each atom have been substituted (effectively this gives rise to a set of simultaneous equations that can be solved for the bond length
Bond length
- Explanation :Bond length is related to bond order, when more electrons participate in bond formation the bond will get shorter. Bond length is also inversely related to bond strength and the bond dissociation energy, as a stronger bond will be shorter...
s).
Examples of linear molecules: dioxygen (O=O)
Oxygen
Oxygen is the element with atomic number 8 and represented by the symbol O. Its name derives from the Greek roots ὀξύς and -γενής , because at the time of naming, it was mistakenly thought that all acids required oxygen in their composition...
, carbon monoxide (O≡C*)
Carbon monoxide
Carbon monoxide , also called carbonous oxide, is a colorless, odorless, and tasteless gas that is slightly lighter than air. It is highly toxic to humans and animals in higher quantities, although it is also produced in normal animal metabolism in low quantities, and is thought to have some normal...
, hydroxy radical (OH)
Hydroxyl radical
The hydroxyl radical, •OH, is the neutral form of the hydroxide ion . Hydroxyl radicals are highly reactive and consequently short-lived; however, they form an important part of radical chemistry. Most notably hydroxyl radicals are produced from the decomposition of hydroperoxides or, in...
, carbon dioxide (O=C=O)
Carbon dioxide
Carbon dioxide is a naturally occurring chemical compound composed of two oxygen atoms covalently bonded to a single carbon atom...
, hydrogen cyanide (HC≡N), carbonyl sulfide (O=C=S)
Carbonyl sulfide
Carbonyl sulfide is the chemical compound with the formula OCS. Commonly written as COS, it is a colourless flammable gas with an unpleasant odor. It is a linear molecule consisting of a carbonyl group double bonded to a sulfur atom...
, chloroethyne (HC≡CCl), acetylene (HC≡CH)
Acetylene
Acetylene is the chemical compound with the formula C2H2. It is a hydrocarbon and the simplest alkyne. This colorless gas is widely used as a fuel and a chemical building block. It is unstable in pure form and thus is usually handled as a solution.As an alkyne, acetylene is unsaturated because...
Symmetric tops
A symmetric top is a molecule in which two moments of inertia are the same. As a matter of historical convenience, spectroscopists divide molecules into two classes of symmetric tops, Oblate symmetric tops (saucer or disc shaped) with and Prolate symmetric tops (rugby football, or cigar shaped) with 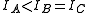. The spectra look rather different, and are instantly recognizable. As with linear molecules, the structure of symmetric tops (bond lengthBond length
- Explanation :Bond length is related to bond order, when more electrons participate in bond formation the bond will get shorter. Bond length is also inversely related to bond strength and the bond dissociation energy, as a stronger bond will be shorter...
s and bond angles
Molecular geometry
Molecular geometry or molecular structure is the three-dimensional arrangement of the atoms that constitute a molecule. It determines several properties of a substance including its reactivity, polarity, phase of matter, color, magnetism, and biological activity.- Molecular geometry determination...
) can be deduced from their spectra.
Examples of symmetric tops:
- Oblate: benzene (C6H6)BenzeneBenzene is an organic chemical compound. It is composed of 6 carbon atoms in a ring, with 1 hydrogen atom attached to each carbon atom, with the molecular formula C6H6....
, cyclobutadiene (C4H4)CyclobutadieneCyclobutadiene is the smallest [n]-annulene , an extremely unstable hydrocarbon having a lifetime shorter than five seconds in the free state. It has chemical formula 44 and a rectangular structure verified by infrared studies. This is in contrast to the square geometry predicted by simple Hückel...
, ammonia (NH3)AmmoniaAmmonia is a compound of nitrogen and hydrogen with the formula . It is a colourless gas with a characteristic pungent odour. Ammonia contributes significantly to the nutritional needs of terrestrial organisms by serving as a precursor to food and fertilizers. Ammonia, either directly or... - Prolate: chloromethane (CH3Cl)ChloromethaneChloromethane, also called methyl chloride, R-40 or HCC 40, is a chemical compound of the group of organic compounds called haloalkanes. It was once widely used as a refrigerant. It is a colorless extremely flammable gas with a minorly sweet odor, which is, however, detected at possibly toxic levels...
, propyne (CH3C≡CH)MethylacetyleneMethylacetylene is an alkyne with the chemical formula H3C≡CH. It is a component of MAPP gas along with its isomer 1,2-propadiene , which is commonly used in gas welding...
Spherical tops
A spherical top molecule can be considered as a special case of symmetric tops with equal moment of inertia about all three axes (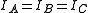).Examples of spherical tops: phosphorus tetramer (P4), carbon tetrachloride (CCl4)
Carbon tetrachloride
Carbon tetrachloride, also known by many other names is the organic compound with the formula CCl4. It was formerly widely used in fire extinguishers, as a precursor to refrigerants, and as a cleaning agent...
, methane (CH4)
Methane
Methane is a chemical compound with the chemical formula . It is the simplest alkane, the principal component of natural gas, and probably the most abundant organic compound on earth. The relative abundance of methane makes it an attractive fuel...
, ammonium ion (NH4+)
Ammonium
The ammonium cation is a positively charged polyatomic cation with the chemical formula NH. It is formed by the protonation of ammonia...
, sulfur hexafluoride (SF6)
Sulfur hexafluoride
Sulfur hexafluoride is an inorganic, colorless, odorless, and non-flammable greenhouse gas. has an octahedral geometry, consisting of six fluorine atoms attached to a central sulfur atom. It is a hypervalent molecule. Typical for a nonpolar gas, it is poorly soluble in water but soluble in...
Asymmetric tops
An asymmetric top occurs if all three moments of inertia are different. Most large molecules are asymmetric tops, even when they have a high degree of symmetry. In general, for such molecules, a simple interpretation of the spectrum is not normally possible. However, molecules have spectra similar to those of a linear molecule or a symmetric top, in which case the molecular structure may also be similar to that of a linear molecule or a symmetric top. For the most general case, however, all that can be done is to fit the spectra to three different moments of inertia. If the molecular formula is known, then educated guesses can be made of the possible structure, and, from this guessed structure, the moments of inertia can be calculated. If the calculated moments of inertia agree well with the measured moments of inertia, then the structure can be said to have been determined. For this approach to determining molecular structure, isotopic substitution is invaluable.Examples of asymmetric tops: anthracene (C14H10)
Anthracene
Anthracene is a solid polycyclic aromatic hydrocarbon consisting of three fused benzene rings. It is a component of coal-tar. Anthracene is used in the production of the red dye alizarin and other dyes...
, water (H2O), nitrogen dioxide (NO2)
Nitrogen dioxide
Nitrogen dioxide is the chemical compound with the formula it is one of several nitrogen oxides. is an intermediate in the industrial synthesis of nitric acid, millions of tons of which are produced each year. This reddish-brown toxic gas has a characteristic sharp, biting odor and is a prominent...
Linear molecules
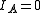, ). Since we cannot distinguish between the two modes, we need only one rotational quantum number () to describe the rotational motion of the molecule.The rotational energy levels (
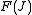) of the molecule based on rigid rotorRigid rotor
The rigid rotor is a mechanical model that is used to explain rotating systems.An arbitrary rigid rotor is a 3-dimensional rigid object, such as a top. To orient such an object in space three angles are required. A special rigid rotor is the linear rotor which isa 2-dimensional object, requiring...
model can be expressed as,
where
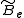is the rotational constant of the molecule and is related to the moment of inertia of the molecule 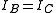by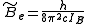(in wavenumber scale).
Selection rules dictate that during emission or absorption the rotational quantum number has to change by unity; i.e.,
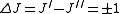. Thus, the locations of the lines in a rotational spectrum will be given by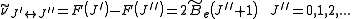where
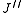denotes the lower energy level and 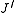denotes higher energy level involved in the transition. The height of the lines is determined by the distribution of the molecules in the different levels and the probability of transition between two energy levels.We observe that, for a rigid rotor, the transition lines are equally spaced in the wavenumber space. However, this is not always the case, except for the rigid rotor model. For non-rigid rotor model, we need to consider changes in the moment of inertia of the molecule. Two primary reasons for this are
Centrifugal distortion
When a molecule rotates, the centrifugal forceCentrifugal force
Centrifugal force can generally be any force directed outward relative to some origin. More particularly, in classical mechanics, the centrifugal force is an outward force which arises when describing the motion of objects in a rotating reference frame...
pulls the atoms apart. As a result, the moment of inertia of the molecule increases, thus decreasing
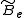. To account for this a centrifugal distortion correction term is added to the rotational energy levels of the molecule.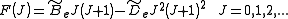where
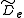is the centrifugal distortion constant.Therefore, the line spacing for the rotational mode changes to,
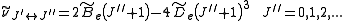
Effect of vibration on rotation
A molecule is always in vibration. As the molecule vibrates, its moment of inertia changes.Further, there is a fictitious force
Fictitious force
A fictitious force, also called a pseudo force, d'Alembert force or inertial force, is an apparent force that acts on all masses in a non-inertial frame of reference, such as a rotating reference frame....
, Coriolis coupling
Coriolis effect
In physics, the Coriolis effect is a deflection of moving objects when they are viewed in a rotating reference frame. In a reference frame with clockwise rotation, the deflection is to the left of the motion of the object; in one with counter-clockwise rotation, the deflection is to the right...
, between the vibrational motion of the nuclei in the rotating (non-inertial) frame. However, as long as the vibrational quantum number does not change (i.e., the molecule is in only one state of vibration), the effect of vibration on rotation is not important, because the time for vibration is much shorter than the time required for rotation. The Coriolis coupling is often negligible, too, if one is interested in low vibrational and rotational quantum numbers only.
Symmetric top
The rotational motion of a symmetric top molecule can be described by two independent rotational quantum numbers (since two axes have equal moments of inertia, the rotational motion about these axes requires only one rotational quantum number for complete description). 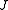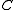Instead of defining the two rotational quantum numbers for two independent axes, we associate one of the quantum number () with the total angular momentum of the molecule and the other quantum number () with the angular momentum of the axis that has different moment of inertia (i.e., axis for oblate symmetric top and axis 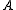for prolate symmetric tops). The rotational energy 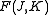of such a molecule, based on rigid rotor assumptions can be expressed in terms of the two previously defined rotational quantum numbers as follows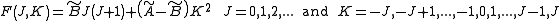where
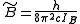and 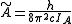for a prolate symmetric top molecule or 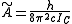for an oblate molecule.Selection rule for these molecules provide the guidelines for possible transitions. Therefore,
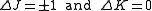.This is so because
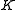is associated with the axis about which the molecule is symmetric and, hence, has no net dipole moment in that direction. Thus, there is no interaction of this mode with the light particles (photons).This gives the transition wavenumbers of
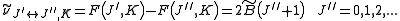
which is the same as in the case of a linear molecule.
In case of non-rigid rotors, the first order centrifugal distortion correction is given by
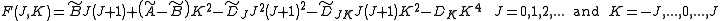
The suffixes on the centrifugal distortion constant
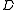indicate the rotational mode involved and are not a function of the rotational quantum number. The location of the transition lines on a spectrum is given by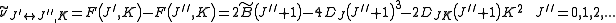Spherical top
Unlike other molecules, spherical top molecules have no net dipole moment, and, hence, they do not exhibit a pure rotational spectrum.Asymmetric top
The spectrum for these molecules usually involves many lines due to three different rotational modes and their combinations. The following analysis is valid for the general case and collapses to the various special cases described above in the appropriate limit.From the moments of inertia one can define an asymmetry parameter
as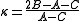, which varies from -1 for a prolate symmetric top to 1 for an oblate symmetric top.One can define a scaled rotational Hamiltonian
Hamiltonian (quantum mechanics)
In quantum mechanics, the Hamiltonian H, also Ȟ or Ĥ, is the operator corresponding to the total energy of the system. Its spectrum is the set of possible outcomes when one measures the total energy of a system...
dependent on
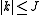
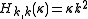
and . The (symmetric) matrix representation of this Hamiltonian is banded, zero everywhere but the main diagonal and the second subdiagonal. The Hamiltonian can be formulated in six different settings, dependent on the mapping of the principal axes to lab axes and handedness. For the most asymmetric, right-handed representation, the diagonal elements are, for and the second off-diagonal elements (independent of
) are.Diagonalising
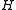yields a set of 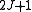scaled rotational energy levels 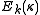. The rotational energy levels of the asymmetric rotor for total angular momentum 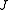are then given by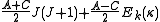Hyperfine interaction
In addition to the main structure that is observed in microwave spectra due to the rotational motion of the molecules, a whole host of further interactions are responsible for small details in the spectra, and the study of these details provides a very deep understanding of molecular quantum mechanics. The main interactions responsible for small changes in the spectra (additional splittings and shifts of lines) are due to magnetic and electrostatic interactions in the molecule. The particular strength of such interactions differs in different molecules, but, in general, the order of these effects (in decreasing significance) is:- electron spin - electron spin interaction (this occurs in molecules with two or more unpaired electrons, and is a magnetic-dipole / magnetic-dipole interaction)
- electron spin - molecular rotation (the rotation of a molecule corresponds to a magnetic dipole, which interacts with the magnetic dipole moment of the electron)
- electron spin - nuclear spin interaction (the interaction between the magnetic dipole moment of the electron and the magnetic dipole moment of the nuclei (if present)).
- electric field gradient - nuclear electric quadrupole interaction (the interaction between the electric field gradient of the electron cloud of the molecule and the electric quadrupole moments of nuclei (if present)).
- nuclear spin - nuclear spin interaction (nuclear magnetic moments interacting with one another).
These interactions give rise to the characteristic energy levels that are probed in "magnetic resonance" spectroscopy such as NMR
NMR spectroscopy
Nuclear magnetic resonance spectroscopy, most commonly known as NMR spectroscopy, is a research technique that exploits the magnetic properties of certain atomic nuclei to determine physical and chemical properties of atoms or the molecules in which they are contained...
and ESR, where they represent the "zero field splittings," which are always present.
Experimental determination of the spectrum
Fourier transform infrared (FTIR) spectroscopyFourier transform infrared spectroscopy
Fourier transform infrared spectroscopy is a technique which is used to obtain an infrared spectrum of absorption, emission, photoconductivity or Raman scattering of a solid, liquid or gas. An FTIR spectrometer simultaneously collects spectral data in a wide spectral range...
can be used to experimentally study rotational spectra. Typical spectra at these wavelengths involve rovibrational excitation, i.e., excitation of both a vibrational and a rotational mode of a molecule.
In the past, microwave spectra were determined using a simple arrangement in which low-pressure gas was introduced to a section of waveguide between a microwave source (of variable frequency) and a microwave detector. The spectrum was obtained by sweeping the frequency of the source while detecting the intensity of the transmitted radiation. This experimental arrangement has a major difficulty related to the propagation of microwave radiation through waveguides. The physical size of the waveguide restricts the frequency of the radiation that can be transmitted through it. For a given waveguide size (such as X-band), there is a cutoff frequency, and microwave radiation with smaller frequencies (longer wavelengths) cannot be propagated through the waveguide. In addition, as the frequency is increased, additional modes of propagation become possible, which correspond to different velocities of the radiation propagating down the waveguide (this can be envisaged as the radiation bouncing down the guide, at different angles of reflection). the net result of these considerations is that each size of waveguide is useful only over a rather narrow range of frequencies and must be physically swapped out for a different size of waveguide once this frequency range is exceeded.
From 1980 onward, microwave spectra have often been obtained using Fourier Transform Microwave Spectroscopy - a technique developed by W. H. Flygare at the University of Illinois.
Within the last two years, a further development of Fourier Transform Microwave Spectroscopy has occurred, which may well introduce a new renaissance into microwave spectroscopy. This is the use of "Chirped Pulses" to provide an electromagnetic wave that has as its Fourier Transform a very wide range of microwave frequencies. (see University of Virginia, Chemistry Department website).
Applications
Microwave spectroscopy is commonly used in physical chemistry to determine the structure of small molecules (such as ozone, methanol, or water) with high precision. Other common techniques for determining molecular structure, such as X-ray crystallographyX-ray crystallography
X-ray crystallography is a method of determining the arrangement of atoms within a crystal, in which a beam of X-rays strikes a crystal and causes the beam of light to spread into many specific directions. From the angles and intensities of these diffracted beams, a crystallographer can produce a...
do not work very well for some of these molecules (especially the gases) and are not as precise. However, microwave spectroscopy is not useful for determining the structures of large molecules such as proteins.
Modern microwave spectrometers have very high resolution. When hyperfine structure can be observed, the technique can also provide information on the electronic structures of molecules.
Microwave spectroscopy is one of the principal means by which the constituents of the universe are determined from the earth. It is particularly useful for detecting molecules in the interstellar medium (ISM)
Interstellar medium
In astronomy, the interstellar medium is the matter that exists in the space between the star systems in a galaxy. This matter includes gas in ionic, atomic, and molecular form, dust, and cosmic rays. It fills interstellar space and blends smoothly into the surrounding intergalactic space...
. One of the early surprises in interstellar chemistry came with the discovery of the existence in the ISM of long-chain carbon molecules. It was in attempting to research such molecules in the laboratory that Harry Kroto
Harold Kroto
Sir Harold Walter Kroto, FRS , born Harold Walter Krotoschiner, is a British chemist and one of the three recipients to share the 1996 Nobel Prize in Chemistry with Robert Curl and Richard Smalley....
was led to the laboratory of Rick Smalley
Richard Smalley
Richard Errett Smalley was the Gene and Norman Hackerman Professor of Chemistry and a Professor of Physics and Astronomy at Rice University, in Houston, Texas...
and Robert Curl
Robert Curl
Robert Floyd Curl, Jr. the son of a Methodist Minister is a graduate of Thomas Jefferson High School in San Antonio, Texas and is an emeritus professor of chemistry at Rice University....
, where it was possible to vaporize carbon under enormous energy conditions. This collaborative experiment led to the discovery of C60, buckminsterfullerene
Buckminsterfullerene
Buckminsterfullerene is a spherical fullerene molecule with the formula . It was first intentionally prepared in 1985 by Harold Kroto, James Heath, Sean O'Brien, Robert Curl and Richard Smalley at Rice University...
, which led to the award of the 1996 Nobel prize in chemistry to Kroto, Smalley and Curl.
See also
- SpectroscopySpectroscopySpectroscopy is the study of the interaction between matter and radiated energy. Historically, spectroscopy originated through the study of visible light dispersed according to its wavelength, e.g., by a prism. Later the concept was expanded greatly to comprise any interaction with radiative...
- Rigid rotorRigid rotorThe rigid rotor is a mechanical model that is used to explain rotating systems.An arbitrary rigid rotor is a 3-dimensional rigid object, such as a top. To orient such an object in space three angles are required. A special rigid rotor is the linear rotor which isa 2-dimensional object, requiring...
- Rovibronic excitation
- Vibrational spectroscopy
- Infrared spectroscopyInfrared spectroscopyInfrared spectroscopy is the spectroscopy that deals with the infrared region of the electromagnetic spectrum, that is light with a longer wavelength and lower frequency than visible light. It covers a range of techniques, mostly based on absorption spectroscopy. As with all spectroscopic...