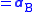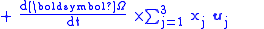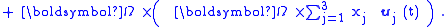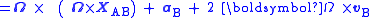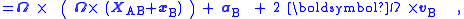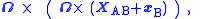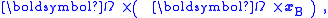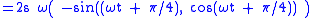
Fictitious force
Encyclopedia
A fictitious force, also called a pseudo force, d'Alembert force or inertial force, is an apparent force
that acts on all masses in a non-inertial frame of reference
, such as a rotating reference frame
.
The force F does not arise from any physical interaction
but rather from the acceleration a of the non-inertial reference frame
itself. As stated by Iro:
According to Newton's second law
in the form F = m a, fictitious forces always are proportional to the mass m acted upon.
A fictitious force arises when a frame of reference is accelerating compared to a non-accelerating frame. As a frame can accelerate in any arbitrary way, so can fictitious forces be as arbitrary (but only in direct response to the acceleration of the frame). However, four fictitious forces are defined for frames accelerated in commonly occurring ways: one caused by any relative acceleration of the origin in a straight line (rectilinear acceleration
), two caused by any rotation (centrifugal force
and Coriolis force) and a fourth, called the Euler force
, caused by a variable rate of rotation, should that occur.
. To solve classical mechanics
problems exactly in an Earth-bound reference frame, three fictitious forces must be introduced, the Coriolis force, the centrifugal force (described below) and the Euler force
. The Euler force is typically ignored because its magnitude is very small. Both of the other fictitious forces are weak compared to most typical forces in everyday life, but they can be detected under careful conditions. For example, Léon Foucault
was able to show the Coriolis force that results from the Earth's rotation using the Foucault pendulum
. If the Earth were to rotate a thousand times faster (making each day only ~86 seconds long), people could easily get the impression that such fictitious forces are pulling on them, as on a spinning carousel.
cannot detect their own motion; however, observers within an accelerating reference frame can detect that they are in a non-inertial reference frame from the fictitious forces that arise. For example, for straight-line acceleration:
Other accelerations also give rise to fictitious forces, as described mathematically below. The physical explanation of motions in an inertial frames is the simplest possible, requiring no fictitious forces: fictitious forces are zero, providing a means to distinguish inertial frames from others.
An example of the detection of a non-inertial, rotating reference frame is the precession of a Foucault pendulum
. In the non-inertial frame of the Earth, the fictitious Coriolis force is necessary to explain observations. In an inertial frame outside the Earth, no such fictitious force is necessary.
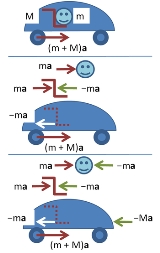
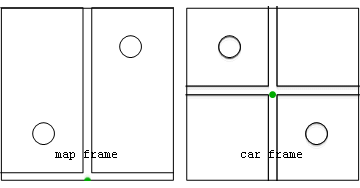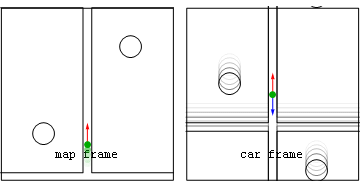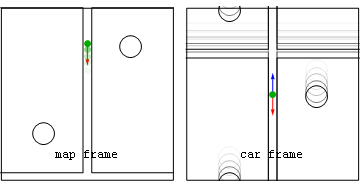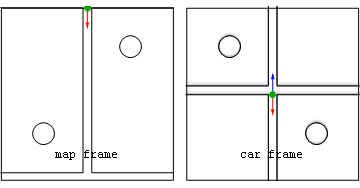
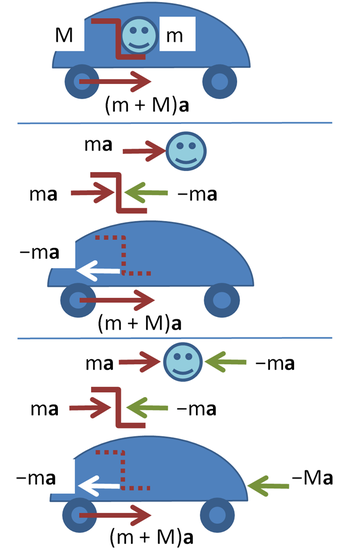Figure 1 (top) shows an accelerating car. When a car accelerates
, a passenger feels like they're being pushed back into the seat. In an inertial frame of reference attached to the road, there is no physical force moving the rider backward. However, in the rider's non-inertial reference frame attached to the accelerating car, there is a backward fictitious force. We mention two possible ways of analyzing the problem:
How can the accelerating frame be discovered to be non-inertial? In the accelerating frame, everything appears to be subject to zero net force, and nothing moves. Nonetheless, compression of the seat is observed and is explained in the accelerating frame (and in an inertial frame) by the force of acceleration on the seat from the car on one side, and the opposing force of reaction to acceleration by the passenger on the other. Identification of the accelerating frame as non-inertial cannot be based simply on the compression of the seat, which all observers can explain; rather it is based on the simplicity of the physical explanation for this compression.
The explanation of the seat compression in the accelerating frame requires not only the thrust from the axle of the car, but additional (fictitious) forces. In an inertial frame, only the thrust from the axle is necessary. Therefore, the inertial frame has a simpler physical explanation (not necessarily a simpler mathematical formulation, however), indicating the accelerating frame is a non-inertial frame of reference. In other words, in the inertial frame, fictitious forces are zero. See inertial frame for more detail.
This example illustrates how fictitious forces arise from switching from an inertial to a non-inertial reference frame. Calculations of physical quantities (compression of the seat, required force from the axle) made in any frame give the same answers, but in some cases calculations are easier to make in a non-inertial frame. (In this simple example, the calculations are equally complex for the two frames described.)
, circular from the standpoint of an inertial frame of reference attached to the road. When seen from a non-inertial frame of reference attached to the car, the fictitious force called the centrifugal force appears. If the car is moving at constant speed around a circular section of road, the occupants will feel pushed outside by this centrifugal force, away from the center of the turn. Again the situation can be viewed from inertial or non-inertial frames (for free body diagrams, see the turning car):
A classic example of fictitious force in circular motion is the experiment of rotating spheres tied by a cord and spinning around their center of mass. In this case, as with the linearly accelerating car example, the identification of a rotating, non-inertial frame of reference can be based upon the vanishing of fictitious forces. In an inertial frame, fictitious forces are not necessary to explain the tension in the string joining the spheres. In a rotating frame, Coriolis and centrifugal forces must be introduced to predict the observed tension.
To consider another example, where a rotating reference frame is very natural to us, namely the surface of the rotating Earth, centrifugal force reduces the apparent force of gravity by about one part in a thousand, depending on latitude. This reduction is zero at the poles, maximum at the equator.
The fictitious Coriolis force, which is observed in rotational frames, is ordinarily visible only in very large-scale motion like the projectile motion of long-range guns or the circulation of the Earth's atmosphere (see Rossby number
). Neglecting air resistance, an object dropped from a 50-meter-high tower at the equator
will fall 7.7 millimeters eastward of the spot below where it is dropped because of the Coriolis force.
In the case of distant objects and a rotating reference frame, what must be taken into account is the resultant force of centrifugal and Coriolis force. Consider a distant star observed from a rotating spacecraft. In the reference frame co-rotating with the spacecraft, the distant star appears to move along a circular trajectory around the spacecraft. The apparent motion of the star is an apparent centripetal acceleration. Just like in the example above of the car in circular motion, the centrifugal force has the same magnitude as the fictitious centripetal force, but is directed in the opposite, centrifugal direction. In this case the Coriolis force is twice the magnitude of the centrifugal force, and it points in centripetal direction. The vector sum of the centrifugal force and the Coriolis force is the total fictitious force, which in this case points in centripetal direction.
, provided that they move an object on a trajectory
that changes its energy
from potential
to kinetic
. For example, consider a person in a rotating chair holding a weight in his outstretched arm. If he pulls his arm inward, from the perspective of his rotating reference frame he has done work against centrifugal force. If he now lets go of the weight, from his perspective it spontaneously flies outward, because centrifugal force has done work on the object, converting its potential energy into kinetic. From an inertial viewpoint, of course, the object flies away from him because it is suddenly allowed to move in a straight line. This illustrates that the work done, like the total potential and kinetic energy of an object, can be different in a non-inertial frame than an inertial one.
to wonder whether gravity was a fictitious force as well. He noted that a freefalling observer in a closed box would not be able to detect the force of gravity; hence, freefalling reference frames are equivalent to an inertial reference frame (the equivalence principle
). Following up on this insight, Einstein was able to formulate a theory with gravity as a fictitious force; attributing the apparent acceleration of gravity to the curvature
of spacetime
. This idea underlies Einstein's theory of general relativity
. See Eötvös experiment
.
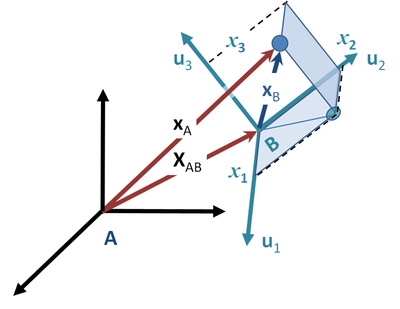
Figure 2 shows a particle with mass
m and position vector xA(t) in a particular inertial frame A. Consider a non-inertial frame B whose origin relative to the inertial one is given by XAB(t). Let the position of the particle in frame B be xB(t). What is the force on the particle as expressed in the coordinate system of frame B?
To answer this question, let the coordinate axis in B be represented by unit vectors uj with j any of { 1, 2, 3 } for the three coordinate axes. Then
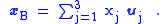
The interpretation of this equation is that xB is the vector displacement of the particle as expressed in terms of the coordinates in frame B at time t. From frame A the particle is located at:
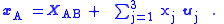
As an aside, the unit vectors { uj } cannot change magnitude, so derivatives of these vectors express only rotation of the coordinate system B. On the other hand, vector XAB simply locates the origin of frame B relative to frame A, and so cannot include rotation of frame B.
Taking a time derivative, the velocity of the particle is:
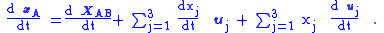
The second term summation is the velocity of the particle, say vB as measured in frame B. That is:
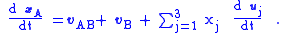
The interpretation of this equation is that the velocity of the particle seen by observers in frame A consists of what observers in frame B call the velocity, namely vB, plus two extra terms related to the rate of change of the frame-B coordinate axes. One of these is simply the velocity of the moving origin vAB. The other is a contribution to velocity due to the fact that different locations in the non-inertial frame have different apparent velocities due to rotation of the frame; a point seen from a rotating frame has a rotational component of velocity that is greater the further the point is from the origin.
To find the acceleration, another time differentiation provides:
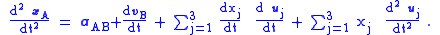
Using the same formula already used for the time derivative of xB, the velocity derivative on the right is:
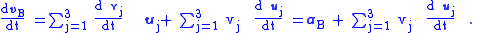
Consequently,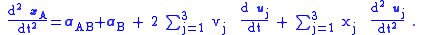
(Eq. 1)
The interpretation of this equation is as follows: the acceleration of the particle in frame A consists of what observers in frame B call the particle acceleration aB, but in addition there are three acceleration terms related to the movement of the frame-B coordinate axes: one term related to the acceleration of the origin of frame B, namely aAB, and two terms related to rotation of frame B. Consequently, observers in B will see the particle motion as possessing "extra" acceleration, which they will attribute to "forces" acting on the particle, but which observers in A say are "fictitious" forces arising simply because observers in B do not recognize the non-inertial nature of frame B.
The factor of two in the Coriolis force arises from two equal contributions: (i) the apparent change of an inertially constant velocity with time because rotation makes the direction of the velocity seem to change (a dvB / dt term) and (ii) an apparent change in the velocity of an object when its position changes, putting it nearer to or further from the axis of rotation (the change in Σxj uj due to change in x j ).
To put matters in terms of forces, the accelerations are multiplied by the particle mass:
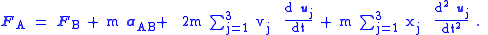
The force observed in frame B, FB = m aB is related to the actual force on the particle, FA, by:
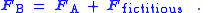
where:
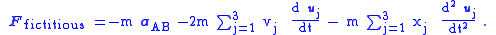
Thus, we can solve problems in frame B by assuming that Newton's second law holds (with respect to quantities in that frame) and treating Ffictitious as an additional force.
Below are a number of examples applying this result for fictitious forces. More examples can be found in the article on centrifugal force
.
To derive expressions for the fictitious forces, derivatives are needed for the apparent time rate of change of vectors that take into account time-variation of the coordinate axes. If the rotation of frame B is represented by a vector Ω pointed along the axis of rotation with orientation given by the right-hand rule
, and with magnitude given by
then the time derivative of any of the three unit vectors describing frame B is:
and
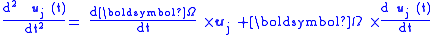
as is verified using the properties of the vector cross product. These derivative formulas now are applied to the relationship between acceleration in an inertial frame, and that in a coordinate frame rotating with time-varying angular velocity ω ( t ). From the previous section, where subscript A refers to the inertial frame and B to the rotating frame, setting aAB = 0 to remove any translational acceleration, and focusing on only rotational properties (see Eq. 1):
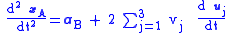
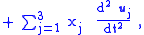
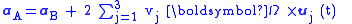
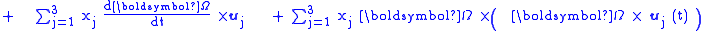
Collecting terms, the result is the so-called acceleration transformation formula:
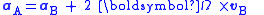
The physical acceleration
aA due to what observers in the inertial frame A call real external forces on the object is, therefore, not simply the acceleration aB seen by observers in the rotational frame B , but has several additional geometric acceleration terms associated with the rotation of B. As seen in the rotational frame, the acceleration aB of the particle is given by rearrangement of the above equation as: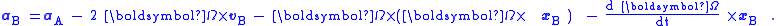
The net force upon the object according to observers in the rotating frame is FB = m aB. If their observations are to result in the correct force on the object when using Newton's laws, they must consider that the additional force Ffict is present, so the end result is FB = FA + Ffict. Thus, the fictitious force used by observers in B to get the correct behavior of the object from Newton's laws equals:
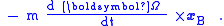
Here, the first term is the Coriolis force, the second term is the centrifugal force, and the third term is the Euler force
. When the rate of rotation doesn't change, as is typically the case for a planet, the Euler force is zero.
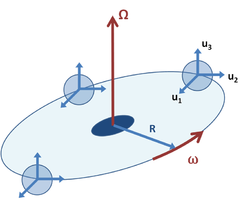As a related example, suppose the moving coordinate system B rotates in a circle of radius R about the fixed origin of inertial frame A, but maintains its coordinate axes fixed in orientation, as in Figure 3. The acceleration of an observed body is now (see Eq. 1):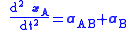
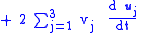
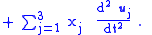
where the summations are zero inasmuch as the unit vectors have no time dependence. The origin of system B is located according to frame A at: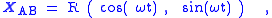
leading to a velocity of the origin of frame B as:
leading to an acceleration of the origin of B given by: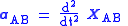
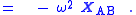
Because the first term, which is
is of the same form as the normal centrifugal force expression:
it is a natural extension of standard terminology (although there is no standard terminology for this case) to call this term a "centrifugal force". Whatever terminology is adopted, the observers in frame B must introduce a fictitious force, this time due to the acceleration from the orbital motion of their entire coordinate frame, that is radially outward away from the center of rotation of the origin of their coordinate system: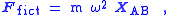
and of magnitude:
Notice that this "centrifugal force" has differences from the case of a rotating frame. In the rotating frame the centrifugal force is related to the distance of the object from the origin of frame B, while in the case of an orbiting frame, the centrifugal force is independent of the distance of the object from the origin of frame B, but instead depends upon the distance of the origin of frame B from its center of rotation, resulting in the same centrifugal fictitious force for all objects observed in frame B.
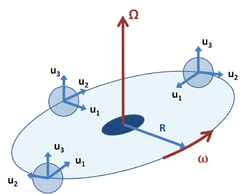As a combination example, Figure 4 shows a coordinate system B that orbits inertial frame A as in Figure 3, but the coordinate axes in frame B turn so unit vector u1 always points toward the center of rotation. This example might apply to a test tube in a centrifuge, where vector u1 points along the axis of the tube toward its opening at its top. It also resembles the Earth-Moon system, where the Moon always presents the same face to the Earth. In this example, unit vector u3 retains a fixed orientation, while vectors u1, u2 rotate at the same rate as the origin of coordinates. That is,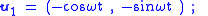
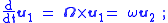
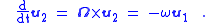
Hence, the acceleration of a moving object is expressed as (see Eq. 1):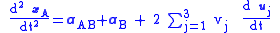
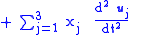
where the angular acceleration term is zero for constant rate of rotation.
Because the first term, which is
is of the same form as the normal centrifugal force expression:
it is a natural extension of standard terminology (although there is no standard terminology for this case) to call this term the "centrifugal force". Applying this terminology to the example of a tube in a centrifuge, if the tube is far enough from the center of rotation, |XAB| = R >> |xB|, all the matter in the test tube sees the same acceleration (the same centrifugal force). Thus, in this case, the fictitious force is primarily a uniform centrifugal force along the axis of the tube, away from the center of rotation, with a value |FFict| = ω2 R, where R is the distance of the matter in the tube from the center of the centrifuge. It is standard specification of a centrifuge to use the "effective" radius of the centrifuge to estimate its ability to provided centrifugal force. Thus, a first estimate of centrifugal force in a centrifuge can be based upon the distance of the tubes from the center of rotation, and corrections applied if needed.
Also, the test tube confines motion to the direction down the length of the tube, so vB is opposite to u1 and the Coriolis force is opposite to u2, that is, against the wall of the tube. If the tube is spun for a long enough time, the velocity vB drops to zero as the matter comes to an equilibrium distribution. For more details, see the articles on sedimentation
and the Lamm equation
.
A related problem is that of centrifugal forces for the Earth-Moon-Sun system, where three rotations appear: the daily rotation of the Earth about its axis, the lunar-month rotation of the Earth-Moon system about their center of mass, and the annual revolution of the Earth-Moon system about the Sun. These three motions influence the tides.
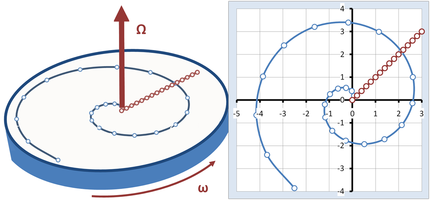Figure 5 shows another example comparing the observations of an inertial observer with those of an observer on a rotating carousel
. The carousel rotates at a constant angular velocity represented by the vector Ω with magnitude ω, pointing upward according to the right-hand rule
. A rider on the carousel walks radially across it at constant speed, in what appears to the walker to be the straight line path inclined at 45° in Figure 5 . To the stationary observer, however, the walker travels a spiral path. The points identified on both paths in Figure 5 correspond to the same times spaced at equal time intervals. We ask how two observers, one on the carousel and one in an inertial frame, formulate what they see using Newton's laws.
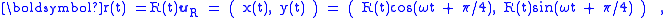
where the added π/4 sets the path angle at 45° to start with (just an arbitrary choice of direction), uR is a unit vector in the radial direction pointing from the center of the carousel to the walker at time t. The radial distance R(t) increases steadily with time according to:
with s the speed of walking. According to simple kinematics, the velocity is then the first derivative of the trajectory: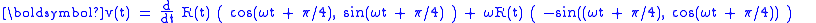
with uθ a unit vector perpendicular to uR at time t (as can be verified by noticing that the vector dot product
with the radial vector is zero) and pointing in the direction of travel.
The acceleration is the first derivative of the velocity: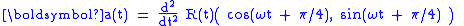
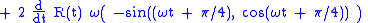
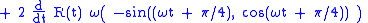
The last term in the acceleration is radially inward of magnitude ω2 R, which is therefore the instantaneous centripetal acceleration
of circular motion
. The first term is perpendicular to the radial direction, and pointing in the direction of travel. Its magnitude is 2sω, and it represents the acceleration of the walker as the edge of the carousel is neared, and the arc of circle traveled in a fixed time increases, as can be seen by the increased spacing between points for equal time steps on the spiral in Figure 5 as the outer edge of the carousel is approached.
Applying Newton's laws, multiplying the acceleration by the mass of the walker, the inertial observer concludes that the walker is subject to two forces: the inward, radially directed centripetal force, and another force perpendicular to the radial direction that is proportional to the speed of the walker.
To agree with the inertial observer, the forces applied to the walker must be exactly those found above. They can be related to the general formulas already derived, namely:
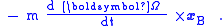
In this example, the velocity seen in the rotating frame is:
with uR a unit vector in the radial direction. The position of the walker as seen on the carousel is: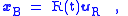
and the time derivative of Ω is zero for uniform angular rotation. Noticing that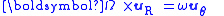
and
we find: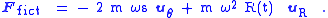
To obtain a straight-line motion in the rotating world, a force exactly opposite in sign to the fictitious force must be applied to reduce the net force on the walker to zero, so Newton's law of inertia will predict a straight line motion, in agreement with what the rotating observer sees. The fictitious forces that must be combated are the Coriolis force (first term) and the centrifugal force
(second term). (These terms are approximate.) By applying forces to counter these two fictitious forces, the rotating observer ends up applying exactly the same forces upon the walker that the inertial observer predicted were needed.
Because they differ only by the constant walking velocity, the walker and the rotational observer see the same accelerations. From the walker's perspective, the fictitious force is experienced as real, and combating this force is necessary to stay on a straight line radial path holding constant speed. It's like battling a crosswind while being thrown to the edge of the carousel.
discussion does not delve into the mechanism by which the required forces are generated. That is the subject of kinetics
. In the case of the carousel, the kinetic discussion would involve perhaps a study of the walker's shoes and the friction they need to generate against the floor of the carousel, or perhaps the dynamics of skateboarding, if the walker switched to travel by skateboard. Whatever the means of travel across the carousel, the forces calculated above must be realized. A very rough analogy is heating your house: you must have a certain temperature to be comfortable, but whether you heat by burning gas or by burning coal is another problem. Kinematics sets the thermostat, kinetics fires the furnace.
Force
In physics, a force is any influence that causes an object to undergo a change in speed, a change in direction, or a change in shape. In other words, a force is that which can cause an object with mass to change its velocity , i.e., to accelerate, or which can cause a flexible object to deform...
that acts on all masses in a non-inertial frame of reference
Non-inertial reference frame
A non-inertial reference frame is a frame of reference that is under acceleration. The laws of physics in such a frame do not take on their most simple form, as required by the theory of special relativity...
, such as a rotating reference frame
Rotating reference frame
A rotating frame of reference is a special case of a non-inertial reference frame that is rotating relative to an inertial reference frame. An everyday example of a rotating reference frame is the surface of the Earth. A rotating frame of reference is a special case of a non-inertial reference...
.
The force F does not arise from any physical interaction
Force carrier
In particle physics, quantum field theories such as the Standard Model describe nature in terms of fields. Each field has a complementary description as the set of particles of a particular type...
but rather from the acceleration a of the non-inertial reference frame
Non-inertial reference frame
A non-inertial reference frame is a frame of reference that is under acceleration. The laws of physics in such a frame do not take on their most simple form, as required by the theory of special relativity...
itself. As stated by Iro:
According to Newton's second law
Newton's laws of motion
Newton's laws of motion are three physical laws that form the basis for classical mechanics. They describe the relationship between the forces acting on a body and its motion due to those forces...
in the form F = m a, fictitious forces always are proportional to the mass m acted upon.
A fictitious force arises when a frame of reference is accelerating compared to a non-accelerating frame. As a frame can accelerate in any arbitrary way, so can fictitious forces be as arbitrary (but only in direct response to the acceleration of the frame). However, four fictitious forces are defined for frames accelerated in commonly occurring ways: one caused by any relative acceleration of the origin in a straight line (rectilinear acceleration
Acceleration
In physics, acceleration is the rate of change of velocity with time. In one dimension, acceleration is the rate at which something speeds up or slows down. However, since velocity is a vector, acceleration describes the rate of change of both the magnitude and the direction of velocity. ...
), two caused by any rotation (centrifugal force
Centrifugal force
Centrifugal force can generally be any force directed outward relative to some origin. More particularly, in classical mechanics, the centrifugal force is an outward force which arises when describing the motion of objects in a rotating reference frame...
and Coriolis force) and a fourth, called the Euler force
Euler force
In classical mechanics, the Euler acceleration , also known as azimuthal acceleration or transverse acceleration is an acceleration that appears when a non-uniformly rotating reference frame is used for analysis of motion and there is variation in the angular velocity of the reference frame's axes...
, caused by a variable rate of rotation, should that occur.
Background
The role of fictitious forces in Newtonian mechanics is described by Tonnelat:Fictitious forces on Earth
The surface of the Earth is a rotating reference frameRotating reference frame
A rotating frame of reference is a special case of a non-inertial reference frame that is rotating relative to an inertial reference frame. An everyday example of a rotating reference frame is the surface of the Earth. A rotating frame of reference is a special case of a non-inertial reference...
. To solve classical mechanics
Classical mechanics
In physics, classical mechanics is one of the two major sub-fields of mechanics, which is concerned with the set of physical laws describing the motion of bodies under the action of a system of forces...
problems exactly in an Earth-bound reference frame, three fictitious forces must be introduced, the Coriolis force, the centrifugal force (described below) and the Euler force
Euler force
In classical mechanics, the Euler acceleration , also known as azimuthal acceleration or transverse acceleration is an acceleration that appears when a non-uniformly rotating reference frame is used for analysis of motion and there is variation in the angular velocity of the reference frame's axes...
. The Euler force is typically ignored because its magnitude is very small. Both of the other fictitious forces are weak compared to most typical forces in everyday life, but they can be detected under careful conditions. For example, Léon Foucault
Léon Foucault
Jean Bernard Léon Foucault was a French physicist best known for the invention of the Foucault pendulum, a device demonstrating the effect of the Earth's rotation...
was able to show the Coriolis force that results from the Earth's rotation using the Foucault pendulum
Foucault pendulum
The Foucault pendulum , or Foucault's pendulum, named after the French physicist Léon Foucault, is a simple device conceived as an experiment to demonstrate the rotation of the Earth. While it had long been known that the Earth rotated, the introduction of the Foucault pendulum in 1851 was the...
. If the Earth were to rotate a thousand times faster (making each day only ~86 seconds long), people could easily get the impression that such fictitious forces are pulling on them, as on a spinning carousel.
Detection of non-inertial reference frame
Observers inside a closed box that is moving with a constant velocityVelocity
In physics, velocity is speed in a given direction. Speed describes only how fast an object is moving, whereas velocity gives both the speed and direction of the object's motion. To have a constant velocity, an object must have a constant speed and motion in a constant direction. Constant ...
cannot detect their own motion; however, observers within an accelerating reference frame can detect that they are in a non-inertial reference frame from the fictitious forces that arise. For example, for straight-line acceleration:
Other accelerations also give rise to fictitious forces, as described mathematically below. The physical explanation of motions in an inertial frames is the simplest possible, requiring no fictitious forces: fictitious forces are zero, providing a means to distinguish inertial frames from others.
An example of the detection of a non-inertial, rotating reference frame is the precession of a Foucault pendulum
Foucault pendulum
The Foucault pendulum , or Foucault's pendulum, named after the French physicist Léon Foucault, is a simple device conceived as an experiment to demonstrate the rotation of the Earth. While it had long been known that the Earth rotated, the introduction of the Foucault pendulum in 1851 was the...
. In the non-inertial frame of the Earth, the fictitious Coriolis force is necessary to explain observations. In an inertial frame outside the Earth, no such fictitious force is necessary.
Acceleration in a straight line
Acceleration
In physics, acceleration is the rate of change of velocity with time. In one dimension, acceleration is the rate at which something speeds up or slows down. However, since velocity is a vector, acceleration describes the rate of change of both the magnitude and the direction of velocity. ...
, a passenger feels like they're being pushed back into the seat. In an inertial frame of reference attached to the road, there is no physical force moving the rider backward. However, in the rider's non-inertial reference frame attached to the accelerating car, there is a backward fictitious force. We mention two possible ways of analyzing the problem:
- Figure 1, (center panel). From an inertial reference frame, with a constant velocity matching the initial motion of the car, the car is accelerating. In order for the passenger to stay inside the car, a force must be exerted on them. This force is exerted by the seat, which has started to move forward with the car and is compressed against the passenger until it transmits the full force to keep the passenger moving with the car. Thus, the forces of the seat are unbalanced, so the passenger is accelerating in this frame.
- Figure 1, (bottom panel). From the point of view of the interior of the car, an accelerating reference frame, there is a fictitious force pushing the passenger backwards, with magnitude equal to the massMassMass can be defined as a quantitive measure of the resistance an object has to change in its velocity.In physics, mass commonly refers to any of the following three properties of matter, which have been shown experimentally to be equivalent:...
of the passenger times the acceleration of the car. This force pushes the passenger back into the seat, until the seat compresses and provides an equal and opposite force. Thereafter, the passenger is stationary in this frame, because the fictitious force and the real force of the seat are balanced.
How can the accelerating frame be discovered to be non-inertial? In the accelerating frame, everything appears to be subject to zero net force, and nothing moves. Nonetheless, compression of the seat is observed and is explained in the accelerating frame (and in an inertial frame) by the force of acceleration on the seat from the car on one side, and the opposing force of reaction to acceleration by the passenger on the other. Identification of the accelerating frame as non-inertial cannot be based simply on the compression of the seat, which all observers can explain; rather it is based on the simplicity of the physical explanation for this compression.
The explanation of the seat compression in the accelerating frame requires not only the thrust from the axle of the car, but additional (fictitious) forces. In an inertial frame, only the thrust from the axle is necessary. Therefore, the inertial frame has a simpler physical explanation (not necessarily a simpler mathematical formulation, however), indicating the accelerating frame is a non-inertial frame of reference. In other words, in the inertial frame, fictitious forces are zero. See inertial frame for more detail.
This example illustrates how fictitious forces arise from switching from an inertial to a non-inertial reference frame. Calculations of physical quantities (compression of the seat, required force from the axle) made in any frame give the same answers, but in some cases calculations are easier to make in a non-inertial frame. (In this simple example, the calculations are equally complex for the two frames described.)
| Animation: driving from block to block |
|---|
 |
Circular motion
A similar effect occurs in circular motionCircular motion
In physics, circular motion is rotation along a circular path or a circular orbit. It can be uniform, that is, with constant angular rate of rotation , or non-uniform, that is, with a changing rate of rotation. The rotation around a fixed axis of a three-dimensional body involves circular motion of...
, circular from the standpoint of an inertial frame of reference attached to the road. When seen from a non-inertial frame of reference attached to the car, the fictitious force called the centrifugal force appears. If the car is moving at constant speed around a circular section of road, the occupants will feel pushed outside by this centrifugal force, away from the center of the turn. Again the situation can be viewed from inertial or non-inertial frames (for free body diagrams, see the turning car):
- From the viewpoint of an inertial reference frame stationary with respect to the road, the car is accelerating toward the center of the circle. This acceleration is necessary because the direction of the velocity is changing, despite a constant speed. This inward acceleration is called centripetal acceleration and requires a centripetal forceCentripetal forceCentripetal force is a force that makes a body follow a curved path: it is always directed orthogonal to the velocity of the body, toward the instantaneous center of curvature of the path. The mathematical description was derived in 1659 by Dutch physicist Christiaan Huygens...
to maintain the circular motion. This force is exerted by the ground upon the wheels, in this case thanks to the frictionFrictionFriction is the force resisting the relative motion of solid surfaces, fluid layers, and/or material elements sliding against each other. There are several types of friction:...
between the wheels and the road. The car is accelerating, due to the unbalanced force, which causes it to move in a circle. (See also banked turn.) - From the viewpoint of a rotating frame, moving with the car, there is a fictitious centrifugal force that tends to push the car toward the outside of the road (and to push the occupants toward the outside of the car). The centrifugal force balances the friction between wheels and road, making the car stationary in this non-inertial frame.
A classic example of fictitious force in circular motion is the experiment of rotating spheres tied by a cord and spinning around their center of mass. In this case, as with the linearly accelerating car example, the identification of a rotating, non-inertial frame of reference can be based upon the vanishing of fictitious forces. In an inertial frame, fictitious forces are not necessary to explain the tension in the string joining the spheres. In a rotating frame, Coriolis and centrifugal forces must be introduced to predict the observed tension.
To consider another example, where a rotating reference frame is very natural to us, namely the surface of the rotating Earth, centrifugal force reduces the apparent force of gravity by about one part in a thousand, depending on latitude. This reduction is zero at the poles, maximum at the equator.
| Animation: object released from a carousel |
|---|
 |
The fictitious Coriolis force, which is observed in rotational frames, is ordinarily visible only in very large-scale motion like the projectile motion of long-range guns or the circulation of the Earth's atmosphere (see Rossby number
Rossby number
The Rossby number, named for Carl-Gustav Arvid Rossby, is a dimensionless number used in describing fluid flow. The Rossby number is the ratio of inertial to Coriolis force, terms v\cdot\nabla v\sim U^2 / L and \Omega\times v\sim U\Omega in the Navier–Stokes equations, respectively...
). Neglecting air resistance, an object dropped from a 50-meter-high tower at the equator
Equator
An equator is the intersection of a sphere's surface with the plane perpendicular to the sphere's axis of rotation and containing the sphere's center of mass....
will fall 7.7 millimeters eastward of the spot below where it is dropped because of the Coriolis force.
In the case of distant objects and a rotating reference frame, what must be taken into account is the resultant force of centrifugal and Coriolis force. Consider a distant star observed from a rotating spacecraft. In the reference frame co-rotating with the spacecraft, the distant star appears to move along a circular trajectory around the spacecraft. The apparent motion of the star is an apparent centripetal acceleration. Just like in the example above of the car in circular motion, the centrifugal force has the same magnitude as the fictitious centripetal force, but is directed in the opposite, centrifugal direction. In this case the Coriolis force is twice the magnitude of the centrifugal force, and it points in centripetal direction. The vector sum of the centrifugal force and the Coriolis force is the total fictitious force, which in this case points in centripetal direction.
Fictitious forces and work
Fictitious forces can be considered to do workMechanical work
In physics, work is a scalar quantity that can be described as the product of a force times the distance through which it acts, and it is called the work of the force. Only the component of a force in the direction of the movement of its point of application does work...
, provided that they move an object on a trajectory
Trajectory
A trajectory is the path that a moving object follows through space as a function of time. The object might be a projectile or a satellite, for example. It thus includes the meaning of orbit—the path of a planet, an asteroid or a comet as it travels around a central mass...
that changes its energy
Energy
In physics, energy is an indirectly observed quantity. It is often understood as the ability a physical system has to do work on other physical systems...
from potential
Potential energy
In physics, potential energy is the energy stored in a body or in a system due to its position in a force field or due to its configuration. The SI unit of measure for energy and work is the Joule...
to kinetic
Kinetic energy
The kinetic energy of an object is the energy which it possesses due to its motion.It is defined as the work needed to accelerate a body of a given mass from rest to its stated velocity. Having gained this energy during its acceleration, the body maintains this kinetic energy unless its speed changes...
. For example, consider a person in a rotating chair holding a weight in his outstretched arm. If he pulls his arm inward, from the perspective of his rotating reference frame he has done work against centrifugal force. If he now lets go of the weight, from his perspective it spontaneously flies outward, because centrifugal force has done work on the object, converting its potential energy into kinetic. From an inertial viewpoint, of course, the object flies away from him because it is suddenly allowed to move in a straight line. This illustrates that the work done, like the total potential and kinetic energy of an object, can be different in a non-inertial frame than an inertial one.
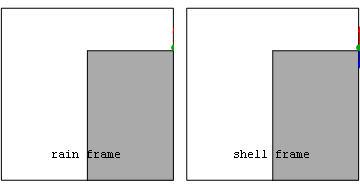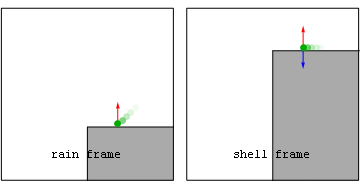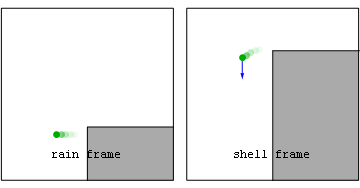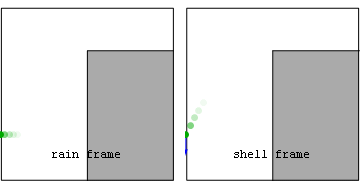
Gravity as a fictitious force
The notion of "fictitious force" comes up in general relativity. All fictitious forces are proportional to the mass of the object upon which they act, which is also true for gravity. This led Albert EinsteinAlbert Einstein
Albert Einstein was a German-born theoretical physicist who developed the theory of general relativity, effecting a revolution in physics. For this achievement, Einstein is often regarded as the father of modern physics and one of the most prolific intellects in human history...
to wonder whether gravity was a fictitious force as well. He noted that a freefalling observer in a closed box would not be able to detect the force of gravity; hence, freefalling reference frames are equivalent to an inertial reference frame (the equivalence principle
Equivalence principle
In the physics of general relativity, the equivalence principle is any of several related concepts dealing with the equivalence of gravitational and inertial mass, and to Albert Einstein's assertion that the gravitational "force" as experienced locally while standing on a massive body is actually...
). Following up on this insight, Einstein was able to formulate a theory with gravity as a fictitious force; attributing the apparent acceleration of gravity to the curvature
Curvature
In mathematics, curvature refers to any of a number of loosely related concepts in different areas of geometry. Intuitively, curvature is the amount by which a geometric object deviates from being flat, or straight in the case of a line, but this is defined in different ways depending on the context...
of spacetime
Spacetime
In physics, spacetime is any mathematical model that combines space and time into a single continuum. Spacetime is usually interpreted with space as being three-dimensional and time playing the role of a fourth dimension that is of a different sort from the spatial dimensions...
. This idea underlies Einstein's theory of general relativity
General relativity
General relativity or the general theory of relativity is the geometric theory of gravitation published by Albert Einstein in 1916. It is the current description of gravitation in modern physics...
. See Eötvös experiment
Eötvös experiment
The Eötvös experiment was a famous physics experiment that measured the correlation between inertial mass and gravitational mass, demonstrating that the two were one and the same, something that had long been suspected but never demonstrated with the same accuracy. The earliest experiments were...
.
| Animation: ball that rolls off a cliff |
|---|
 |
Mathematical derivation of fictitious forces
General derivation
Many problems require use of noninertial reference frames, for example, those involving satellites and particle accelerators.Figure 2 shows a particle with mass
Mass
Mass can be defined as a quantitive measure of the resistance an object has to change in its velocity.In physics, mass commonly refers to any of the following three properties of matter, which have been shown experimentally to be equivalent:...
m and position vector xA(t) in a particular inertial frame A. Consider a non-inertial frame B whose origin relative to the inertial one is given by XAB(t). Let the position of the particle in frame B be xB(t). What is the force on the particle as expressed in the coordinate system of frame B?
To answer this question, let the coordinate axis in B be represented by unit vectors uj with j any of { 1, 2, 3 } for the three coordinate axes. Then
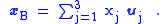
The interpretation of this equation is that xB is the vector displacement of the particle as expressed in terms of the coordinates in frame B at time t. From frame A the particle is located at:
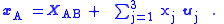
As an aside, the unit vectors { uj } cannot change magnitude, so derivatives of these vectors express only rotation of the coordinate system B. On the other hand, vector XAB simply locates the origin of frame B relative to frame A, and so cannot include rotation of frame B.
Taking a time derivative, the velocity of the particle is:
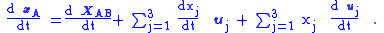
The second term summation is the velocity of the particle, say vB as measured in frame B. That is:
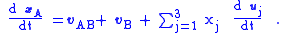
The interpretation of this equation is that the velocity of the particle seen by observers in frame A consists of what observers in frame B call the velocity, namely vB, plus two extra terms related to the rate of change of the frame-B coordinate axes. One of these is simply the velocity of the moving origin vAB. The other is a contribution to velocity due to the fact that different locations in the non-inertial frame have different apparent velocities due to rotation of the frame; a point seen from a rotating frame has a rotational component of velocity that is greater the further the point is from the origin.
To find the acceleration, another time differentiation provides:
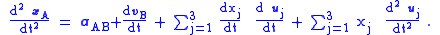
Using the same formula already used for the time derivative of xB, the velocity derivative on the right is:
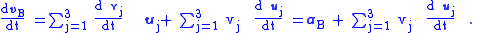
Consequently,
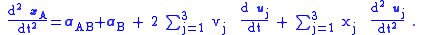(Eq. 1)The interpretation of this equation is as follows: the acceleration of the particle in frame A consists of what observers in frame B call the particle acceleration aB, but in addition there are three acceleration terms related to the movement of the frame-B coordinate axes: one term related to the acceleration of the origin of frame B, namely aAB, and two terms related to rotation of frame B. Consequently, observers in B will see the particle motion as possessing "extra" acceleration, which they will attribute to "forces" acting on the particle, but which observers in A say are "fictitious" forces arising simply because observers in B do not recognize the non-inertial nature of frame B.
The factor of two in the Coriolis force arises from two equal contributions: (i) the apparent change of an inertially constant velocity with time because rotation makes the direction of the velocity seem to change (a dvB / dt term) and (ii) an apparent change in the velocity of an object when its position changes, putting it nearer to or further from the axis of rotation (the change in Σxj uj due to change in x j ).
To put matters in terms of forces, the accelerations are multiplied by the particle mass:
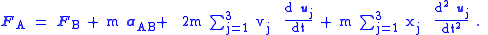
The force observed in frame B, FB = m aB is related to the actual force on the particle, FA, by:
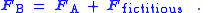
where:
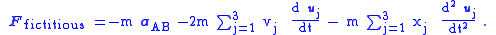
Thus, we can solve problems in frame B by assuming that Newton's second law holds (with respect to quantities in that frame) and treating Ffictitious as an additional force.
Below are a number of examples applying this result for fictitious forces. More examples can be found in the article on centrifugal force
Centrifugal force
Centrifugal force can generally be any force directed outward relative to some origin. More particularly, in classical mechanics, the centrifugal force is an outward force which arises when describing the motion of objects in a rotating reference frame...
.
Rotating coordinate systems
A common situation in which noninertial reference frames are useful is when the reference frame is rotating. Because such rotational motion is non-inertial, due to the acceleration present in any rotational motion, a fictitious force can always be invoked by using a rotational frame of reference. Despite this complication, the use of fictitious forces often simplifies the calculations involved.To derive expressions for the fictitious forces, derivatives are needed for the apparent time rate of change of vectors that take into account time-variation of the coordinate axes. If the rotation of frame B is represented by a vector Ω pointed along the axis of rotation with orientation given by the right-hand rule
Right-hand rule
In mathematics and physics, the right-hand rule is a common mnemonic for understanding notation conventions for vectors in 3 dimensions. It was invented for use in electromagnetism by British physicist John Ambrose Fleming in the late 19th century....
, and with magnitude given by
then the time derivative of any of the three unit vectors describing frame B is:
and
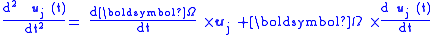
as is verified using the properties of the vector cross product. These derivative formulas now are applied to the relationship between acceleration in an inertial frame, and that in a coordinate frame rotating with time-varying angular velocity ω ( t ). From the previous section, where subscript A refers to the inertial frame and B to the rotating frame, setting aAB = 0 to remove any translational acceleration, and focusing on only rotational properties (see Eq. 1):
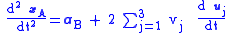
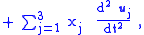
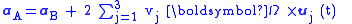
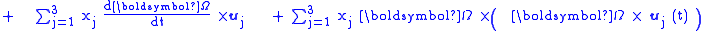
Collecting terms, the result is the so-called acceleration transformation formula:
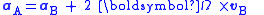
The physical acceleration
Proper acceleration
In relativity theory, proper acceleration is the physical acceleration experienced by an object. It is acceleration relative to a free-fall, or inertial, observer who is momentarily at rest relative to the object being measured...
aA due to what observers in the inertial frame A call real external forces on the object is, therefore, not simply the acceleration aB seen by observers in the rotational frame B , but has several additional geometric acceleration terms associated with the rotation of B. As seen in the rotational frame, the acceleration aB of the particle is given by rearrangement of the above equation as:
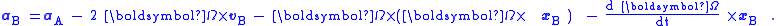
The net force upon the object according to observers in the rotating frame is FB = m aB. If their observations are to result in the correct force on the object when using Newton's laws, they must consider that the additional force Ffict is present, so the end result is FB = FA + Ffict. Thus, the fictitious force used by observers in B to get the correct behavior of the object from Newton's laws equals:
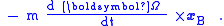
Here, the first term is the Coriolis force, the second term is the centrifugal force, and the third term is the Euler force
Euler force
In classical mechanics, the Euler acceleration , also known as azimuthal acceleration or transverse acceleration is an acceleration that appears when a non-uniformly rotating reference frame is used for analysis of motion and there is variation in the angular velocity of the reference frame's axes...
. When the rate of rotation doesn't change, as is typically the case for a planet, the Euler force is zero.
Orbiting coordinate systems
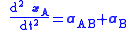
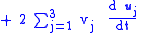
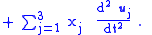
where the summations are zero inasmuch as the unit vectors have no time dependence. The origin of system B is located according to frame A at:
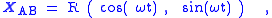
leading to a velocity of the origin of frame B as:
leading to an acceleration of the origin of B given by:
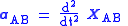
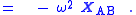
Because the first term, which is
is of the same form as the normal centrifugal force expression:
it is a natural extension of standard terminology (although there is no standard terminology for this case) to call this term a "centrifugal force". Whatever terminology is adopted, the observers in frame B must introduce a fictitious force, this time due to the acceleration from the orbital motion of their entire coordinate frame, that is radially outward away from the center of rotation of the origin of their coordinate system:
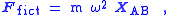
and of magnitude:
Notice that this "centrifugal force" has differences from the case of a rotating frame. In the rotating frame the centrifugal force is related to the distance of the object from the origin of frame B, while in the case of an orbiting frame, the centrifugal force is independent of the distance of the object from the origin of frame B, but instead depends upon the distance of the origin of frame B from its center of rotation, resulting in the same centrifugal fictitious force for all objects observed in frame B.
Orbiting and rotating
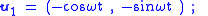
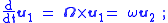
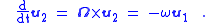
Hence, the acceleration of a moving object is expressed as (see Eq. 1):
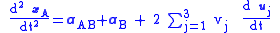
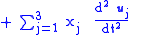
where the angular acceleration term is zero for constant rate of rotation.
Because the first term, which is
is of the same form as the normal centrifugal force expression:
it is a natural extension of standard terminology (although there is no standard terminology for this case) to call this term the "centrifugal force". Applying this terminology to the example of a tube in a centrifuge, if the tube is far enough from the center of rotation, |XAB| = R >> |xB|, all the matter in the test tube sees the same acceleration (the same centrifugal force). Thus, in this case, the fictitious force is primarily a uniform centrifugal force along the axis of the tube, away from the center of rotation, with a value |FFict| = ω2 R, where R is the distance of the matter in the tube from the center of the centrifuge. It is standard specification of a centrifuge to use the "effective" radius of the centrifuge to estimate its ability to provided centrifugal force. Thus, a first estimate of centrifugal force in a centrifuge can be based upon the distance of the tubes from the center of rotation, and corrections applied if needed.
Also, the test tube confines motion to the direction down the length of the tube, so vB is opposite to u1 and the Coriolis force is opposite to u2, that is, against the wall of the tube. If the tube is spun for a long enough time, the velocity vB drops to zero as the matter comes to an equilibrium distribution. For more details, see the articles on sedimentation
Sedimentation
Sedimentation is the tendency for particles in suspension to settle out of the fluid in which they are entrained, and come to rest against a barrier. This is due to their motion through the fluid in response to the forces acting on them: these forces can be due to gravity, centrifugal acceleration...
and the Lamm equation
Lamm equation
The Lamm equation describes the sedimentation and diffusion of a solute under ultracentrifugation in traditional sector-shaped cells. It was named after Ole Lamm, later professor of physical chemistry at the Royal Institute of Technology, who derived it during his Ph.D...
.
A related problem is that of centrifugal forces for the Earth-Moon-Sun system, where three rotations appear: the daily rotation of the Earth about its axis, the lunar-month rotation of the Earth-Moon system about their center of mass, and the annual revolution of the Earth-Moon system about the Sun. These three motions influence the tides.
Crossing a carousel
Carousel
A carousel , or merry-go-round, is an amusement ride consisting of a rotating circular platform with seats for riders...
. The carousel rotates at a constant angular velocity represented by the vector Ω with magnitude ω, pointing upward according to the right-hand rule
Right-hand rule
In mathematics and physics, the right-hand rule is a common mnemonic for understanding notation conventions for vectors in 3 dimensions. It was invented for use in electromagnetism by British physicist John Ambrose Fleming in the late 19th century....
. A rider on the carousel walks radially across it at constant speed, in what appears to the walker to be the straight line path inclined at 45° in Figure 5 . To the stationary observer, however, the walker travels a spiral path. The points identified on both paths in Figure 5 correspond to the same times spaced at equal time intervals. We ask how two observers, one on the carousel and one in an inertial frame, formulate what they see using Newton's laws.
Inertial observer
The observer at rest describes the path followed by the walker as a spiral. Adopting the coordinate system shown in Figure 5, the trajectory is described by r ( t ):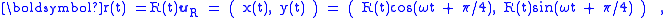where the added π/4 sets the path angle at 45° to start with (just an arbitrary choice of direction), uR is a unit vector in the radial direction pointing from the center of the carousel to the walker at time t. The radial distance R(t) increases steadily with time according to:
with s the speed of walking. According to simple kinematics, the velocity is then the first derivative of the trajectory:
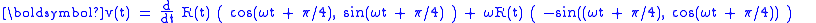
with uθ a unit vector perpendicular to uR at time t (as can be verified by noticing that the vector dot product
Dot product
In mathematics, the dot product or scalar product is an algebraic operation that takes two equal-length sequences of numbers and returns a single number obtained by multiplying corresponding entries and then summing those products...
with the radial vector is zero) and pointing in the direction of travel.
The acceleration is the first derivative of the velocity:
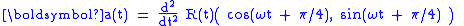
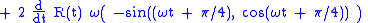
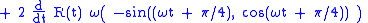
The last term in the acceleration is radially inward of magnitude ω2 R, which is therefore the instantaneous centripetal acceleration
Centripetal force
Centripetal force is a force that makes a body follow a curved path: it is always directed orthogonal to the velocity of the body, toward the instantaneous center of curvature of the path. The mathematical description was derived in 1659 by Dutch physicist Christiaan Huygens...
of circular motion
Circular motion
In physics, circular motion is rotation along a circular path or a circular orbit. It can be uniform, that is, with constant angular rate of rotation , or non-uniform, that is, with a changing rate of rotation. The rotation around a fixed axis of a three-dimensional body involves circular motion of...
. The first term is perpendicular to the radial direction, and pointing in the direction of travel. Its magnitude is 2sω, and it represents the acceleration of the walker as the edge of the carousel is neared, and the arc of circle traveled in a fixed time increases, as can be seen by the increased spacing between points for equal time steps on the spiral in Figure 5 as the outer edge of the carousel is approached.
Applying Newton's laws, multiplying the acceleration by the mass of the walker, the inertial observer concludes that the walker is subject to two forces: the inward, radially directed centripetal force, and another force perpendicular to the radial direction that is proportional to the speed of the walker.
Rotating observer
The rotating observer sees the walker travel a straight line from the center of the carousel to the periphery, as shown in Figure 5. Moreover, the rotating observer sees that the walker moves at a constant speed in the same direction, so applying Newton's law of inertia, there is zero force upon the walker. These conclusions do not agree with the inertial observer. To obtain agreement, the rotating observer has to introduce fictitious forces that appear to exist in the rotating world, even though there is no apparent reason for them, no apparent gravitational mass, electric charge or what have you, that could account for these fictitious forces.To agree with the inertial observer, the forces applied to the walker must be exactly those found above. They can be related to the general formulas already derived, namely:
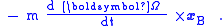
In this example, the velocity seen in the rotating frame is:
with uR a unit vector in the radial direction. The position of the walker as seen on the carousel is:
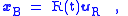
and the time derivative of Ω is zero for uniform angular rotation. Noticing that
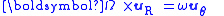
and
we find:
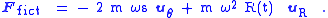
To obtain a straight-line motion in the rotating world, a force exactly opposite in sign to the fictitious force must be applied to reduce the net force on the walker to zero, so Newton's law of inertia will predict a straight line motion, in agreement with what the rotating observer sees. The fictitious forces that must be combated are the Coriolis force (first term) and the centrifugal force
Centrifugal force
Centrifugal force can generally be any force directed outward relative to some origin. More particularly, in classical mechanics, the centrifugal force is an outward force which arises when describing the motion of objects in a rotating reference frame...
(second term). (These terms are approximate.) By applying forces to counter these two fictitious forces, the rotating observer ends up applying exactly the same forces upon the walker that the inertial observer predicted were needed.
Because they differ only by the constant walking velocity, the walker and the rotational observer see the same accelerations. From the walker's perspective, the fictitious force is experienced as real, and combating this force is necessary to stay on a straight line radial path holding constant speed. It's like battling a crosswind while being thrown to the edge of the carousel.
Observation
Notice that this kinematicalKinematics
Kinematics is the branch of classical mechanics that describes the motion of bodies and systems without consideration of the forces that cause the motion....
discussion does not delve into the mechanism by which the required forces are generated. That is the subject of kinetics
Kinetics (physics)
In physics and engineering, kinetics is a term for the branch of classical mechanics that is concerned with the relationship between the motion of bodies and its causes, namely forces and torques...
. In the case of the carousel, the kinetic discussion would involve perhaps a study of the walker's shoes and the friction they need to generate against the floor of the carousel, or perhaps the dynamics of skateboarding, if the walker switched to travel by skateboard. Whatever the means of travel across the carousel, the forces calculated above must be realized. A very rough analogy is heating your house: you must have a certain temperature to be comfortable, but whether you heat by burning gas or by burning coal is another problem. Kinematics sets the thermostat, kinetics fires the furnace.
See also
- Newton's laws of motionNewton's laws of motionNewton's laws of motion are three physical laws that form the basis for classical mechanics. They describe the relationship between the forces acting on a body and its motion due to those forces...
- inertial reference frame
- non-inertial reference frameNon-inertial reference frameA non-inertial reference frame is a frame of reference that is under acceleration. The laws of physics in such a frame do not take on their most simple form, as required by the theory of special relativity...
- rotating reference frameRotating reference frameA rotating frame of reference is a special case of a non-inertial reference frame that is rotating relative to an inertial reference frame. An everyday example of a rotating reference frame is the surface of the Earth. A rotating frame of reference is a special case of a non-inertial reference...
- Coriolis force
- Centrifugal force
- Gravity
- General relativityGeneral relativityGeneral relativity or the general theory of relativity is the geometric theory of gravitation published by Albert Einstein in 1916. It is the current description of gravitation in modern physics...
- d'Alembert's principleD'Alembert's principleD'Alembert's principle, also known as the Lagrange–d'Alembert principle, is a statement of the fundamental classical laws of motion. It is named after its discoverer, the French physicist and mathematician Jean le Rond d'Alembert...
of inertial forces
- Centripetal forceCentripetal forceCentripetal force is a force that makes a body follow a curved path: it is always directed orthogonal to the velocity of the body, toward the instantaneous center of curvature of the path. The mathematical description was derived in 1659 by Dutch physicist Christiaan Huygens...
- Circular motionCircular motionIn physics, circular motion is rotation along a circular path or a circular orbit. It can be uniform, that is, with constant angular rate of rotation , or non-uniform, that is, with a changing rate of rotation. The rotation around a fixed axis of a three-dimensional body involves circular motion of...
- Uniform circular motionUniform circular motionIn physics, uniform circular motion describes the motion of a body traversing a circular path at constant speed. The distance of the body from the axis of rotation remains constant at all times. Though the body's speed is constant, its velocity is not constant: velocity, a vector quantity, depends...
- StaticsStaticsStatics is the branch of mechanics concerned with the analysis of loads on physical systems in static equilibrium, that is, in a state where the relative positions of subsystems do not vary over time, or where components and structures are at a constant velocity...
- Kinetics (physics)Kinetics (physics)In physics and engineering, kinetics is a term for the branch of classical mechanics that is concerned with the relationship between the motion of bodies and its causes, namely forces and torques...
- KinematicsKinematicsKinematics is the branch of classical mechanics that describes the motion of bodies and systems without consideration of the forces that cause the motion....
- Applied mechanicsApplied mechanicsApplied mechanics is a branch of the physical sciences and the practical application of mechanics. Applied mechanics examines the response of bodies or systems of bodies to external forces...
- Analytical mechanicsAnalytical mechanicsAnalytical mechanics is a term used for a refined, mathematical form of classical mechanics, constructed from the 18th century onwards as a formulation of the subject as founded by Isaac Newton. Often the term vectorial mechanics is applied to the form based on Newton's work, to contrast it with...
- Dynamics (physics)
- Classical mechanicsClassical mechanicsIn physics, classical mechanics is one of the two major sub-fields of mechanics, which is concerned with the set of physical laws describing the motion of bodies under the action of a system of forces...
- Generalized forces
- Generalized force
- Orthogonal coordinatesOrthogonal coordinatesIn mathematics, orthogonal coordinates are defined as a set of d coordinates q = in which the coordinate surfaces all meet at right angles . A coordinate surface for a particular coordinate qk is the curve, surface, or hypersurface on which qk is a constant...
- Curvilinear coordinatesCurvilinear coordinatesCurvilinear coordinates are a coordinate system for Euclidean space in which the coordinate lines may be curved. These coordinates may be derived from a set of Cartesian coordinates by using a transformation that is locally invertible at each point. This means that one can convert a point given...
- Generalized coordinatesGeneralized coordinatesIn the study of multibody systems, generalized coordinates are a set of coordinates used to describe the configuration of a system relative to some reference configuration....
- Frenet-Serret formulasFrenet-Serret formulasIn vector calculus, the Frenet–Serret formulas describe the kinematic properties of a particle which moves along a continuous, differentiable curve in three-dimensional Euclidean space R3...
External links
- Q and A from Richard C. Brill, Honolulu Community College
- NASA's David Stern: Lesson Plans for Teachers #23 on Inertial Forces
- Coriolis Force
- Motion over a flat surface Java physlet by Brian Fiedler illustrating fictitious forces. The physlet shows both the perspective as seen from a rotating and from a non-rotating point of view.
- Motion over a parabolic surface Java physlet by Brian Fiedler illustrating fictitious forces. The physlet shows both the perspective as seen from a rotating and as seen from a non-rotating point of view.