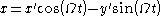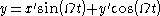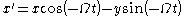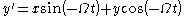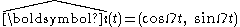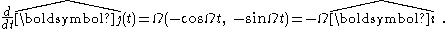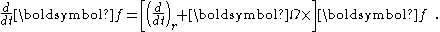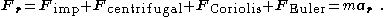Rotating reference frame
Encyclopedia
A rotating frame of reference is a special case of a non-inertial reference frame
that is rotating
relative to an inertial reference frame. An everyday example of a rotating reference frame is the surface of the Earth
. (This article considers only frames rotating about a fixed axis. For more general rotations, see Euler angles.)
s exhibit fictitious force
s. Rotating reference frames are characterized by three fictitious forces
and, for non-uniformly rotating reference frames,
Scientists living in a rotating box can measure the speed and direction of their rotation by measuring these fictitious force
s. For example, Léon Foucault
was able to show the Coriolis force that results from the Earth's rotation using the Foucault pendulum
. If the Earth were to rotate a thousandfold faster (making each day only ~86 seconds long), these fictitious forces could be felt as easily by humans, as they are when on a spinning carousel
.
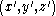of the rotating reference frame and the coordinates 
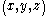of an inertial reference frame with the same origin. If the rotation is about the 
axis with an angular velocity
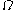and the two reference frames coincide at time 
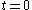, the transformation from rotating coordinates to inertial coordinates can be written
whereas the reverse transformation is
This result can be obtained from a rotation matrix.
Introduce the unit vectors
representing standard unit basis vectors in the rotating frame. The time-derivatives of these unit vectors are found next. Suppose the frames are aligned at t = 0 and the z-axis is the axis of rotation. Then for a counterclockwise rotation through angle Ωt:
where the (x, y) components are expressed in the stationary frame. Likewise,
Thus the time derivative of these vectors, which rotate without changing magnitude, is
This result is the same as found using a vector cross product with the rotation vector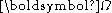
pointed along the z-axis of rotation 
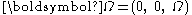, namely,
where
is either 
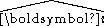or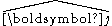 
.
representing standard unit basis vectors in the rotating frame. As they rotate they will remain normalized. If we let them rotate at the speed of 
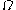about an axis 
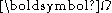then each unit vector 
of the rotating coordinate system abides by the following equation: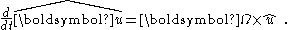
Then if we have a vector function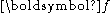
,
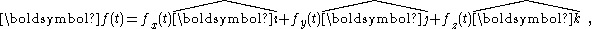
and we want to examine its first dervative we have (using the product rule
of differentiation):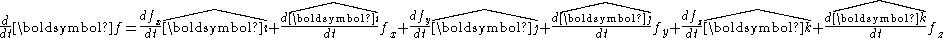
where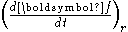
is the rate of change of 
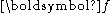as observed in the rotating coordinate system. As a shorthand the differentiation is expressed as:
This result is also known as the Transport Theorem in analytical dynamics, and is also sometimes referred to as the Basic Kinematic Equation.
The time derivative of a position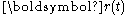
in a rotating reference frame has two components, one from the explicit time dependence due to motion of the particle itself, and another from the frame's own rotation. Applying the result of the previous subsection to the displacement 
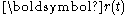, the velocities
in the two reference frames are related by the equation
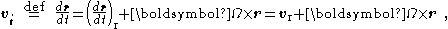
where subscript i means the inertial frame of reference, and r means the rotating frame of reference.
where subscript i means the inertial frame of reference.
Carrying out the differentiation
s and re-arranging some terms yields the acceleration in the rotating reference frame
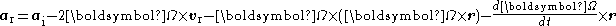
where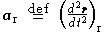
is the apparent acceleration in the rotating reference frame, the term 
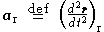represents centrifugal acceleration, and the term 
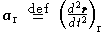is the coriolis effect
.
s in the rotating reference frame, that is, apparent forces that result from being in a non-inertial reference frame
, rather than from any physical interaction between bodies.
Using Newton's second law of motion
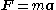, we obtain:
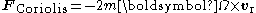
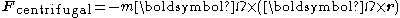
where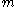
is the mass of the object being acted upon by these fictitious force
s. Notice that all three forces vanish when the frame is not rotating, that is, when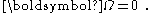
For completeness, the inertial acceleration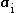
due to impressed external forces 
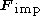can be determined from the total physical force in the inertial (non-rotating) frame (for example, force from physical interactions such as electromagnetic forces
) using Newton's second law
in the inertial frame:
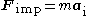
Newton's law in the rotating frame then becomes
In other words, to handle the laws of motion in a rotating reference frame:
, centrifugal force is an outward force associated with rotation
. Centrifugal force is one of several so-called pseudo-forces (also known as inertial forces), so named because, unlike real forces
, they do not originate in interactions with other bodies situated in the environment of the particle upon which they act. Instead, centrifugal force originates in the rotation of the frame of reference within which observations are made.
The mathematical expression for the Coriolis force appeared in an 1835 paper by a French scientist Gaspard-Gustave Coriolis
in connection with hydrodynamics, and also in the tidal equations
of Pierre-Simon Laplace
in 1778. Early in the 20th century, the term Coriolis force began to be used in connection with meteorology
.
Perhaps the most commonly encountered rotating reference frame is the Earth
. Moving objects on the surface of the Earth experience a Coriolis force, and appear to veer to the right in the northern hemisphere
, and to the left in the southern
. Movements of air in the atmosphere and water in the ocean are notable examples of this behavior: rather than flowing directly from areas of high pressure to low pressure, as they would on a non-rotating planet, winds and currents tend to flow to the right of this direction north of the equator
, and to the left of this direction south of the equator. This effect is responsible for the rotation of large cyclones (see Coriolis effects in meteorology).
, the Euler acceleration (named for Leonhard Euler
), also known as azimuthal acceleration or transverse acceleration is an acceleration
that appears when a non-uniformly rotating reference frame is used for analysis of motion and there is variation in the angular velocity
of the reference frame
's axis. This article is restricted to a frame of reference that rotates about a fixed axis.
The Euler force is a fictitious force
on a body that is related to the Euler acceleration by F = m a , where a is the Euler acceleration and m is the mass of the body.
Non-inertial reference frame
A non-inertial reference frame is a frame of reference that is under acceleration. The laws of physics in such a frame do not take on their most simple form, as required by the theory of special relativity...
that is rotating
Rotation
A rotation is a circular movement of an object around a center of rotation. A three-dimensional object rotates always around an imaginary line called a rotation axis. If the axis is within the body, and passes through its center of mass the body is said to rotate upon itself, or spin. A rotation...
relative to an inertial reference frame. An everyday example of a rotating reference frame is the surface of the Earth
Earth
Earth is the third planet from the Sun, and the densest and fifth-largest of the eight planets in the Solar System. It is also the largest of the Solar System's four terrestrial planets...
. (This article considers only frames rotating about a fixed axis. For more general rotations, see Euler angles.)
Fictitious forces
All non-inertial reference frameNon-inertial reference frame
A non-inertial reference frame is a frame of reference that is under acceleration. The laws of physics in such a frame do not take on their most simple form, as required by the theory of special relativity...
s exhibit fictitious force
Fictitious force
A fictitious force, also called a pseudo force, d'Alembert force or inertial force, is an apparent force that acts on all masses in a non-inertial frame of reference, such as a rotating reference frame....
s. Rotating reference frames are characterized by three fictitious forces
- the centrifugal force
- the Coriolis force
and, for non-uniformly rotating reference frames,
- the Euler forceEuler forceIn classical mechanics, the Euler acceleration , also known as azimuthal acceleration or transverse acceleration is an acceleration that appears when a non-uniformly rotating reference frame is used for analysis of motion and there is variation in the angular velocity of the reference frame's axes...
.
Scientists living in a rotating box can measure the speed and direction of their rotation by measuring these fictitious force
Fictitious force
A fictitious force, also called a pseudo force, d'Alembert force or inertial force, is an apparent force that acts on all masses in a non-inertial frame of reference, such as a rotating reference frame....
s. For example, Léon Foucault
Léon Foucault
Jean Bernard Léon Foucault was a French physicist best known for the invention of the Foucault pendulum, a device demonstrating the effect of the Earth's rotation...
was able to show the Coriolis force that results from the Earth's rotation using the Foucault pendulum
Foucault pendulum
The Foucault pendulum , or Foucault's pendulum, named after the French physicist Léon Foucault, is a simple device conceived as an experiment to demonstrate the rotation of the Earth. While it had long been known that the Earth rotated, the introduction of the Foucault pendulum in 1851 was the...
. If the Earth were to rotate a thousandfold faster (making each day only ~86 seconds long), these fictitious forces could be felt as easily by humans, as they are when on a spinning carousel
Carousel
A carousel , or merry-go-round, is an amusement ride consisting of a rotating circular platform with seats for riders...
.
Relating rotating frames to stationary frames
The following is a derivation of the formulas for accelerations as well as fictitious forces in a rotating frame. It begins with the relation between coordinates of the position of a particle in a rotating frame and the coordinates in an inertial (stationary) frame. Then, by taking time derivatives, formulas are derived that relate the velocity of the particle as seen in the two frames, and the acceleration relative to each frame. Using these accelerations a comparison of Newton's second law as formulated in the frames identifies the fictitious forces.Relation between positions in the two frames
To derive these fictitious forces, it's helpful to be able to convert between the coordinates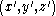 of the rotating reference frame and the coordinates 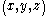of an inertial reference frame with the same origin. If the rotation is about the axis with an angular velocityAngular velocity
In physics, the angular velocity is a vector quantity which specifies the angular speed of an object and the axis about which the object is rotating. The SI unit of angular velocity is radians per second, although it may be measured in other units such as degrees per second, revolutions per...
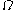and the two reference frames coincide at time 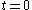, the transformation from rotating coordinates to inertial coordinates can be written
whereas the reverse transformation is
This result can be obtained from a rotation matrix.
Introduce the unit vectors
representing standard unit basis vectors in the rotating frame. The time-derivatives of these unit vectors are found next. Suppose the frames are aligned at t = 0 and the z-axis is the axis of rotation. Then for a counterclockwise rotation through angle Ωt:
where the (x, y) components are expressed in the stationary frame. Likewise,
Thus the time derivative of these vectors, which rotate without changing magnitude, is
This result is the same as found using a vector cross product with the rotation vector
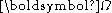pointed along the z-axis of rotation 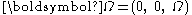, namely,
where
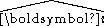is either or 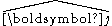.Time derivatives in the two frames
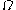Introduce the unit vectors representing standard unit basis vectors in the rotating frame. As they rotate they will remain normalized. If we let them rotate at the speed of about an axis 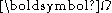then each unit vector of the rotating coordinate system abides by the following equation: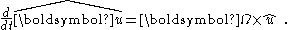Then if we have a vector function
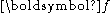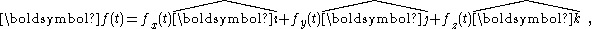
,and we want to examine its first dervative we have (using the product rule
Product rule
In calculus, the product rule is a formula used to find the derivatives of products of two or more functions. It may be stated thus:'=f'\cdot g+f\cdot g' \,\! or in the Leibniz notation thus:...
of differentiation):
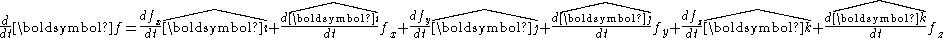
where
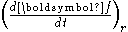is the rate of change of 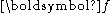as observed in the rotating coordinate system. As a shorthand the differentiation is expressed as:
This result is also known as the Transport Theorem in analytical dynamics, and is also sometimes referred to as the Basic Kinematic Equation.
Relation between velocities in the two frames
A velocity of an object is the time-derivative of the object's position, orThe time derivative of a position
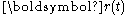in a rotating reference frame has two components, one from the explicit time dependence due to motion of the particle itself, and another from the frame's own rotation. Applying the result of the previous subsection to the displacement 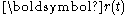, the velocitiesVelocity
In physics, velocity is speed in a given direction. Speed describes only how fast an object is moving, whereas velocity gives both the speed and direction of the object's motion. To have a constant velocity, an object must have a constant speed and motion in a constant direction. Constant ...
in the two reference frames are related by the equation
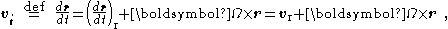
where subscript i means the inertial frame of reference, and r means the rotating frame of reference.
Relation between accelerations in the two frames
Acceleration is the second time derivative of position, or the first time derivative of velocitywhere subscript i means the inertial frame of reference.
Carrying out the differentiation
Derivative
In calculus, a branch of mathematics, the derivative is a measure of how a function changes as its input changes. Loosely speaking, a derivative can be thought of as how much one quantity is changing in response to changes in some other quantity; for example, the derivative of the position of a...
s and re-arranging some terms yields the acceleration in the rotating reference frame
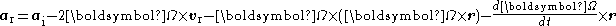
where
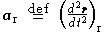is the apparent acceleration in the rotating reference frame, the term 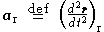represents centrifugal acceleration, and the term 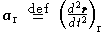is the coriolis effectCoriolis effect
In physics, the Coriolis effect is a deflection of moving objects when they are viewed in a rotating reference frame. In a reference frame with clockwise rotation, the deflection is to the left of the motion of the object; in one with counter-clockwise rotation, the deflection is to the right...
.
Newton's second law in the two frames
When the expression for acceleration is multiplied by the mass of the particle, the three extra terms on the right-hand side result in fictitious forceFictitious force
A fictitious force, also called a pseudo force, d'Alembert force or inertial force, is an apparent force that acts on all masses in a non-inertial frame of reference, such as a rotating reference frame....
s in the rotating reference frame, that is, apparent forces that result from being in a non-inertial reference frame
Non-inertial reference frame
A non-inertial reference frame is a frame of reference that is under acceleration. The laws of physics in such a frame do not take on their most simple form, as required by the theory of special relativity...
, rather than from any physical interaction between bodies.
Using Newton's second law of motion
Newton's laws of motion
Newton's laws of motion are three physical laws that form the basis for classical mechanics. They describe the relationship between the forces acting on a body and its motion due to those forces...
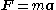, we obtain:- the Coriolis force
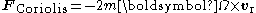
- the centrifugal force
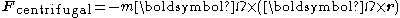
- and the Euler forceEuler forceIn classical mechanics, the Euler acceleration , also known as azimuthal acceleration or transverse acceleration is an acceleration that appears when a non-uniformly rotating reference frame is used for analysis of motion and there is variation in the angular velocity of the reference frame's axes...
where
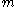is the mass of the object being acted upon by these fictitious forceFictitious force
A fictitious force, also called a pseudo force, d'Alembert force or inertial force, is an apparent force that acts on all masses in a non-inertial frame of reference, such as a rotating reference frame....
s. Notice that all three forces vanish when the frame is not rotating, that is, when
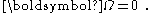
For completeness, the inertial acceleration
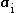due to impressed external forces 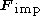can be determined from the total physical force in the inertial (non-rotating) frame (for example, force from physical interactions such as electromagnetic forcesElectromagnetism
Electromagnetism is one of the four fundamental interactions in nature. The other three are the strong interaction, the weak interaction and gravitation...
) using Newton's second law
Newton's laws of motion
Newton's laws of motion are three physical laws that form the basis for classical mechanics. They describe the relationship between the forces acting on a body and its motion due to those forces...
in the inertial frame:
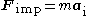
Newton's law in the rotating frame then becomes
In other words, to handle the laws of motion in a rotating reference frame:
Centrifugal force
In classical mechanicsClassical mechanics
In physics, classical mechanics is one of the two major sub-fields of mechanics, which is concerned with the set of physical laws describing the motion of bodies under the action of a system of forces...
, centrifugal force is an outward force associated with rotation
Rotation
A rotation is a circular movement of an object around a center of rotation. A three-dimensional object rotates always around an imaginary line called a rotation axis. If the axis is within the body, and passes through its center of mass the body is said to rotate upon itself, or spin. A rotation...
. Centrifugal force is one of several so-called pseudo-forces (also known as inertial forces), so named because, unlike real forces
Fundamental interaction
In particle physics, fundamental interactions are the ways that elementary particles interact with one another...
, they do not originate in interactions with other bodies situated in the environment of the particle upon which they act. Instead, centrifugal force originates in the rotation of the frame of reference within which observations are made.
Coriolis effect
Gaspard-Gustave Coriolis
Gaspard-Gustave de Coriolis or Gustave Coriolis was a French mathematician, mechanical engineer and scientist. He is best known for his work on the supplementary forces that are detected in a rotating frame of reference. See the Coriolis Effect...
in connection with hydrodynamics, and also in the tidal equations
Theory of tides
The theory of tides is the application of continuum mechanics to interpret and predict the tidal deformations of planetary and satellite bodies and their atmospheres and oceans, under the gravitational loading of another astronomical body or bodies...
of Pierre-Simon Laplace
Pierre-Simon Laplace
Pierre-Simon, marquis de Laplace was a French mathematician and astronomer whose work was pivotal to the development of mathematical astronomy and statistics. He summarized and extended the work of his predecessors in his five volume Mécanique Céleste...
in 1778. Early in the 20th century, the term Coriolis force began to be used in connection with meteorology
Meteorology
Meteorology is the interdisciplinary scientific study of the atmosphere. Studies in the field stretch back millennia, though significant progress in meteorology did not occur until the 18th century. The 19th century saw breakthroughs occur after observing networks developed across several countries...
.
Perhaps the most commonly encountered rotating reference frame is the Earth
Earth
Earth is the third planet from the Sun, and the densest and fifth-largest of the eight planets in the Solar System. It is also the largest of the Solar System's four terrestrial planets...
. Moving objects on the surface of the Earth experience a Coriolis force, and appear to veer to the right in the northern hemisphere
Northern Hemisphere
The Northern Hemisphere is the half of a planet that is north of its equator—the word hemisphere literally means “half sphere”. It is also that half of the celestial sphere north of the celestial equator...
, and to the left in the southern
Southern Hemisphere
The Southern Hemisphere is the part of Earth that lies south of the equator. The word hemisphere literally means 'half ball' or "half sphere"...
. Movements of air in the atmosphere and water in the ocean are notable examples of this behavior: rather than flowing directly from areas of high pressure to low pressure, as they would on a non-rotating planet, winds and currents tend to flow to the right of this direction north of the equator
Equator
An equator is the intersection of a sphere's surface with the plane perpendicular to the sphere's axis of rotation and containing the sphere's center of mass....
, and to the left of this direction south of the equator. This effect is responsible for the rotation of large cyclones (see Coriolis effects in meteorology).
Euler force
In classical mechanicsClassical mechanics
In physics, classical mechanics is one of the two major sub-fields of mechanics, which is concerned with the set of physical laws describing the motion of bodies under the action of a system of forces...
, the Euler acceleration (named for Leonhard Euler
Leonhard Euler
Leonhard Euler was a pioneering Swiss mathematician and physicist. He made important discoveries in fields as diverse as infinitesimal calculus and graph theory. He also introduced much of the modern mathematical terminology and notation, particularly for mathematical analysis, such as the notion...
), also known as azimuthal acceleration or transverse acceleration is an acceleration
Acceleration
In physics, acceleration is the rate of change of velocity with time. In one dimension, acceleration is the rate at which something speeds up or slows down. However, since velocity is a vector, acceleration describes the rate of change of both the magnitude and the direction of velocity. ...
that appears when a non-uniformly rotating reference frame is used for analysis of motion and there is variation in the angular velocity
Angular velocity
In physics, the angular velocity is a vector quantity which specifies the angular speed of an object and the axis about which the object is rotating. The SI unit of angular velocity is radians per second, although it may be measured in other units such as degrees per second, revolutions per...
of the reference frame
Frame of reference
A frame of reference in physics, may refer to a coordinate system or set of axes within which to measure the position, orientation, and other properties of objects in it, or it may refer to an observational reference frame tied to the state of motion of an observer.It may also refer to both an...
's axis. This article is restricted to a frame of reference that rotates about a fixed axis.
The Euler force is a fictitious force
Fictitious force
A fictitious force, also called a pseudo force, d'Alembert force or inertial force, is an apparent force that acts on all masses in a non-inertial frame of reference, such as a rotating reference frame....
on a body that is related to the Euler acceleration by F = m a , where a is the Euler acceleration and m is the mass of the body.
See also
- Absolute rotation
- Centrifugal force (rotating reference frame) Centrifugal force as seen from systems rotating about a fixed axis
- Mechanics of planar particle motionMechanics of planar particle motionThis article describes a particle in planar motion when observed from non-inertial reference frames. The most famous examples of planar motion are related to the motion of two spheres that are gravitationally attracted to one another, and the generalization of this problem to planetary motion....
Fictitious forces exhibited by a particle in planar motion as seen by the particle itself and by observers in a co-rotating frame of reference - Coriolis force The effect of the Coriolis force on the Earth and other rotating systems
- Inertial frame of referenceInertial frame of referenceIn physics, an inertial frame of reference is a frame of reference that describes time homogeneously and space homogeneously, isotropically, and in a time-independent manner.All inertial frames are in a state of constant, rectilinear motion with respect to one another; they are not...
- Non-inertial frame
- Fictitious forceFictitious forceA fictitious force, also called a pseudo force, d'Alembert force or inertial force, is an apparent force that acts on all masses in a non-inertial frame of reference, such as a rotating reference frame....
A more general treatment of the subject of this article
External links
- Animation clip showing scenes as viewed from both an inertial frame and a rotating frame of reference, visualizing the Coriolis and centrifugal forces.