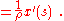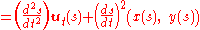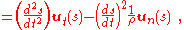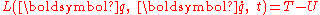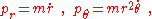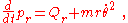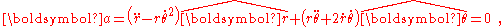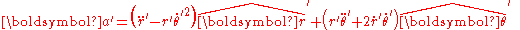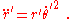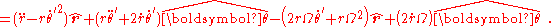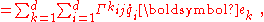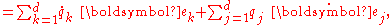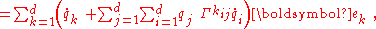Mechanics of planar particle motion
Encyclopedia
This article describes a particle in planar motion when observed from non-inertial reference frames. The most famous examples of planar motion are related to the motion of two spheres that are gravitationally attracted to one another, and the generalization of this problem to planetary motion. See centrifugal force, two-body problem
, orbit
and Kepler's laws of planetary motion
. Those problems fall in the general field of analytical dynamics
, the determination of orbits from given laws of force. This article is focused more on the kinematical
issues surrounding planar motion, that is, determination of the forces necessary to result in a certain trajectory given the particle trajectory.
General results presented in fictitious force
s here are applied to observations of a moving particle as seen from several specific non-inertial frames, for example, a local frame (one tied to the moving particle so it appears stationary), and a co-rotating frame (one with an arbitrarily located but fixed axis and a rate of rotation that makes the particle appear to have only radial motion and zero azimuthal motion). The Lagrangian approach to fictitious forces is introduced.
Unlike real force
s such as electromagnetic forces, fictitious forces do not originate from physical interactions between objects.
. The connection between inertial frames and fictitious force
s (also called inertial forces or pseudo-forces), is expressed, for example, by Arnol'd:
A slightly different tack on the subject is provided by Iro:
Fictitious forces do not appear in the equations of motion
in an inertial frame of reference
: in an inertial frame, the motion of an object is explained by the real impressed forces. In a non-inertial frame such as a rotating frame, however, Newton's first and second laws still can be used to make accurate physical predictions provided fictitious forces are included along with the real forces. For solving problems of mechanics in non-inertial reference frames, the advice given in textbooks is to treat the fictitious forces like real forces and to pretend you are in an inertial frame.
It should be mentioned that "treating the fictitious forces like real forces" means, in particular, that fictitious forces as seen in a particular non-inertial frame transform as vectors under coordinate transformations made within that frame, that is, like real forces.
is used often in a very broad sense, but for the present discussion its meaning is restricted to refer to an observer's state of motion, that is, to either an inertial frame of reference or a non-inertial frame of reference.
The term coordinate system
is used to differentiate between different possible choices for a set of variables to describe motion, choices available to any observer, regardless of their state of motion. Examples are Cartesian coordinates, polar coordinates and (more generally) curvilinear coordinates
.
Here are two quotes relating "state of motion" and "coordinate system":
In discussion of a particle moving in a circular orbit, in an inertial frame of reference one can identify the centripetal and tangential forces. It then seems to be no problem to switch hats, change perspective, and talk about the fictitious forces commonly called the centrifugal and Euler force
. But what underlies this switch in vocabulary is a change of observational frame of reference from the inertial frame where we started, where centripetal and tangential forces make sense, to a rotating frame of reference where the particle appears motionless and fictitious centrifugal and Euler forces have to be brought into play. That switch is unconscious, but real.
Suppose we sit on a particle in general planar motion (not just a circular orbit). What analysis underlies a switch of hats to introduce fictitious centrifugal and Euler forces?
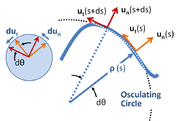
To explore that question, begin in an inertial frame of reference. By using a coordinate system commonly used in planar motion, the so-called local coordinate system, as shown in Figure 1, it becomes easy to identify formulas for the centripetal inward force normal to the trajectory (in direction opposite to un in Figure 1), and the tangential force parallel to the trajectory (in direction ut), as shown next.
To introduce the unit vectors of the local coordinate system shown in Figure 1, one approach is to begin in Cartesian coordinates in an inertial framework and describe the local coordinates in terms of these Cartesian coordinates. In Figure 1, the arc length
s is the distance the particle has traveled along its path in time t. The path r (t) with components x(t), y(t) in Cartesian coordinates is described using arc length s(t) as: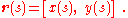
]
One way to look at the use of s is to think of the path of the particle as sitting in space, like the trail left by a skywriter
, independent of time. Any position on this path is described by stating its distance s from some starting point on the path. Then an incremental displacement along the path ds is described by: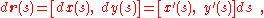
where primes are introduced to denote derivatives with respect to s. The magnitude of this displacement is ds, showing that: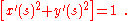
(Eq. 1)
This displacement is necessarily tangent to the curve at s, showing that the unit vector tangent to the curve is:
while the outward unit vector normal to the curve is
Orthogonality can be verified by showing the vector dot product
is zero. The unit magnitude of these vectors is a consequence of Eq. 1.
As an aside, notice that the use of unit vectors that are not aligned along the Cartesian xy-axes does not mean we are no longer in an inertial frame. All it means is that we are using unit vectors that vary with s to describe the path, but still observe the motion from the inertial frame.
Using the tangent vector, the angle of the tangent to the curve, say θ, is given by: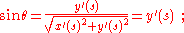
and 
The radius of curvature is introduced completely formally (without need for geometric interpretation) as: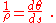
The derivative of θ can be found from that for sin θ:
Now:
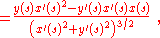
in which the denominator is unity according to Eq. 1. With this formula for the derivative of the sine, the radius of curvature becomes: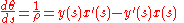
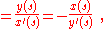
where the equivalence of the forms stems from differentiation of Eq. 1: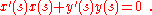
Having set up the description of any position on the path in terms of its associated value for s, and having found the properties of the path in terms of this description, motion of the particle is introduced by stating the particle position at any time t as the corresponding value s (t).
Using the above results for the path properties in terms of s, the acceleration in the inertial reference frame as described in terms of the components normal and tangential to the path of the particle can be found in terms of the function s(t) and its various time derivatives (as before, primes indicate differentiation with respect to s):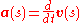
as can be verified by taking the dot product with the unit vectors ut(s) and un(s). This result for acceleration is the same as that for circular motion based on the radius ρ. Using this coordinate system in the inertial frame, it is easy to identify the force normal to the trajectory as the centripetal force and that parallel to the trajectory as the tangential force.
Next, we change observational frames. Sitting on the particle, we adopt a non-inertial frame where the particle is at rest (zero velocity). This frame has a continuously changing origin, which at time t is the center of curvature (the center of the osculating circle
in Figure 1) of the path at time t, and whose rate of rotation is the angular rate of motion of the particle about that origin at time t. This non-inertial frame also employs unit vectors normal to the trajectory and parallel to it.
The angular velocity
of this frame is the angular velocity of the particle about the center of curvature at time t. The centripetal force of the inertial frame is interpreted in the non-inertial frame where the body is at rest as a force necessary to overcome the centrifugal force. Likewise, the force causing any acceleration of speed along the path seen in the inertial frame becomes the force necessary to overcome the Euler force in the non-inertial frame where the particle is at rest. There is zero Coriolis force in the frame, because the particle has zero velocity in this frame. For a pilot in an airplane, for example, these fictitious forces are a matter of direct experience. However, these fictitious forces cannot be related to a simple observational frame of reference other than the particle itself, unless it is in a particularly simple path, like a circle.
That said, from a qualitative standpoint, the path of an airplane can be approximated by an arc of a circle for a limited time, and for the limited time a particular radius of curvature applies, the centrifugal and Euler forces can be analyzed on the basis of circular motion with that radius. See article discussing turning an airplane.
Next, reference frames rotating about a fixed axis are discussed in more detail.
which contains not just double time derivatives of the coordinates but added terms. This example employs polar coordinates, but more generally the added terms depend upon which coordinate system is chosen (that is, polar, elliptic, or whatever).
Sometimes these coordinate-system dependent terms also are referred to as "fictitious forces", introducing a second meaning for "fictitious forces", despite the fact that these terms do not have the vector transformation properties
expected of forces. For example, see Shankar and Hildebrand. According to this terminology, fictitious forces are determined in part by the coordinate system itself, regardless of the frame it is attached to, that is, regardless of whether the coordinate system is attached to an inertial or a non-inertial frame of reference. In contrast, the fictitious forces defined in terms of the state of motion of the observer vanish in inertial frames of reference. To distinguish these two terminologies, the fictitious forces that vanish in an inertial frame of reference, the inertial forces of Newtonian mechanics, are called in this article the "state-of-motion" fictitious forces and those that originate in the interpretation of time derivatives in particular coordinate systems are called "coordinate" fictitious forces.
Assuming it is clear that "state of motion" and "coordinate system" are different, it follows that the dependence of centrifugal force (as in this article) upon "state of motion" and its independence from "coordinate system", which contrasts with the "coordinate" version with exactly the opposite dependencies, indicates that two different ideas are referred to by the terminology "fictitious force". The present article emphasizes one of these two ideas ("state-of-motion"), although the other also is described.
Below, polar coordinates are introduced for use in (first) an inertial frame of reference and then (second) in a rotating frame of reference. The two different uses of the term "fictitious force" are pointed out. First, however, follows a brief digression to explain further how the "coordinate" terminology for fictitious force has arisen.
approach to mechanics based upon describing a system by generalized coordinates usually denoted as {qk}. The only requirement on these coordinates is that they are necessary and sufficient to uniquely characterize the state of the system: they need not be (although they could be) the coordinates of the particles in the system. Instead, they could be the angles and extensions of links in a robot arm, for instance. If a mechanical system consists of N particles and there are m independent kinematical conditions imposed, it is possible to characterize the system uniquely by n = 3N - m independent generalized coordinates
{qk}.
In classical mechanics, the Lagrangian is defined as the kinetic energy
,
, of the system minus its potential energy
,
. In symbols,
Under conditions that are given in Lagrangian mechanics
, if the Lagrangian of a system is known, then the equations of motion
of the system may be obtained by a direct substitution of the expression for the Lagrangian into the Euler–Lagrange equation, a particular family of partial differential equation
s.
Here are some definitions:
It is not the purpose here to outline how Lagrangian mechanics works. The interested reader can look at other articles explaining this approach. For the moment, the goal is simply to show that the Lagrangian approach can lead to "generalized fictitious forces" that do not vanish in inertial frames. What is pertinent here is that in the case of a single particle, the Lagrangian approach can be arranged to capture exactly the "coordinate" fictitious forces just introduced.
To proceed, consider a single particle, and introduce the generalized coordinates as {qk} = (r, θ). Then Hildebrand shows in polar coordinates with the qk = (r, θ) the "generalized momenta" are:
leading, for example, to the generalized force:
with Qr the impressed radial force. The connection between "generalized forces" and Newtonian forces varies with the choice of coordinates. This Lagrangian formulation introduces exactly the "coordinate" form of fictitious forces mentioned above that allows "fictitious" (generalized) forces in inertial frames, for example, the term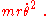
Careful reading of Hildebrand shows he doesn't discuss the role of "inertial frames of reference", and in fact, says "[The] presence or absence [of inertia forces] depends, not upon the particular problem at hand but upon the coordinate system chosen." By coordinate system presumably is meant the choice of {qk}. Later he says "If accelerations associated with generalized coordinates are to be of prime interest (as is usually the case), the [nonaccelerational] terms may be conveniently transferred to the right … and considered as additional (generalized) inertia forces. Such inertia forces are often said to be of the Coriolis type."
In short, the emphasis of some authors upon coordinates and their derivatives and their introduction of (generalized) fictitious forces that do not vanish in inertial frames of reference is an outgrowth of the use of generalized coordinates
in Lagrangian mechanics
. For example, see McQuarrie Hildebrand, and von Schwerin. Below is an example of this usage as employed in the design of robotic manipulators:
For a robot manipulator, the equations may be written in a form using Christoffel symbols
Γijk (discussed further below) as:
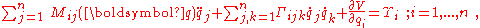
where M is the "manipulator inertia matrix" and V is the potential energy due to gravity (for example), and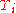
are the generalized forces on joint i. The terms involving Christoffel symbols therefore determine the "generalized centrifugal" and "generalized Coriolis" terms.
The introduction of generalized fictitious forces often is done without notification and without specifying the word "generalized". This sloppy use of terminology leads to endless confusion because these generalized fictitious forces, unlike the standard "state-of-motion" fictitious forces, do not vanish in inertial frames of reference.
In an inertial frame, let
be the position vector of a moving particle. Its Cartesian components (x, y) are:
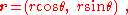
with polar coordinates r and θ depending on time t.
Unit vectors are defined in the radially outward direction
:
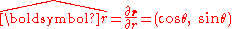
and in the direction at right angles to
:
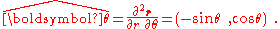
These unit vectors vary in direction with time:
and:
Using these derivatives, the first and second derivatives of position are:
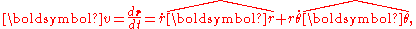
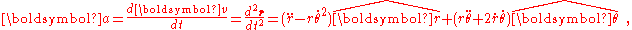
where dot-overmarkings indicate time differentiation. With this form for the acceleration
, in an inertial frame of reference Newton's second law expressed in polar coordinates is: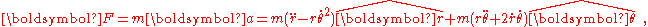
where F is the net real force on the particle. No fictitious forces appear because all fictitious forces are zero by definition in an inertial frame.
From a mathematical standpoint, however, it sometimes is handy to put only the second-order derivatives on the right side of this equation; that is we write the above equation by rearrangement of terms as: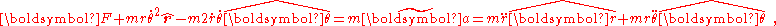
where a "coordinate" version of the "acceleration" is introduced:
consisting of only second-order time derivatives of the coordinates r and θ. The terms moved to the force-side of the equation are now treated as extra "fictitious forces" and, confusingly, the resulting forces also are called the "centrifugal" and "Coriolis" force.
These newly defined "forces" are non-zero in an inertial frame, and so certainly are not the same as the previously identified fictitious forces that are zero in an inertial frame and non-zero only in a non-inertial frame. In this article, these newly defined forces are called the "coordinate" centrifugal force and the "coordinate" Coriolis force to separate them from the "state-of-motion" forces.
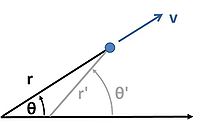
does not transform as a true force, putting any reference to this term not just as a "term", but as a centrifugal force, in a dubious light. Suppose in frame S a particle moves radially away from the origin at a constant velocity. See Figure 2. The force on the particle is zero by Newton's first law. Now we look at the same thing from frame S' , which is the same, but displaced in origin. In S' the particle still is in straight line motion at constant speed, so again the force is zero.
What if we use polar coordinates in the two frames? In frame S the radial motion is constant and there is no angular motion. Hence, the acceleration is:
and each term individually is zero because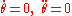
and 
. There is no force, including no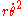 
"force" in frame S.
In frame S' , however, we have:
In this case the azimuthal term is zero, being the rate of change of angular momentum. To obtain zero acceleration in the radial direction, however, we require:
The right-hand side is non-zero, inasmuch as neither
nor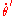 
is zero. That is, we cannot obtain zero force (zero 
) if we retain only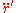 
as the acceleration; we need both terms.
Despite the above facts, suppose we adopt polar coordinates, and wish to say that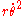
is "centrifugal force", and reinterpret 
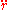as "acceleration" (without dwelling upon any possible justification). How does this decision fare when we consider that a proper formulation of physics is geometry and coordinate-independent? See the article on general covariance
. To attempt to form a covariant expression, this so-called centrifugal "force" can be put into vector notation as:
with:
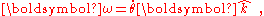
and
a unit vector normal to the plane of motion. Unfortunately, although this expression formally looks like a vector, when an observer changes origin the value of 
changes (see Figure 2), so observers in the same frame of reference standing on different street corners see different "forces" even though the actual events they witness are identical.
How can a physical force (be it fictitious or real) be zero in one frame S, but non-zero in another frame S' identical, but a few feet away? Even for exactly the same particle behavior the expression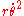
is different in every frame of reference, even for very trivial distinctions between frames. In short, if we take 
as "centrifugal force", it does not have a universal significance: it is unphysical.
Beyond this problem, the real impressed net force is zero. (There is no real impressed force in straight-line motion at constant speed). If we adopt polar coordinates, and wish to say that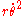
is "centrifugal force", and reinterpret 
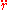as "acceleration", the oddity results in frame S' that straight-line motion at constant speed requires a net force in polar coordinates, but not in Cartesian coordinates. Moreover, this perplexity applies in frame S, but not in frame S.
The absurdity of the behavior of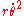
indicates that one must say that 
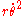is not centrifugal force, but simply one of two terms in the acceleration. This view, that the acceleration is composed of two terms, is frame-independent: there is zero centrifugal force in any and every inertial frame. It also is coordinate-system independent: we can use Cartesian, polar, or any other curvilinear system: they all produce zero.
Apart from the above physical arguments, of course, the derivation above, based upon application of the mathematical rules of differentiation, shows the radial acceleration does indeed consist of the two terms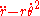
.
That said, the next subsection shows there is a connection between these centrifugal and Coriolis terms and the fictitious forces that pertain to a particular rotating frame of reference (as distinct from an inertial frame).
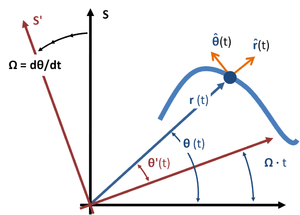
Consequently,
Plugging this result into the acceleration using the unit vectors of the previous section: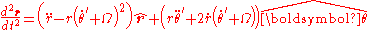
The leading two terms are the same form as those in the inertial frame, and they are the only terms if the frame is not rotating, that is, if Ω=0. However, in this rotating frame we have the extra terms:
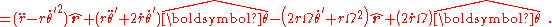
The radial term Ω2 r is the centrifugal force per unit mass due to the system's rotation at rate Ω and the radial term
is the radial component of the Coriolis force per unit mass, where 
is the tangential component of the particle velocity as seen in the rotating frame. The term 
is the so-called azimuthal component of the Coriolis force per unit mass. In fact, these extra terms can be used to measure Ω and provide a test to see whether or not the frame is rotating, just as explained in the example of rotating identical spheres
. If the particle's motion can be described by the observer using Newton's laws of motion without these Ω-dependent terms, the observer is in an inertial frame of reference
where Ω=0.
These "extra terms" in the acceleration of the particle are the "state of motion" fictitious forces for this rotating frame, the forces introduced by rotation of the frame at angular rate Ω.
In this rotating frame, what are the "coordinate" fictitious forces? As before, suppose we choose to put only the second-order time derivatives on the right side of Newton's law: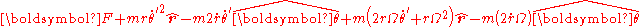
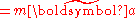
If we choose for convenience to treat
as some so-called "acceleration", then the terms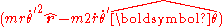 
are added to the so-called "fictitious force", which are not "state-of-motion" fictitious forces, but are actually components of force that persist even when Ω=0, that is, they persist even in an inertial frame of reference. Because these extra terms are added, the "coordinate" fictitious force is not the same as the "state-of-motion" fictitious force. Because of these extra terms, the "coordinate" fictitious force is not zero even in an inertial frame of reference.
To quote Bullo and Lewis: "Only in exceptional circumstances can the configuration of Lagrangian system be described by a vector in a vector space. In the natural mathematical setting, the system's configuration space is described loosely as a curved space, or more accurately as a differentiable manifold
."
Instead of Cartesian coordinates, when equations of motion are expressed in a curvilinear coordinate
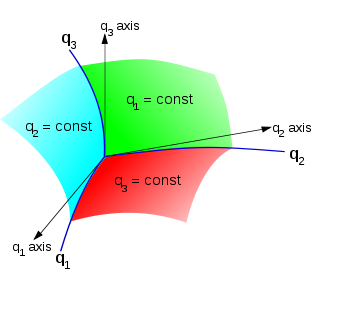
system, Christoffel symbols appear in the acceleration of a particle expressed in this coordinate system, as described below in more detail. Consider description of a particle motion from the viewpoint of an inertial frame of reference in curvilinear coordinates. Suppose the position of a point P in Cartesian coordinates is (x, y, z) and in curvilinear coordinates is (q1, q2. q3). Then functions exist that relate these descriptions: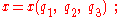
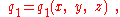
and so forth. (The number of dimensions may be larger than three.) An important aspect of such coordinate systems is the element of arc length that allows distances to be determined. If the curvilinear coordinates form an orthogonal coordinate
system, the element of arc length ds is expressed as: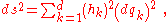
where the quantities hk are called scale factors. A change dqk in qk causes a displacement hk dqk along the coordinate line for qk. At a point P, we place unit vectors ek each tangent to a coordinate line of a variable qk. Then any vector can be expressed in terms of these basis vectors, for example, from an inertial frame of reference, the position vector of a moving particle r located at time t at position P becomes:
where qk is the vector dot product
of r and ek.
The velocity v of a particle at P, can be expressed at P as: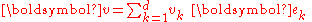
where vk is the vector dot product
of v and ek, and over dots indicate time differentiation.
The time derivatives of the basis vectors can be expressed in terms of the scale factors introduced above. for example: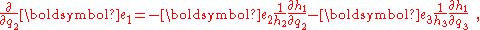
or, in general,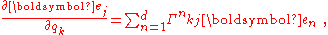 
in which the coefficients of the unit vectors are the Christoffel symbols
for the coordinate system. The general notation and formulas for the Christoffel symbols are: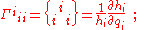
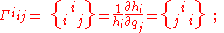
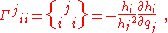
and the symbol is zero when all the indices are different. Despite appearances to the contrary, the Christoffel symbols do not form the components of a tensor. For example, they are zero in Cartesian coordinates, but not in polar coordinates.
Using relations like this one,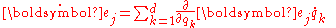
which allows all the time derivatives to be evaluated. For example, for the velocity: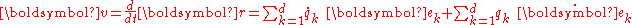
with the Γ-notation for the Christoffel symbols replacing the curly bracket notation.
Using the same approach, the acceleration is then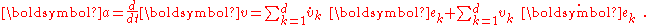
Looking at the relation for acceleration, the first summation contains the time derivatives of velocity, which would be associated with acceleration if these were Cartesian coordinates, and the second summation (the one with Christoffel symbols) contains terms related to the way the unit vectors change with time.
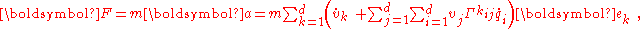
where F is the net real force on the particle. No "state-of-motion" fictitious forces are present because the frame is inertial, and "state-of-motion" fictitious forces are zero in an inertial frame, by definition.
The "coordinate" approach to Newton's law above is to retain the second-order time derivatives of the coordinates {qk} as the only terms on the right side of this equation, motivated more by mathematical convenience than by physics. To that end, the force law can be rewritten, taking the second summation to the force-side of the equation as: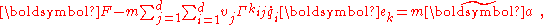
with the convention that the "acceleration"
is now:
In the expression above, the summation added to the force-side of the equation now is treated as if added "forces" were present. These summation terms are customarily called fictitious forces within this "coordinate" approach, although in this inertial frame of reference all "state-of-motion" fictitious forces are identically zero. Moreover, these "forces" do not transform under coordinate transformations as vectors. Thus, the designation of the terms of the summation as "fictitious forces" uses this terminology for contributions that are completely different from any real force, and from the "state-of-motion" fictitious forces. What adds to this confusion is that these "coordinate" fictitious forces are divided into two groups and given the same names as the "state-of-motion" fictitious forces, that is, they are divided into "centrifugal" and "Coriolis" terms, despite their inclusion of terms that are not the "state-of-motion" centrifugal and Coriolis terms. For example, these "coordinate" centrifugal and Coriolis terms can be nonzero even in an inertial frame of reference where the "state-of-motion" centrifugal force (the subject of this article) and Coriolis force always are zero.
If the frame is not inertial, for example, in a rotating frame of reference, the "state-of-motion" fictitious forces are included in the above "coordinate" fictitious force expression. Also, if the "acceleration" expressed in terms of first-order time derivatives of the velocity happens to result in terms that are not simply second-order derivatives of the coordinates {qk} in time, then these terms that are not second-order also are brought to the force-side of the equation and included with the fictitious forces. From the standpoint of a Lagrangian formulation, they can be called generalized fictitious forces. See Hildebrand , for example.
Formulation of dynamics in terms of Christoffel symbols and the "coordinate" version of fictitious forces is used often in the design of robots
in connection with a Lagrangian formulation
of the equations of motion.
Two-body problem
In classical mechanics, the two-body problem is to determine the motion of two point particles that interact only with each other. Common examples include a satellite orbiting a planet, a planet orbiting a star, two stars orbiting each other , and a classical electron orbiting an atomic nucleus In...
, orbit
Orbit
In physics, an orbit is the gravitationally curved path of an object around a point in space, for example the orbit of a planet around the center of a star system, such as the Solar System...
and Kepler's laws of planetary motion
Kepler's laws of planetary motion
In astronomy, Kepler's laws give a description of the motion of planets around the Sun.Kepler's laws are:#The orbit of every planet is an ellipse with the Sun at one of the two foci....
. Those problems fall in the general field of analytical dynamics
Analytical dynamics
In classical mechanics, analytical dynamics, or more briefly dynamics, is concerned about the relationship between motion of bodies and its causes, namely the forces acting on the bodies and the properties of the bodies...
, the determination of orbits from given laws of force. This article is focused more on the kinematical
Kinematics
Kinematics is the branch of classical mechanics that describes the motion of bodies and systems without consideration of the forces that cause the motion....
issues surrounding planar motion, that is, determination of the forces necessary to result in a certain trajectory given the particle trajectory.
General results presented in fictitious force
Fictitious force
A fictitious force, also called a pseudo force, d'Alembert force or inertial force, is an apparent force that acts on all masses in a non-inertial frame of reference, such as a rotating reference frame....
s here are applied to observations of a moving particle as seen from several specific non-inertial frames, for example, a local frame (one tied to the moving particle so it appears stationary), and a co-rotating frame (one with an arbitrarily located but fixed axis and a rate of rotation that makes the particle appear to have only radial motion and zero azimuthal motion). The Lagrangian approach to fictitious forces is introduced.
Unlike real force
Force
In physics, a force is any influence that causes an object to undergo a change in speed, a change in direction, or a change in shape. In other words, a force is that which can cause an object with mass to change its velocity , i.e., to accelerate, or which can cause a flexible object to deform...
s such as electromagnetic forces, fictitious forces do not originate from physical interactions between objects.
Analysis using fictitious forces
The appearance of fictitious forces normally is associated with use of a non-inertial frame of reference, and their absence with use of an inertial frame of referenceInertial frame of reference
In physics, an inertial frame of reference is a frame of reference that describes time homogeneously and space homogeneously, isotropically, and in a time-independent manner.All inertial frames are in a state of constant, rectilinear motion with respect to one another; they are not...
. The connection between inertial frames and fictitious force
Fictitious force
A fictitious force, also called a pseudo force, d'Alembert force or inertial force, is an apparent force that acts on all masses in a non-inertial frame of reference, such as a rotating reference frame....
s (also called inertial forces or pseudo-forces), is expressed, for example, by Arnol'd:
A slightly different tack on the subject is provided by Iro:
Fictitious forces do not appear in the equations of motion
Newton's laws of motion
Newton's laws of motion are three physical laws that form the basis for classical mechanics. They describe the relationship between the forces acting on a body and its motion due to those forces...
in an inertial frame of reference
Inertial frame of reference
In physics, an inertial frame of reference is a frame of reference that describes time homogeneously and space homogeneously, isotropically, and in a time-independent manner.All inertial frames are in a state of constant, rectilinear motion with respect to one another; they are not...
: in an inertial frame, the motion of an object is explained by the real impressed forces. In a non-inertial frame such as a rotating frame, however, Newton's first and second laws still can be used to make accurate physical predictions provided fictitious forces are included along with the real forces. For solving problems of mechanics in non-inertial reference frames, the advice given in textbooks is to treat the fictitious forces like real forces and to pretend you are in an inertial frame.
It should be mentioned that "treating the fictitious forces like real forces" means, in particular, that fictitious forces as seen in a particular non-inertial frame transform as vectors under coordinate transformations made within that frame, that is, like real forces.
Moving objects and observational frames of reference
Next, it is observed that time varying coordinates are used in both inertial and non-inertial frames of reference, so the use of time varying coordinates should not be confounded with a change of observer, but is only a change of the observer's choice of description. Elaboration of this point and some citations on the subject follow.Frame of reference and coordinate system
The term frame of referenceFrame of reference
A frame of reference in physics, may refer to a coordinate system or set of axes within which to measure the position, orientation, and other properties of objects in it, or it may refer to an observational reference frame tied to the state of motion of an observer.It may also refer to both an...
is used often in a very broad sense, but for the present discussion its meaning is restricted to refer to an observer's state of motion, that is, to either an inertial frame of reference or a non-inertial frame of reference.
The term coordinate system
Coordinate system
In geometry, a coordinate system is a system which uses one or more numbers, or coordinates, to uniquely determine the position of a point or other geometric element. The order of the coordinates is significant and they are sometimes identified by their position in an ordered tuple and sometimes by...
is used to differentiate between different possible choices for a set of variables to describe motion, choices available to any observer, regardless of their state of motion. Examples are Cartesian coordinates, polar coordinates and (more generally) curvilinear coordinates
Curvilinear coordinates
Curvilinear coordinates are a coordinate system for Euclidean space in which the coordinate lines may be curved. These coordinates may be derived from a set of Cartesian coordinates by using a transformation that is locally invertible at each point. This means that one can convert a point given...
.
Here are two quotes relating "state of motion" and "coordinate system":
Time varying coordinate systems
In a general coordinate system, the basis vectors for the coordinates may vary in time at fixed positions, or they may vary with position at fixed times, or both. It may be noted that coordinate systems attached to both inertial frames and non-inertial frames can have basis vectors that vary in time, space or both, for example the description of a trajectory in polar coordinates as seen from an inertial frame. or as seen from a rotating frame. A time-dependent description of observations does not change the frame of reference in which the observations are made and recorded.Fictitious forces in a local coordinate system
In discussion of a particle moving in a circular orbit, in an inertial frame of reference one can identify the centripetal and tangential forces. It then seems to be no problem to switch hats, change perspective, and talk about the fictitious forces commonly called the centrifugal and Euler force
Euler force
In classical mechanics, the Euler acceleration , also known as azimuthal acceleration or transverse acceleration is an acceleration that appears when a non-uniformly rotating reference frame is used for analysis of motion and there is variation in the angular velocity of the reference frame's axes...
. But what underlies this switch in vocabulary is a change of observational frame of reference from the inertial frame where we started, where centripetal and tangential forces make sense, to a rotating frame of reference where the particle appears motionless and fictitious centrifugal and Euler forces have to be brought into play. That switch is unconscious, but real.
Suppose we sit on a particle in general planar motion (not just a circular orbit). What analysis underlies a switch of hats to introduce fictitious centrifugal and Euler forces?
To explore that question, begin in an inertial frame of reference. By using a coordinate system commonly used in planar motion, the so-called local coordinate system, as shown in Figure 1, it becomes easy to identify formulas for the centripetal inward force normal to the trajectory (in direction opposite to un in Figure 1), and the tangential force parallel to the trajectory (in direction ut), as shown next.
To introduce the unit vectors of the local coordinate system shown in Figure 1, one approach is to begin in Cartesian coordinates in an inertial framework and describe the local coordinates in terms of these Cartesian coordinates. In Figure 1, the arc length
Arc length
Determining the length of an irregular arc segment is also called rectification of a curve. Historically, many methods were used for specific curves...
s is the distance the particle has traveled along its path in time t. The path r (t) with components x(t), y(t) in Cartesian coordinates is described using arc length s(t) as:
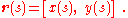
One way to look at the use of s is to think of the path of the particle as sitting in space, like the trail left by a skywriter
Skywriting
Skywriting is the process of using a small aircraft, able to expel special smoke during flight, to fly in certain patterns to create writing readable by someone on the ground...
, independent of time. Any position on this path is described by stating its distance s from some starting point on the path. Then an incremental displacement along the path ds is described by:
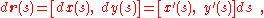
where primes are introduced to denote derivatives with respect to s. The magnitude of this displacement is ds, showing that:
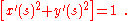(Eq. 1)This displacement is necessarily tangent to the curve at s, showing that the unit vector tangent to the curve is:
while the outward unit vector normal to the curve is
Orthogonality can be verified by showing the vector dot product
Dot product
In mathematics, the dot product or scalar product is an algebraic operation that takes two equal-length sequences of numbers and returns a single number obtained by multiplying corresponding entries and then summing those products...
is zero. The unit magnitude of these vectors is a consequence of Eq. 1.
As an aside, notice that the use of unit vectors that are not aligned along the Cartesian xy-axes does not mean we are no longer in an inertial frame. All it means is that we are using unit vectors that vary with s to describe the path, but still observe the motion from the inertial frame.
Using the tangent vector, the angle of the tangent to the curve, say θ, is given by:
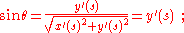and The radius of curvature is introduced completely formally (without need for geometric interpretation) as:
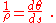
The derivative of θ can be found from that for sin θ:
Now:
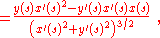
in which the denominator is unity according to Eq. 1. With this formula for the derivative of the sine, the radius of curvature becomes:
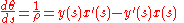
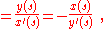
where the equivalence of the forms stems from differentiation of Eq. 1:
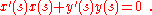
Having set up the description of any position on the path in terms of its associated value for s, and having found the properties of the path in terms of this description, motion of the particle is introduced by stating the particle position at any time t as the corresponding value s (t).
Using the above results for the path properties in terms of s, the acceleration in the inertial reference frame as described in terms of the components normal and tangential to the path of the particle can be found in terms of the function s(t) and its various time derivatives (as before, primes indicate differentiation with respect to s):
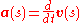
as can be verified by taking the dot product with the unit vectors ut(s) and un(s). This result for acceleration is the same as that for circular motion based on the radius ρ. Using this coordinate system in the inertial frame, it is easy to identify the force normal to the trajectory as the centripetal force and that parallel to the trajectory as the tangential force.
Next, we change observational frames. Sitting on the particle, we adopt a non-inertial frame where the particle is at rest (zero velocity). This frame has a continuously changing origin, which at time t is the center of curvature (the center of the osculating circle
Osculating circle
In differential geometry of curves, the osculating circle of a sufficiently smooth plane curve at a given point p on the curve has been traditionally defined as the circle passing through p and a pair of additional points on the curve infinitesimally close to p...
in Figure 1) of the path at time t, and whose rate of rotation is the angular rate of motion of the particle about that origin at time t. This non-inertial frame also employs unit vectors normal to the trajectory and parallel to it.
The angular velocity
Angular velocity
In physics, the angular velocity is a vector quantity which specifies the angular speed of an object and the axis about which the object is rotating. The SI unit of angular velocity is radians per second, although it may be measured in other units such as degrees per second, revolutions per...
of this frame is the angular velocity of the particle about the center of curvature at time t. The centripetal force of the inertial frame is interpreted in the non-inertial frame where the body is at rest as a force necessary to overcome the centrifugal force. Likewise, the force causing any acceleration of speed along the path seen in the inertial frame becomes the force necessary to overcome the Euler force in the non-inertial frame where the particle is at rest. There is zero Coriolis force in the frame, because the particle has zero velocity in this frame. For a pilot in an airplane, for example, these fictitious forces are a matter of direct experience. However, these fictitious forces cannot be related to a simple observational frame of reference other than the particle itself, unless it is in a particularly simple path, like a circle.
That said, from a qualitative standpoint, the path of an airplane can be approximated by an arc of a circle for a limited time, and for the limited time a particular radius of curvature applies, the centrifugal and Euler forces can be analyzed on the basis of circular motion with that radius. See article discussing turning an airplane.
Next, reference frames rotating about a fixed axis are discussed in more detail.
Fictitious forces in polar coordinates
Description of particle motion often is simpler in non-Cartesian coordinate systems, for example, polar coordinates. When equations of motion are expressed in terms of any curvilinear coordinate system, extra terms appear that represent how the basis vectors change as the coordinates change. These terms arise automatically on transformation to polar (or cylindrical) coordinates and are thus not fictitious forces, but rather are simply added terms in the acceleration in polar coordinates.Two terminologies
In a purely mathematical treatment, regardless of the frame that the coordinate system is associated with (inertial or non-inertial), extra terms appear in the acceleration of an observed particle when using curvilinear coordinates. For example, in polar coordinates the acceleration is given by (see below for details):
which contains not just double time derivatives of the coordinates but added terms. This example employs polar coordinates, but more generally the added terms depend upon which coordinate system is chosen (that is, polar, elliptic, or whatever).
Sometimes these coordinate-system dependent terms also are referred to as "fictitious forces", introducing a second meaning for "fictitious forces", despite the fact that these terms do not have the vector transformation properties
General covariance
In theoretical physics, general covariance is the invariance of the form of physical laws under arbitrary differentiable coordinate transformations...
expected of forces. For example, see Shankar and Hildebrand. According to this terminology, fictitious forces are determined in part by the coordinate system itself, regardless of the frame it is attached to, that is, regardless of whether the coordinate system is attached to an inertial or a non-inertial frame of reference. In contrast, the fictitious forces defined in terms of the state of motion of the observer vanish in inertial frames of reference. To distinguish these two terminologies, the fictitious forces that vanish in an inertial frame of reference, the inertial forces of Newtonian mechanics, are called in this article the "state-of-motion" fictitious forces and those that originate in the interpretation of time derivatives in particular coordinate systems are called "coordinate" fictitious forces.
Assuming it is clear that "state of motion" and "coordinate system" are different, it follows that the dependence of centrifugal force (as in this article) upon "state of motion" and its independence from "coordinate system", which contrasts with the "coordinate" version with exactly the opposite dependencies, indicates that two different ideas are referred to by the terminology "fictitious force". The present article emphasizes one of these two ideas ("state-of-motion"), although the other also is described.
Below, polar coordinates are introduced for use in (first) an inertial frame of reference and then (second) in a rotating frame of reference. The two different uses of the term "fictitious force" are pointed out. First, however, follows a brief digression to explain further how the "coordinate" terminology for fictitious force has arisen.
Lagrangian approach
To motivate the introduction of "coordinate" inertial forces by more than a reference to "mathematical convenience", what follows is a digression to show these forces correspond to what are called by some authors "generalized" fictitious forces or "generalized inertia forces". These forces are introduced via the Lagrangian mechanicsLagrangian mechanics
Lagrangian mechanics is a re-formulation of classical mechanics that combines conservation of momentum with conservation of energy. It was introduced by the Italian-French mathematician Joseph-Louis Lagrange in 1788....
approach to mechanics based upon describing a system by generalized coordinates usually denoted as {qk}. The only requirement on these coordinates is that they are necessary and sufficient to uniquely characterize the state of the system: they need not be (although they could be) the coordinates of the particles in the system. Instead, they could be the angles and extensions of links in a robot arm, for instance. If a mechanical system consists of N particles and there are m independent kinematical conditions imposed, it is possible to characterize the system uniquely by n = 3N - m independent generalized coordinates
Generalized coordinates
In the study of multibody systems, generalized coordinates are a set of coordinates used to describe the configuration of a system relative to some reference configuration....
{qk}.
In classical mechanics, the Lagrangian is defined as the kinetic energy
Kinetic energy
The kinetic energy of an object is the energy which it possesses due to its motion.It is defined as the work needed to accelerate a body of a given mass from rest to its stated velocity. Having gained this energy during its acceleration, the body maintains this kinetic energy unless its speed changes...
,
, of the system minus its potential energyPotential energy
In physics, potential energy is the energy stored in a body or in a system due to its position in a force field or due to its configuration. The SI unit of measure for energy and work is the Joule...
,
. In symbols,Under conditions that are given in Lagrangian mechanics
Lagrangian mechanics
Lagrangian mechanics is a re-formulation of classical mechanics that combines conservation of momentum with conservation of energy. It was introduced by the Italian-French mathematician Joseph-Louis Lagrange in 1788....
, if the Lagrangian of a system is known, then the equations of motion
Equation of motion
Equations of motion are equations that describe the behavior of a system in terms of its motion as a function of time...
of the system may be obtained by a direct substitution of the expression for the Lagrangian into the Euler–Lagrange equation, a particular family of partial differential equation
Partial differential equation
In mathematics, partial differential equations are a type of differential equation, i.e., a relation involving an unknown function of several independent variables and their partial derivatives with respect to those variables...
s.
Here are some definitions:
- Definition:
- is the Lagrange function or Lagrangian, qi are the generalized coordinates,
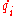are generalized velocities,
are generalized momenta,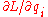
are generalized forces,
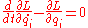are Lagrange's equations.
It is not the purpose here to outline how Lagrangian mechanics works. The interested reader can look at other articles explaining this approach. For the moment, the goal is simply to show that the Lagrangian approach can lead to "generalized fictitious forces" that do not vanish in inertial frames. What is pertinent here is that in the case of a single particle, the Lagrangian approach can be arranged to capture exactly the "coordinate" fictitious forces just introduced.
To proceed, consider a single particle, and introduce the generalized coordinates as {qk} = (r, θ). Then Hildebrand shows in polar coordinates with the qk = (r, θ) the "generalized momenta" are:
leading, for example, to the generalized force:
with Qr the impressed radial force. The connection between "generalized forces" and Newtonian forces varies with the choice of coordinates. This Lagrangian formulation introduces exactly the "coordinate" form of fictitious forces mentioned above that allows "fictitious" (generalized) forces in inertial frames, for example, the term
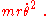Careful reading of Hildebrand shows he doesn't discuss the role of "inertial frames of reference", and in fact, says "[The] presence or absence [of inertia forces] depends, not upon the particular problem at hand but upon the coordinate system chosen." By coordinate system presumably is meant the choice of {qk}. Later he says "If accelerations associated with generalized coordinates are to be of prime interest (as is usually the case), the [nonaccelerational] terms may be conveniently transferred to the right … and considered as additional (generalized) inertia forces. Such inertia forces are often said to be of the Coriolis type."In short, the emphasis of some authors upon coordinates and their derivatives and their introduction of (generalized) fictitious forces that do not vanish in inertial frames of reference is an outgrowth of the use of generalized coordinates
Generalized coordinates
In the study of multibody systems, generalized coordinates are a set of coordinates used to describe the configuration of a system relative to some reference configuration....
in Lagrangian mechanics
Lagrangian mechanics
Lagrangian mechanics is a re-formulation of classical mechanics that combines conservation of momentum with conservation of energy. It was introduced by the Italian-French mathematician Joseph-Louis Lagrange in 1788....
. For example, see McQuarrie Hildebrand, and von Schwerin. Below is an example of this usage as employed in the design of robotic manipulators:
For a robot manipulator, the equations may be written in a form using Christoffel symbols
Christoffel symbols
In mathematics and physics, the Christoffel symbols, named for Elwin Bruno Christoffel , are numerical arrays of real numbers that describe, in coordinates, the effects of parallel transport in curved surfaces and, more generally, manifolds. As such, they are coordinate-space expressions for the...
Γijk (discussed further below) as:
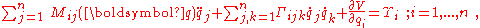
where M is the "manipulator inertia matrix" and V is the potential energy due to gravity (for example), and
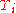are the generalized forces on joint i. The terms involving Christoffel symbols therefore determine the "generalized centrifugal" and "generalized Coriolis" terms.The introduction of generalized fictitious forces often is done without notification and without specifying the word "generalized". This sloppy use of terminology leads to endless confusion because these generalized fictitious forces, unlike the standard "state-of-motion" fictitious forces, do not vanish in inertial frames of reference.
Polar coordinates in an inertial frame of reference
Below, the acceleration of a particle is derived as seen in an inertial frame using polar coordinates. There are no "state-of-motion" fictitious forces in an inertial frame, by definition. Following that presentation, the contrasting terminology of "coordinate" fictitious forces is presented and critiqued on the basis of the non-vectorial transformation behavior of these "forces".In an inertial frame, let
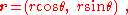
be the position vector of a moving particle. Its Cartesian components (x, y) are:with polar coordinates r and θ depending on time t.
Unit vectors are defined in the radially outward direction
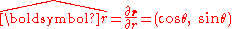
:and in the direction at right angles to
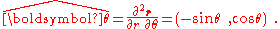
: These unit vectors vary in direction with time:
and:
Using these derivatives, the first and second derivatives of position are:
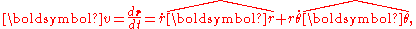
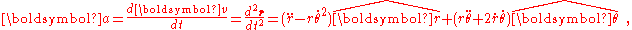
where dot-overmarkings indicate time differentiation. With this form for the acceleration
, in an inertial frame of reference Newton's second law expressed in polar coordinates is: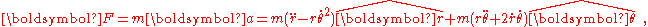where F is the net real force on the particle. No fictitious forces appear because all fictitious forces are zero by definition in an inertial frame.
From a mathematical standpoint, however, it sometimes is handy to put only the second-order derivatives on the right side of this equation; that is we write the above equation by rearrangement of terms as:
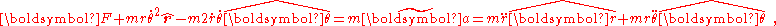
where a "coordinate" version of the "acceleration" is introduced:
consisting of only second-order time derivatives of the coordinates r and θ. The terms moved to the force-side of the equation are now treated as extra "fictitious forces" and, confusingly, the resulting forces also are called the "centrifugal" and "Coriolis" force.
These newly defined "forces" are non-zero in an inertial frame, and so certainly are not the same as the previously identified fictitious forces that are zero in an inertial frame and non-zero only in a non-inertial frame. In this article, these newly defined forces are called the "coordinate" centrifugal force and the "coordinate" Coriolis force to separate them from the "state-of-motion" forces.
Change of origin
Here is an illustration showing the so called "centrifugal term" does not transform as a true force, putting any reference to this term not just as a "term", but as a centrifugal force, in a dubious light. Suppose in frame S a particle moves radially away from the origin at a constant velocity. See Figure 2. The force on the particle is zero by Newton's first law. Now we look at the same thing from frame S' , which is the same, but displaced in origin. In S' the particle still is in straight line motion at constant speed, so again the force is zero.What if we use polar coordinates in the two frames? In frame S the radial motion is constant and there is no angular motion. Hence, the acceleration is:
and each term individually is zero because
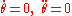and . There is no force, including no 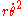"force" in frame S.In frame S' , however, we have:
In this case the azimuthal term is zero, being the rate of change of angular momentum. To obtain zero acceleration in the radial direction, however, we require:
The right-hand side is non-zero, inasmuch as neither
nor 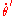is zero. That is, we cannot obtain zero force (zero ) if we retain only 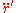as the acceleration; we need both terms.Despite the above facts, suppose we adopt polar coordinates, and wish to say that
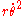is "centrifugal force", and reinterpret 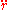as "acceleration" (without dwelling upon any possible justification). How does this decision fare when we consider that a proper formulation of physics is geometry and coordinate-independent? See the article on general covarianceGeneral covariance
In theoretical physics, general covariance is the invariance of the form of physical laws under arbitrary differentiable coordinate transformations...
. To attempt to form a covariant expression, this so-called centrifugal "force" can be put into vector notation as:
with:
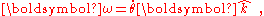
and
a unit vector normal to the plane of motion. Unfortunately, although this expression formally looks like a vector, when an observer changes origin the value of changes (see Figure 2), so observers in the same frame of reference standing on different street corners see different "forces" even though the actual events they witness are identical.How can a physical force (be it fictitious or real) be zero in one frame S, but non-zero in another frame S' identical, but a few feet away? Even for exactly the same particle behavior the expression
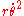is different in every frame of reference, even for very trivial distinctions between frames. In short, if we take as "centrifugal force", it does not have a universal significance: it is unphysical.Beyond this problem, the real impressed net force is zero. (There is no real impressed force in straight-line motion at constant speed). If we adopt polar coordinates, and wish to say that
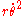is "centrifugal force", and reinterpret 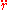as "acceleration", the oddity results in frame S' that straight-line motion at constant speed requires a net force in polar coordinates, but not in Cartesian coordinates. Moreover, this perplexity applies in frame S, but not in frame S.The absurdity of the behavior of
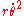indicates that one must say that 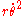is not centrifugal force, but simply one of two terms in the acceleration. This view, that the acceleration is composed of two terms, is frame-independent: there is zero centrifugal force in any and every inertial frame. It also is coordinate-system independent: we can use Cartesian, polar, or any other curvilinear system: they all produce zero.Apart from the above physical arguments, of course, the derivation above, based upon application of the mathematical rules of differentiation, shows the radial acceleration does indeed consist of the two terms
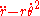.That said, the next subsection shows there is a connection between these centrifugal and Coriolis terms and the fictitious forces that pertain to a particular rotating frame of reference (as distinct from an inertial frame).
Co-rotating frame
In the case of planar motion of a particle, the "coordinate" centrifugal and Coriolis acceleration terms found above to be non-zero in an inertial frame can be shown to be the negatives of the "state-of-motion" centrifugal and Coriolis terms that appear in a very particular non-inertial co-rotating frame (see next subsection). See Figure 3. To define a co-rotating frame, first an origin is selected from which the distance r(t) to the particle is defined. An axis of rotation is set up that is perpendicular to the plane of motion of the particle, and passing through this origin. Then, at the selected moment t, the rate of rotation of the co-rotating frame Ω is made to match the rate of rotation of the particle about this axis, dθ/dt. The co-rotating frame applies only for a moment, and must be continuously re-selected as the particle moves. For more detail, see Polar coordinates, centrifugal and Coriolis terms.Polar coordinates in a rotating frame of reference
Next, the same approach is used to find the fictitious forces of a (non-inertial) rotating frame. For example, if a rotating polar coordinate system is adopted for use in a rotating frame of observation, both rotating at the same constant counterclockwise rate Ω, we find the equations of motion in this frame as follows: the radial coordinate in the rotating frame is taken as r, but the angle θ' in the rotating frame changes with time:Consequently,
Plugging this result into the acceleration using the unit vectors of the previous section:
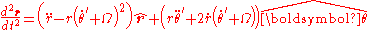
The leading two terms are the same form as those in the inertial frame, and they are the only terms if the frame is not rotating, that is, if Ω=0. However, in this rotating frame we have the extra terms:
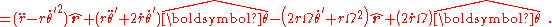
The radial term Ω2 r is the centrifugal force per unit mass due to the system's rotation at rate Ω and the radial term
is the radial component of the Coriolis force per unit mass, where is the tangential component of the particle velocity as seen in the rotating frame. The term is the so-called azimuthal component of the Coriolis force per unit mass. In fact, these extra terms can be used to measure Ω and provide a test to see whether or not the frame is rotating, just as explained in the example of rotating identical spheresRotating spheres
Isaac Newton's rotating spheres argument attempts to demonstrate that true rotational motion can be defined by observing the tension in the string joining two identical spheres...
. If the particle's motion can be described by the observer using Newton's laws of motion without these Ω-dependent terms, the observer is in an inertial frame of reference
Inertial frame of reference
In physics, an inertial frame of reference is a frame of reference that describes time homogeneously and space homogeneously, isotropically, and in a time-independent manner.All inertial frames are in a state of constant, rectilinear motion with respect to one another; they are not...
where Ω=0.
These "extra terms" in the acceleration of the particle are the "state of motion" fictitious forces for this rotating frame, the forces introduced by rotation of the frame at angular rate Ω.
In this rotating frame, what are the "coordinate" fictitious forces? As before, suppose we choose to put only the second-order time derivatives on the right side of Newton's law:
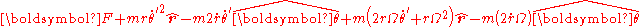
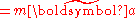
If we choose for convenience to treat
as some so-called "acceleration", then the terms 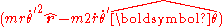are added to the so-called "fictitious force", which are not "state-of-motion" fictitious forces, but are actually components of force that persist even when Ω=0, that is, they persist even in an inertial frame of reference. Because these extra terms are added, the "coordinate" fictitious force is not the same as the "state-of-motion" fictitious force. Because of these extra terms, the "coordinate" fictitious force is not zero even in an inertial frame of reference.More on the co-rotating frame
Notice however, the case of a rotating frame that happens to have the same angular rate as the particle, so that Ω = dθ/dt at some particular moment (that is, the polar coordinates are set up in the instantaneous, non-inertial co-rotating frame of Figure 3). In this case, at this moment, dθ'/dt = 0. In this co-rotating non-inertial frame at this moment the "coordinate" fictitious forces are only those due to the motion of the frame, that is, they are the same as the "state-of-motion" fictitious forces, as discussed in the remarks about the co-rotating frame of Figure 3 in the previous section.Fictitious forces in curvilinear coordinates
Differentiable manifold
A differentiable manifold is a type of manifold that is locally similar enough to a linear space to allow one to do calculus. Any manifold can be described by a collection of charts, also known as an atlas. One may then apply ideas from calculus while working within the individual charts, since...
."
Instead of Cartesian coordinates, when equations of motion are expressed in a curvilinear coordinate
Curvilinear coordinates
Curvilinear coordinates are a coordinate system for Euclidean space in which the coordinate lines may be curved. These coordinates may be derived from a set of Cartesian coordinates by using a transformation that is locally invertible at each point. This means that one can convert a point given...
system, Christoffel symbols appear in the acceleration of a particle expressed in this coordinate system, as described below in more detail. Consider description of a particle motion from the viewpoint of an inertial frame of reference in curvilinear coordinates. Suppose the position of a point P in Cartesian coordinates is (x, y, z) and in curvilinear coordinates is (q1, q2. q3). Then functions exist that relate these descriptions:
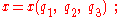
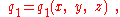
and so forth. (The number of dimensions may be larger than three.) An important aspect of such coordinate systems is the element of arc length that allows distances to be determined. If the curvilinear coordinates form an orthogonal coordinate
Orthogonal coordinates
In mathematics, orthogonal coordinates are defined as a set of d coordinates q = in which the coordinate surfaces all meet at right angles . A coordinate surface for a particular coordinate qk is the curve, surface, or hypersurface on which qk is a constant...
system, the element of arc length ds is expressed as:
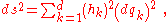
where the quantities hk are called scale factors. A change dqk in qk causes a displacement hk dqk along the coordinate line for qk. At a point P, we place unit vectors ek each tangent to a coordinate line of a variable qk. Then any vector can be expressed in terms of these basis vectors, for example, from an inertial frame of reference, the position vector of a moving particle r located at time t at position P becomes:
where qk is the vector dot product
Dot product
In mathematics, the dot product or scalar product is an algebraic operation that takes two equal-length sequences of numbers and returns a single number obtained by multiplying corresponding entries and then summing those products...
of r and ek.
The velocity v of a particle at P, can be expressed at P as:
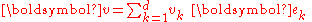
where vk is the vector dot product
Dot product
In mathematics, the dot product or scalar product is an algebraic operation that takes two equal-length sequences of numbers and returns a single number obtained by multiplying corresponding entries and then summing those products...
of v and ek, and over dots indicate time differentiation.
The time derivatives of the basis vectors can be expressed in terms of the scale factors introduced above. for example:
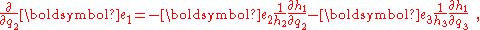or, in general,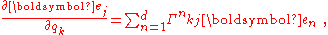 in which the coefficients of the unit vectors are the Christoffel symbols
Christoffel symbols
In mathematics and physics, the Christoffel symbols, named for Elwin Bruno Christoffel , are numerical arrays of real numbers that describe, in coordinates, the effects of parallel transport in curved surfaces and, more generally, manifolds. As such, they are coordinate-space expressions for the...
for the coordinate system. The general notation and formulas for the Christoffel symbols are:
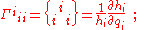
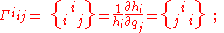
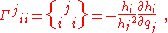
and the symbol is zero when all the indices are different. Despite appearances to the contrary, the Christoffel symbols do not form the components of a tensor. For example, they are zero in Cartesian coordinates, but not in polar coordinates.
Using relations like this one,
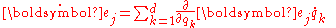
which allows all the time derivatives to be evaluated. For example, for the velocity:
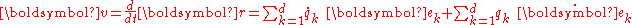
with the Γ-notation for the Christoffel symbols replacing the curly bracket notation.
Using the same approach, the acceleration is then
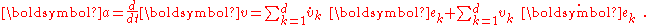
Looking at the relation for acceleration, the first summation contains the time derivatives of velocity, which would be associated with acceleration if these were Cartesian coordinates, and the second summation (the one with Christoffel symbols) contains terms related to the way the unit vectors change with time.
"State-of-motion" versus "coordinate" fictitious forces
Earlier in this article a distinction was introduced between two terminologies, the fictitious forces that vanish in an inertial frame of reference are called in this article the "state-of-motion" fictitious forces and those that originate from differentiation in a particular coordinate system are called "coordinate" fictitious forces. Using the expression for the acceleration above, Newton's law of motion in the inertial frame of reference becomes: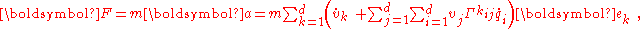where F is the net real force on the particle. No "state-of-motion" fictitious forces are present because the frame is inertial, and "state-of-motion" fictitious forces are zero in an inertial frame, by definition.
The "coordinate" approach to Newton's law above is to retain the second-order time derivatives of the coordinates {qk} as the only terms on the right side of this equation, motivated more by mathematical convenience than by physics. To that end, the force law can be rewritten, taking the second summation to the force-side of the equation as:
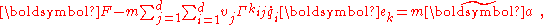
with the convention that the "acceleration"
is now:In the expression above, the summation added to the force-side of the equation now is treated as if added "forces" were present. These summation terms are customarily called fictitious forces within this "coordinate" approach, although in this inertial frame of reference all "state-of-motion" fictitious forces are identically zero. Moreover, these "forces" do not transform under coordinate transformations as vectors. Thus, the designation of the terms of the summation as "fictitious forces" uses this terminology for contributions that are completely different from any real force, and from the "state-of-motion" fictitious forces. What adds to this confusion is that these "coordinate" fictitious forces are divided into two groups and given the same names as the "state-of-motion" fictitious forces, that is, they are divided into "centrifugal" and "Coriolis" terms, despite their inclusion of terms that are not the "state-of-motion" centrifugal and Coriolis terms. For example, these "coordinate" centrifugal and Coriolis terms can be nonzero even in an inertial frame of reference where the "state-of-motion" centrifugal force (the subject of this article) and Coriolis force always are zero.
If the frame is not inertial, for example, in a rotating frame of reference, the "state-of-motion" fictitious forces are included in the above "coordinate" fictitious force expression. Also, if the "acceleration" expressed in terms of first-order time derivatives of the velocity happens to result in terms that are not simply second-order derivatives of the coordinates {qk} in time, then these terms that are not second-order also are brought to the force-side of the equation and included with the fictitious forces. From the standpoint of a Lagrangian formulation, they can be called generalized fictitious forces. See Hildebrand , for example.
Formulation of dynamics in terms of Christoffel symbols and the "coordinate" version of fictitious forces is used often in the design of robots
Robotics
Robotics is the branch of technology that deals with the design, construction, operation, structural disposition, manufacture and application of robots...
in connection with a Lagrangian formulation
Lagrangian mechanics
Lagrangian mechanics is a re-formulation of classical mechanics that combines conservation of momentum with conservation of energy. It was introduced by the Italian-French mathematician Joseph-Louis Lagrange in 1788....
of the equations of motion.
Further reading
- Newton's description in Principia
- Centrifugal reaction force - Columbia electronic encyclopedia
- M. Alonso and E.J. Finn, Fundamental university physics, Addison-Wesley
- Centripetal force vs. Centrifugal force - from an online Regents Exam physics tutorial by the Oswego City School District
- Centrifugal force acts inwards near a black hole
- Centrifugal force at the HyperPhysics concepts site
- A list of interesting links
External links
- Motion over a flat surface Java physlet by Brian Fiedler (from School of Meteorology at the University of Oklahoma) illustrating fictitious forces. The physlet shows both the perspective as seen from a rotating and from a non-rotating point of view.
- Motion over a parabolic surface Java physlet by Brian Fiedler (from School of Meteorology at the University of Oklahoma) illustrating fictitious forces. The physlet shows both the perspective as seen from a rotating and as seen from a non-rotating point of view.
- Animation clip showing scenes as viewed from both an inertial frame and a rotating frame of reference, visualizing the Coriolis and centrifugal forces.
- Centripetal and Centrifugal Forces at MathPages
- Centrifugal Force at h2g2
- John Baez: Does centrifugal force hold the Moon up?
See also
- Calculating relative centrifugal force
- Circular motionCircular motionIn physics, circular motion is rotation along a circular path or a circular orbit. It can be uniform, that is, with constant angular rate of rotation , or non-uniform, that is, with a changing rate of rotation. The rotation around a fixed axis of a three-dimensional body involves circular motion of...
- Coriolis forceCoriolis effectIn physics, the Coriolis effect is a deflection of moving objects when they are viewed in a rotating reference frame. In a reference frame with clockwise rotation, the deflection is to the left of the motion of the object; in one with counter-clockwise rotation, the deflection is to the right...
- Coriolis effect (perception)Coriolis effect (perception)In psychophysical perception, the Coriolis effect is the misperception of body orientation and induced nausea due to the Coriolis force ....
- Centripetal forceCentripetal forceCentripetal force is a force that makes a body follow a curved path: it is always directed orthogonal to the velocity of the body, toward the instantaneous center of curvature of the path. The mathematical description was derived in 1659 by Dutch physicist Christiaan Huygens...
- Equivalence principleEquivalence principleIn the physics of general relativity, the equivalence principle is any of several related concepts dealing with the equivalence of gravitational and inertial mass, and to Albert Einstein's assertion that the gravitational "force" as experienced locally while standing on a massive body is actually...
- Bucket argumentBucket argumentIsaac Newton's rotating bucket argument was designed to demonstrate that true rotational motion cannot be defined as the relative rotation of the body with respect to the immediately surrounding bodies...
- Frame of referenceFrame of referenceA frame of reference in physics, may refer to a coordinate system or set of axes within which to measure the position, orientation, and other properties of objects in it, or it may refer to an observational reference frame tied to the state of motion of an observer.It may also refer to both an...
- Inertial frame of referenceInertial frame of referenceIn physics, an inertial frame of reference is a frame of reference that describes time homogeneously and space homogeneously, isotropically, and in a time-independent manner.All inertial frames are in a state of constant, rectilinear motion with respect to one another; they are not...
- Rotational motion
- Euler forceEuler forceIn classical mechanics, the Euler acceleration , also known as azimuthal acceleration or transverse acceleration is an acceleration that appears when a non-uniformly rotating reference frame is used for analysis of motion and there is variation in the angular velocity of the reference frame's axes...
- a force that appears when the frame angular rotation rate varies - Reactive centrifugal forceReactive centrifugal forceIn classical mechanics, reactive centrifugal force is the reaction paired with centripetal force. A mass undergoing circular motion constantly accelerates toward the axis of rotation. This centripetal acceleration is caused by a force exerted on the mass by some other object. In accordance with...
- a force that occurs as reaction due to a centripetal force - Fictitious forceFictitious forceA fictitious force, also called a pseudo force, d'Alembert force or inertial force, is an apparent force that acts on all masses in a non-inertial frame of reference, such as a rotating reference frame....
– a force that can be made to vanish by changing frame of reference - Orthogonal coordinatesOrthogonal coordinatesIn mathematics, orthogonal coordinates are defined as a set of d coordinates q = in which the coordinate surfaces all meet at right angles . A coordinate surface for a particular coordinate qk is the curve, surface, or hypersurface on which qk is a constant...
- Osculating circleOsculating circleIn differential geometry of curves, the osculating circle of a sufficiently smooth plane curve at a given point p on the curve has been traditionally defined as the circle passing through p and a pair of additional points on the curve infinitesimally close to p...
- Frenet-Serret formulasFrenet-Serret formulasIn vector calculus, the Frenet–Serret formulas describe the kinematic properties of a particle which moves along a continuous, differentiable curve in three-dimensional Euclidean space R3...
- StaticsStaticsStatics is the branch of mechanics concerned with the analysis of loads on physical systems in static equilibrium, that is, in a state where the relative positions of subsystems do not vary over time, or where components and structures are at a constant velocity...
- Kinetics (physics)Kinetics (physics)In physics and engineering, kinetics is a term for the branch of classical mechanics that is concerned with the relationship between the motion of bodies and its causes, namely forces and torques...
- KinematicsKinematicsKinematics is the branch of classical mechanics that describes the motion of bodies and systems without consideration of the forces that cause the motion....
- Applied mechanicsApplied mechanicsApplied mechanics is a branch of the physical sciences and the practical application of mechanics. Applied mechanics examines the response of bodies or systems of bodies to external forces...
- Analytical mechanicsAnalytical mechanicsAnalytical mechanics is a term used for a refined, mathematical form of classical mechanics, constructed from the 18th century onwards as a formulation of the subject as founded by Isaac Newton. Often the term vectorial mechanics is applied to the form based on Newton's work, to contrast it with...
- Dynamics (physics)
- Classical mechanicsClassical mechanicsIn physics, classical mechanics is one of the two major sub-fields of mechanics, which is concerned with the set of physical laws describing the motion of bodies under the action of a system of forces...
- D'Alembert's principleD'Alembert's principleD'Alembert's principle, also known as the Lagrange–d'Alembert principle, is a statement of the fundamental classical laws of motion. It is named after its discoverer, the French physicist and mathematician Jean le Rond d'Alembert...
- CentrifugeCentrifugeA centrifuge is a piece of equipment, generally driven by an electric motor , that puts an object in rotation around a fixed axis, applying a force perpendicular to the axis...