
Equation of motion
Encyclopedia
Equations of motion are equations that describe the behavior of a system in terms of its motion
as a function of time (e.g., the motion of a particle under the influence of a force
). Sometimes the term refers to the differential equations that the system satisfies (e.g., Newton's second law or Euler–Lagrange equations), and sometimes to the solutions to those equations.
are often referred to as "SUVAT" equations where the five variables are represented by those letters (s = displacement, u = initial velocity, v = final velocity, a = acceleration, t = time); the five letters may be shown in a different order.
The body is considered between two instants in time: one initial point and one current (or final) point. Problems in kinematics may deal with more than two instants, and several applications of the equations are then required. If a is constant, the differential, a dt, may be integrated over an interval from 0 to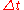 (
( ), to obtain a linear relationship for velocity. Integration of the velocity yields a quadratic relationship for position at the end of the interval.
), to obtain a linear relationship for velocity. Integration of the velocity yields a quadratic relationship for position at the end of the interval.
Note that each of the equations contains four of the five variables.
Thus, in this situation it is sufficient to know three out of the five variables to calculate the remaining two.

By substituting (1) into (2), we can get (3), (4) and (5). (6) can be constructed by rearranging (1).
where
s, for example a ball thrown upwards into the air.
Given initial speed u, one can calculate how high the ball will travel before it begins to fall.
The acceleration is local acceleration of gravity g. At this point one must remember that while these quantities appear to be scalars
, the direction of displacement, speed and acceleration is important. They could in fact be considered as uni-directional vectors. Choosing s to measure up from the ground, the acceleration a must be in fact −g, since the force of gravity acts downwards and therefore also the acceleration on the ball due to it.
At the highest point, the ball will be at rest: therefore v = 0. Using the fifth equation, we have:
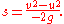
Substituting and cancelling minus signs gives:
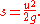

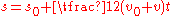

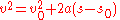
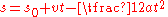
:

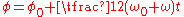
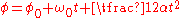
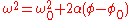
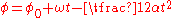
where: is the angular acceleration
is the angular acceleration
 is the angular velocity
is the angular velocity
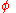 is the angular displacement
is the angular displacement
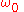 is the initial angular velocity.
is the initial angular velocity.

Hence: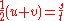
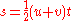
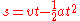
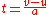
Using equation 2, substitute t with above: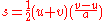


Motion (physics)
In physics, motion is a change in position of an object with respect to time. Change in action is the result of an unbalanced force. Motion is typically described in terms of velocity, acceleration, displacement and time . An object's velocity cannot change unless it is acted upon by a force, as...
as a function of time (e.g., the motion of a particle under the influence of a force
Force
In physics, a force is any influence that causes an object to undergo a change in speed, a change in direction, or a change in shape. In other words, a force is that which can cause an object with mass to change its velocity , i.e., to accelerate, or which can cause a flexible object to deform...
). Sometimes the term refers to the differential equations that the system satisfies (e.g., Newton's second law or Euler–Lagrange equations), and sometimes to the solutions to those equations.
Equations of uniformly accelerated linear motion
The equations that apply to bodies moving linearly (in one dimension) with constant accelerationAcceleration
In physics, acceleration is the rate of change of velocity with time. In one dimension, acceleration is the rate at which something speeds up or slows down. However, since velocity is a vector, acceleration describes the rate of change of both the magnitude and the direction of velocity. ...
are often referred to as "SUVAT" equations where the five variables are represented by those letters (s = displacement, u = initial velocity, v = final velocity, a = acceleration, t = time); the five letters may be shown in a different order.
The body is considered between two instants in time: one initial point and one current (or final) point. Problems in kinematics may deal with more than two instants, and several applications of the equations are then required. If a is constant, the differential, a dt, may be integrated over an interval from 0 to
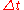 (
( ), to obtain a linear relationship for velocity. Integration of the velocity yields a quadratic relationship for position at the end of the interval.
), to obtain a linear relationship for velocity. Integration of the velocity yields a quadratic relationship for position at the end of the interval.
|
|
where...
and its current state is described by:
|
Note that each of the equations contains four of the five variables.
Thus, in this situation it is sufficient to know three out of the five variables to calculate the remaining two.
Classic version
The equations above are often written in the following form (often informally known as the "suvat" equations):
By substituting (1) into (2), we can get (3), (4) and (5). (6) can be constructed by rearranging (1).
where
- s = the distance between initial and final positions (displacement) (sometimes denoted R or x)
- u = the initial velocity (speed in a given direction)
- v = the final velocity
- a = the constant acceleration
- t = the time taken to move from the initial state to the final state
Examples
Many examples in kinematics involve projectileProjectile
A projectile is any object projected into space by the exertion of a force. Although a thrown baseball is technically a projectile too, the term more commonly refers to a weapon....
s, for example a ball thrown upwards into the air.
Given initial speed u, one can calculate how high the ball will travel before it begins to fall.
The acceleration is local acceleration of gravity g. At this point one must remember that while these quantities appear to be scalars
Scalar (physics)
In physics, a scalar is a simple physical quantity that is not changed by coordinate system rotations or translations , or by Lorentz transformations or space-time translations . This is in contrast to a vector...
, the direction of displacement, speed and acceleration is important. They could in fact be considered as uni-directional vectors. Choosing s to measure up from the ground, the acceleration a must be in fact −g, since the force of gravity acts downwards and therefore also the acceleration on the ball due to it.
At the highest point, the ball will be at rest: therefore v = 0. Using the fifth equation, we have:
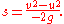
Substituting and cancelling minus signs gives:
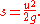
Extension
More complex versions of these equations can include s0 for the initial position of the body, and v0 instead of u for consistency.
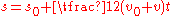

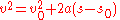
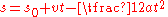
Equations of circular motion
The analogues of the above equations can be written for rotationRotation
A rotation is a circular movement of an object around a center of rotation. A three-dimensional object rotates always around an imaginary line called a rotation axis. If the axis is within the body, and passes through its center of mass the body is said to rotate upon itself, or spin. A rotation...
:

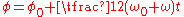
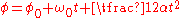
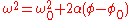
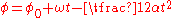
where:
 is the angular acceleration
is the angular accelerationAngular acceleration
Angular acceleration is the rate of change of angular velocity over time. In SI units, it is measured in radians per second squared , and is usually denoted by the Greek letter alpha .- Mathematical definition :...
 is the angular velocity
is the angular velocityAngular velocity
In physics, the angular velocity is a vector quantity which specifies the angular speed of an object and the axis about which the object is rotating. The SI unit of angular velocity is radians per second, although it may be measured in other units such as degrees per second, revolutions per...
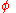 is the angular displacement
is the angular displacementAngular displacement
Angular displacement of a body is the angle in radians through which a point or line has been rotated in a specified sense about a specified axis....
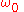 is the initial angular velocity.
is the initial angular velocity.
- t is the time taken to move from the initial state to the final state
Equation 2
By definition:
Hence:
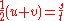
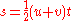
Equation 4
Using equation 1 to substitute u in equation 2 gives: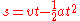
Equation 5
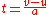
Using equation 2, substitute t with above:
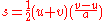

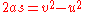



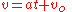

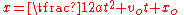

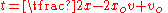
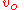 is the body's initial velocity
is the body's initial velocity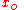 is the body's initial position
is the body's initial position , The velocity at the end of the interval
, The velocity at the end of the interval , the position at the end of the interval (
, the position at the end of the interval ( , the time interval
, the time interval , the constant acceleration, or in the case of bodies moving under the influence of gravity,
, the constant acceleration, or in the case of bodies moving under the influence of gravity,