Theory of tides
Encyclopedia
The theory of tides is the application of continuum mechanics
to interpret and predict the tidal
deformations of planetary and satellite bodies and their atmospheres and oceans, under the gravitational loading of another astronomical body or bodies. It commonly refers to the fluid dynamic motions for the Earth
's ocean
s.
wrote Discourse on the Tides (in Italian: Discorso del flusso e reflusso del mare), a paper in which he tried to explain the occurrence of the tides as the result of the Earth's rotation around the Sun. However, Galileo's theory was, in the later Newtonian
terms, an error. Later analysis over the centuries had led to the current tidal physics.
The forces discussed here apply to body (Earth tides), oceanic and atmospheric tides. Atmospheric tides on Earth, however, tend to be dominated by forcing due to solar heating.
On the planet (or satellite) experiencing tidal motion consider a point at latitude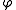
and longitude 
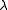at distance 
from the center of mass, then this point can be written in cartesian coordinates as 
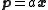where
Let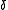
be the declination
and
be the right ascension
of the deforming body, the Moon
for example, then the vector direction is
and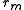
be the orbital distance between the center of masses and 
the mass of the body. Then the force on the point is
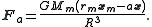
where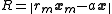
For a circular orbit the angular momentum
centripetal acceleration balances gravity at the planetary center of mass
where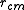
is the distance between the center of mass for the orbit and planet and 
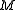is the planetary mass.
Consider the point in the reference fixed without rotation, but translating at a fixed translation with respect to the center of mass of the planet. The body's centripetal force acts on the point so that the total force is
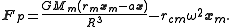
Substituting for center of mass acceleration,
and reordering
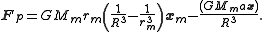
In ocean tidal forcing, the radial force is not significant, the next step is to rewrite the
coefficient. Let 
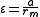then
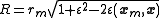
where
is the inner product determining the angle z of the deforming body or Moon from the zenith. This means that
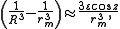
if ε is small. If particle is on the surface of the planet then the local gravity is
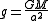and
set
.
which is a small fraction of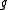
. Note also that force is attractive toward the Moon when the 
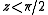and repulsive when 
.
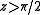This can also be used to derive a tidal potential.
formulated a single set of linear partial differential equation
s, for tidal flow described as a barotropic
two-dimensional sheet flow. Coriolis effect
s are introduced as well as lateral forcing by gravity. Laplace obtained these equations by simplifying the fluid dynamic equations. But they can also be derived from energy integrals via Lagrange's equation.
For a fluid sheet of average
thickness D, the vertical tidal elevation ς, as well as the horizontal velocity components u and v (in the latitude
φ and longitude
λ directions, respectively) satisfy Laplace's tidal equations:
where Ω is the angular frequency
of the planet's rotation, g is the planet's gravitational acceleration at the mean ocean surface, and U is the external gravitational tidal-forcing potential
.
William Thomson (Lord Kelvin)
rewrote Laplace's momentum terms using the curl to find an equation for vorticity. Under certain conditions this can be further rewritten as a conservation of vorticity.
: Darwin's work was based on the lunar theory current in his time. His symbols for the tidal harmonic constituents are still used. Darwin's harmonic developments of the tide-generating forces were later brought up to date with modern developments by A T Doodson
whose development of the tide generating potential (TGP) in harmonic form was carried out and published in 1921: Doodson distinguished 388 tidal frequencies. Doodson's analysis of 1921 was based on the then-latest lunar theory
of E W Brown
.
Doodson devised a practical system for specifying the different harmonic components of the tide-generating potential, the Doodson Numbers, a system still in use.
Since the mid-twentieth century further analysis has generated many more terms than Doodson's 388. About 62 constituents are of sufficient size to be considered for possible use in marine tide prediction, but sometimes many less even than that can predict tides to useful accuracy. The calculations of tide predictions using the harmonic constituents are laborious, and from the 1870s to about the 1960s they were carried out using a mechanical tide-predicting machine
, a special-purpose form of analog computer
now superseded in this work by digital electronic computers that can be programmed to carry out the same computations.
. Amplitudes of tidal constituents are given below for the following example locations:
Continuum mechanics
Continuum mechanics is a branch of mechanics that deals with the analysis of the kinematics and the mechanical behavior of materials modelled as a continuous mass rather than as discrete particles...
to interpret and predict the tidal
Tide
Tides are the rise and fall of sea levels caused by the combined effects of the gravitational forces exerted by the moon and the sun and the rotation of the Earth....
deformations of planetary and satellite bodies and their atmospheres and oceans, under the gravitational loading of another astronomical body or bodies. It commonly refers to the fluid dynamic motions for the Earth
Earth
Earth is the third planet from the Sun, and the densest and fifth-largest of the eight planets in the Solar System. It is also the largest of the Solar System's four terrestrial planets...
's ocean
Ocean
An ocean is a major body of saline water, and a principal component of the hydrosphere. Approximately 71% of the Earth's surface is covered by ocean, a continuous body of water that is customarily divided into several principal oceans and smaller seas.More than half of this area is over 3,000...
s.
Origin of theory
In 1616, Galileo GalileiGalileo Galilei
Galileo Galilei , was an Italian physicist, mathematician, astronomer, and philosopher who played a major role in the Scientific Revolution. His achievements include improvements to the telescope and consequent astronomical observations and support for Copernicanism...
wrote Discourse on the Tides (in Italian: Discorso del flusso e reflusso del mare), a paper in which he tried to explain the occurrence of the tides as the result of the Earth's rotation around the Sun. However, Galileo's theory was, in the later Newtonian
Newtonian
Newtonian refers to the work of Isaac Newton, in particular:* Newtonian mechanics, also known as classical mechanics* Newtonian telescope, a type of reflecting telescope* Newtonian cosmology* Newtonian dynamics...
terms, an error. Later analysis over the centuries had led to the current tidal physics.
Tidal forcing
The forces discussed here apply to body (Earth tides), oceanic and atmospheric tides. Atmospheric tides on Earth, however, tend to be dominated by forcing due to solar heating.
On the planet (or satellite) experiencing tidal motion consider a point at latitude
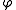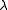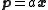and longitude at distance from the center of mass, then this point can be written in cartesian coordinates as whereLet
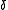be the declinationDeclination
In astronomy, declination is one of the two coordinates of the equatorial coordinate system, the other being either right ascension or hour angle. Declination in astronomy is comparable to geographic latitude, but projected onto the celestial sphere. Declination is measured in degrees north and...
and
be the right ascensionRight ascension
Right ascension is the astronomical term for one of the two coordinates of a point on the celestial sphere when using the equatorial coordinate system. The other coordinate is the declination.-Explanation:...
of the deforming body, the Moon
Moon
The Moon is Earth's only known natural satellite,There are a number of near-Earth asteroids including 3753 Cruithne that are co-orbital with Earth: their orbits bring them close to Earth for periods of time but then alter in the long term . These are quasi-satellites and not true moons. For more...
for example, then the vector direction is
and
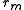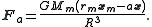
be the orbital distance between the center of masses and the mass of the body. Then the force on the point iswhere
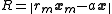
For a circular orbit the angular momentum
centripetal acceleration balances gravity at the planetary center of masswhere
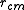is the distance between the center of mass for the orbit and planet and 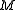is the planetary mass.Consider the point in the reference fixed without rotation, but translating at a fixed translation with respect to the center of mass of the planet. The body's centripetal force acts on the point so that the total force is
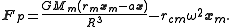
Substituting for center of mass acceleration,
and reordering
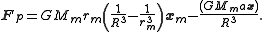
In ocean tidal forcing, the radial force is not significant, the next step is to rewrite the
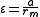coefficient. Let then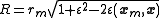where
is the inner product determining the angle z of the deforming body or Moon from the zenith. This means that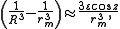if ε is small. If particle is on the surface of the planet then the local gravity is
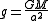andset
.which is a small fraction of
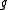. Note also that force is attractive toward the Moon when the 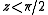and repulsive when 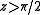.This can also be used to derive a tidal potential.
Laplace's tidal equations
in 1776, Pierre-Simon LaplacePierre-Simon Laplace
Pierre-Simon, marquis de Laplace was a French mathematician and astronomer whose work was pivotal to the development of mathematical astronomy and statistics. He summarized and extended the work of his predecessors in his five volume Mécanique Céleste...
formulated a single set of linear partial differential equation
Partial differential equation
In mathematics, partial differential equations are a type of differential equation, i.e., a relation involving an unknown function of several independent variables and their partial derivatives with respect to those variables...
s, for tidal flow described as a barotropic
Barotropic
In meteorology, a barotropic atmosphere is one in which the pressure depends only on the density and vice versa, so that isobaric surfaces are also isopycnic surfaces . The isobaric surfaces will also be isothermal surfaces, hence the geostrophic wind is independent of height...
two-dimensional sheet flow. Coriolis effect
Coriolis effect
In physics, the Coriolis effect is a deflection of moving objects when they are viewed in a rotating reference frame. In a reference frame with clockwise rotation, the deflection is to the left of the motion of the object; in one with counter-clockwise rotation, the deflection is to the right...
s are introduced as well as lateral forcing by gravity. Laplace obtained these equations by simplifying the fluid dynamic equations. But they can also be derived from energy integrals via Lagrange's equation.
For a fluid sheet of average
Average
In mathematics, an average, or central tendency of a data set is a measure of the "middle" value of the data set. Average is one form of central tendency. Not all central tendencies should be considered definitions of average....
thickness D, the vertical tidal elevation ς, as well as the horizontal velocity components u and v (in the latitude
Latitude
In geography, the latitude of a location on the Earth is the angular distance of that location south or north of the Equator. The latitude is an angle, and is usually measured in degrees . The equator has a latitude of 0°, the North pole has a latitude of 90° north , and the South pole has a...
φ and longitude
Longitude
Longitude is a geographic coordinate that specifies the east-west position of a point on the Earth's surface. It is an angular measurement, usually expressed in degrees, minutes and seconds, and denoted by the Greek letter lambda ....
λ directions, respectively) satisfy Laplace's tidal equations:
where Ω is the angular frequency
Angular frequency
In physics, angular frequency ω is a scalar measure of rotation rate. Angular frequency is the magnitude of the vector quantity angular velocity...
of the planet's rotation, g is the planet's gravitational acceleration at the mean ocean surface, and U is the external gravitational tidal-forcing potential
Potential
*In linguistics, the potential mood*The mathematical study of potentials is known as potential theory; it is the study of harmonic functions on manifolds...
.
William Thomson (Lord Kelvin)
William Thomson, 1st Baron Kelvin
William Thomson, 1st Baron Kelvin OM, GCVO, PC, PRS, PRSE, was a mathematical physicist and engineer. At the University of Glasgow he did important work in the mathematical analysis of electricity and formulation of the first and second laws of thermodynamics, and did much to unify the emerging...
rewrote Laplace's momentum terms using the curl to find an equation for vorticity. Under certain conditions this can be further rewritten as a conservation of vorticity.
Harmonic analysis
Laplace's improvements in theory were substantial, but they still left prediction in an approximate state. This position changed in the 1860s when the local circumstances of tidal phenomena were more fully brought into account by William Thomson's application of Fourier analysis to the tidal motions. Thomson's work in this field was then further developed and extended by George DarwinGeorge Darwin
Sir George Howard Darwin, FRS was an English astronomer and mathematician.-Biography:Darwin was born at Down House, Kent, the second son and fifth child of Charles and Emma Darwin...
: Darwin's work was based on the lunar theory current in his time. His symbols for the tidal harmonic constituents are still used. Darwin's harmonic developments of the tide-generating forces were later brought up to date with modern developments by A T Doodson
Arthur Thomas Doodson
-Biography:He was born at Boothstown, Salford, the son of cotton-mill manager Thomas Doodson. He was educated at Rochdale secondary school and then in 1908 entered Liverpool University, graduating in both chemistry and mathematics . He was profoundly deaf and found it difficult to get a job but...
whose development of the tide generating potential (TGP) in harmonic form was carried out and published in 1921: Doodson distinguished 388 tidal frequencies. Doodson's analysis of 1921 was based on the then-latest lunar theory
Lunar theory
Lunar theory attempts to account for the motions of the Moon. There are many irregularities in the Moon's motion, and many attempts have been made over a long history to account for them. After centuries of being heavily problematic, the lunar motions are nowadays modelled to a very high degree...
of E W Brown
Ernest William Brown
Ernest William Brown FRS was a British mathematician and astronomer, who spent the majority of his career working in the United States....
.
Doodson devised a practical system for specifying the different harmonic components of the tide-generating potential, the Doodson Numbers, a system still in use.
Since the mid-twentieth century further analysis has generated many more terms than Doodson's 388. About 62 constituents are of sufficient size to be considered for possible use in marine tide prediction, but sometimes many less even than that can predict tides to useful accuracy. The calculations of tide predictions using the harmonic constituents are laborious, and from the 1870s to about the 1960s they were carried out using a mechanical tide-predicting machine
Tide-predicting machine
A tide-predicting machine was a special-purpose mechanical analog computer of the late 19th and early 20th centuries, constructed and set up to predict the ebb and flow of sea tides and the irregular variations in their heights – which change in mixtures of rhythms, that never repeat...
, a special-purpose form of analog computer
Analog computer
An analog computer is a form of computer that uses the continuously-changeable aspects of physical phenomena such as electrical, mechanical, or hydraulic quantities to model the problem being solved...
now superseded in this work by digital electronic computers that can be programmed to carry out the same computations.
Tidal constituents
Tidal constituents combine to give an endlessly-varying aggregate because of their different and incommensurable frequencies: the effect is visualized in an animation of the American Mathematical Society illustrating the way in which the components used to be mechanically combined in the tide-predicting machineTide-predicting machine
A tide-predicting machine was a special-purpose mechanical analog computer of the late 19th and early 20th centuries, constructed and set up to predict the ebb and flow of sea tides and the irregular variations in their heights – which change in mixtures of rhythms, that never repeat...
. Amplitudes of tidal constituents are given below for the following example locations:
- ME Eastport,
- MS Biloxi,
- PR San Juan,
- AK Kodiak,
- CA San Francisco, and
- HI Hilo.
Higher harmonics |
Darwin |
Period |
Phase |
Doodson coefs |
Doodson |
Amplitude at example location (cm) |
NOAA |
||||||||
Species |
Symbol |
(hr) |
rate(°/hr) |
n1 (L) | n2 (m) | n3 (y) | n4 (mp) | number |
ME |
MS |
PR |
AK |
CA |
HI |
order |
| Shallow water overtides of principal lunar | M4 | 6.210300601 | 57.9682084 | 4 | 455.555 | 6.0 | 0.6 | 0.9 | 2.3 | 5 | |||||
| Shallow water overtides of principal lunar | M6 | 4.140200401 | 86.9523127 | 6 | 655.555 | 5.1 | 0.1 | 1.0 | 7 | ||||||
| Shallow water terdiurnal | MK3 | 8.177140247 | 44.0251729 | 3 | 1 | 365.555 | 0.5 | 1.9 | 8 | ||||||
| Shallow water overtides of principal solar | S4 | 6 | 60 | 4 | 4 | -4 | 491.555 | 0.1 | 9 | ||||||
| Shallow water quarter diurnal | MN4 | 6.269173724 | 57.4238337 | 4 | -1 | 1 | 445.655 | 2.3 | 0.3 | 0.9 | 10 | ||||
| Shallow water overtides of principal solar | S6 | 4 | 90 | 6 | 6 | -6 | * | 0.1 | 12 | ||||||
| Lunar terdiurnal | M3 | 8.280400802 | 43.4761563 | 3 | 355.555 | 0.5 | 32 | ||||||||
| Shallow water terdiurnal | 2"MK3 | 8.38630265 | 42.9271398 | 3 | -1 | 345.555 | 0.5 | 0.5 | 1.4 | 34 | |||||
| Shallow water eighth diurnal | M8 | 3.105150301 | 115.9364166 | 8 | 855.555 | 0.5 | 0.1 | 36 | |||||||
| Shallow water quarter diurnal | MS4 | 6.103339275 | 58.9841042 | 4 | 2 | -2 | 473.555 | 1.8 | 0.6 | 1.0 | 37 | ||||
Semi-diurnal |
Darwin |
Period |
Phase |
Doodson coefs |
Doodson |
Amplitude at example location (cm) |
NOAA |
||||||||
| Species | Symbol |
(hr) |
(°/hr) |
n1 (L) | n2 (m) | n3 (y) | n4 (mp) | number |
ME |
MS |
PR |
AK |
CA |
HI |
order |
| Principal lunar semidiurnal | M2 | 12.4206012 | 28.9841042 | 2 | 255.555 | 268.7 | 3.9 | 15.9 | 97.3 | 58.0 | 23.0 | 1 | |||
| Principal solar semidiurnal | S2 | 12 | 30 | 2 | 2 | -2 | 273.555 | 42.0 | 3.3 | 2.1 | 32.5 | 13.7 | 9.2 | 2 | |
| Larger lunar elliptic semidiurnal | N2 | 12.65834751 | 28.4397295 | 2 | -1 | 1 | 245.655 | 54.3 | 1.1 | 3.7 | 20.1 | 12.3 | 4.4 | 3 | |
| Larger lunar evectional | ν2 | 12.62600509 | 28.5125831 | 2 | -1 | 2 | -1 | 247.455 | 12.6 | 0.2 | 0.8 | 3.9 | 2.6 | 0.9 | 11 |
| Variational | MU2 | 12.8717576 | 27.9682084 | 2 | -2 | 2 | 237.555 | 2.0 | 0.1 | 0.5 | 2.2 | 0.7 | 0.8 | 13 | |
| Lunar elliptical semidiurnal second-order | 2"N2 | 12.90537297 | 27.8953548 | 2 | -2 | 2 | 235.755 | 6.5 | 0.1 | 0.5 | 2.4 | 1.4 | 0.6 | 14 | |
| Smaller lunar evectional | λ2 | 12.22177348 | 29.4556253 | 2 | 1 | -2 | 1 | 263.655 | 5.3 | 0.1 | 0.7 | 0.6 | 0.2 | 16 | |
| Larger solar elliptic | T2 | 12.01644934 | 29.9589333 | 2 | 2 | -3 | 272.555 | 3.7 | 0.2 | 0.1 | 1.9 | 0.9 | 0.6 | 27 | |
| Smaller solar elliptic | R2 | 11.98359564 | 30.0410667 | 2 | 2 | -1 | 274.555 | 0.9 | 0.2 | 0.1 | 0.1 | 28 | |||
| Shallow water semidiurnal | 2SM2 | 11.60695157 | 31.0158958 | 2 | 4 | -4 | 291.555 | 0.5 | 31 | ||||||
| Smaller lunar elliptic semidiurnal | L2 | 12.19162085 | 29.5284789 | 2 | 1 | -1 | 265.455 | 13.5 | 0.1 | 0.5 | 2.4 | 1.6 | 0.5 | 33 | |
| Lunisolar semidiurnal | K2 | 11.96723606 | 30.0821373 | 2 | 2 | 275.555 | 11.6 | 0.9 | 0.6 | 9.0 | 4.0 | 2.8 | 35 | ||
Diurnal |
Darwin |
Period |
Phase |
Doodson coefs |
Doodson |
Amplitude at example location (cm) |
NOAA |
||||||||
| Species | Symbol |
(hr) |
(°/hr) |
n1 (L) | n2 (m) | n3 (y) | n4 (mp) | number |
ME |
MS |
PR |
AK |
CA |
HI |
order |
| Lunar diurnal | K1 | 23.93447213 | 15.0410686 | 1 | 1 | 165.555 | 15.6 | 16.2 | 9.0 | 39.8 | 36.8 | 16.7 | '4 | ||
| Lunar diurnal | O1 | 25.81933871 | 13.9430356 | 1 | -1 | 145.555 | 11.9 | 16.9 | 7.7 | 25.9 | 23.0 | 9.2 | 6 | ||
| Lunar diurnal | OO1 | 22.30608083 | 16.1391017 | 1 | 3 | 185.555 | 0.5 | 0.7 | 0.4 | 1.2 | 1.1 | 0.7 | 15 | ||
| Solar diurnal | S1 | 24 | 15 | 1 | 1 | -1 | 164.555 | 1.0 | 0.5 | 1.2 | 0.7 | 0.3 | 17 | ||
| Smaller lunar elliptic diurnal | M1 | 24.84120241 | 14.4920521 | 1 | 155.555 | 0.6 | 1.2 | 0.5 | 1.4 | 1.1 | 0.5 | 18 | |||
| Smaller lunar elliptic diurnal | J1 | 23.09848146 | 15.5854433 | 1 | 2 | -1 | 175.455 | 0.9 | 1.3 | 0.6 | 2.3 | 1.9 | 1.1 | 19 | |
| Larger lunar evectional diurnal | ρ | 26.72305326 | 13.4715145 | 1 | -2 | 2 | -1 | 137.455 | 0.3 | 0.6 | 0.3 | 0.9 | 0.9 | 0.3 | 25 |
| Larger lunar elliptic diurnal | Q1 | 26.868350 | 13.3986609 | 1 | -2 | 1 | 135.655 | 2.0 | 3.3 | 1.4 | 4.7 | 4.0 | 1.6 | 26 | |
| Larger elliptic diurnal | 2Q1 | 28.00621204 | 12.8542862 | 1 | -3 | 2 | 125.755 | 0.3 | 0.4 | 0.2 | 0.7 | 0.4 | 0.2 | 29 | |
| Solar diurnal | P1 | 24.06588766 | 14.9589314 | 1 | 1 | -2 | 163.555 | 5.2 | 5.4 | 2.9 | 12.6 | 11.6 | 5.1 | 30 | |
Long period |
Darwin |
Period |
Phase |
Doodson coefs |
Doodson |
Amplitude at example location (cm) |
NOAA |
||||||||
| Species | Symbol |
(hr) |
(°/hr) |
n1 (L) | n2 (m) | n3 (y) | n4 (mp) | number |
ME |
MS |
PR |
AK |
CA |
HI |
order |
| Lunar monthly | Mm | 661.3111655 | 0.5443747 | 0 | 1 | -1 | 65.455 | 0.7 | 1.9 | 20 | |||||
| Solar semiannual | Ssa | 4383.076325 | 0.0821373 | 0 | 2 | 57.555 | 1.6 | 2.1 | 1.5 | 3.9 | 21 | ||||
| Solar annual | Sa | 8766.15265 | 0.0410686 | 0 | 1 | 56.555 | 5.5 | 7.8 | 3.8 | 4.3 | 22 | ||||
| Lunisolar synodic fortnightly | Msf | 354.3670666 | 1.0158958 | 0 | 2 | -2 | 73.555 | 1.5 | 23 | ||||||
| Lunisolar fortnightly | Mf | 327.8599387 | 1.0980331 | 0 | 2 | 75.555 | 1.4 | 2.0 | 0.7 | 24 | |||||