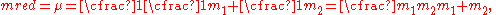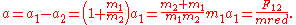Reduced mass
Encyclopedia
Reduced mass is the "effective" inertial mass appearing in the two-body problem
of Newtonian mechanics. This is a quantity with the unit
of mass, which allows the two-body problem to be solved as if it were a one-body problem. Note however that the mass determining the gravitational force is not reduced. In the computation one mass can be replaced by the reduced mass, if this is compensated by replacing the other mass by the sum of both masses.
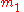and the other with mass 
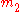, the equivalent one-body problem, with the position of one body with respect to the other as the unknown, is that of a single body of mass
where the force on this mass is given by the force between the two bodies.
The reduced mass is always less than or equal to the mass of each body and is half of the harmonic mean
of the two masses.
This can be proven easily. Use Newton's second law, the force exerted by body 2 on body 1 is
The force exerted by body 1 on body 2 is
According to Newton's third law, the force that body 2 exerts on body 1 is equal and opposite to the force that body 1 exerts on body 2: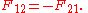
Therefore,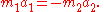
and
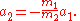
The relative acceleration between the two bodies is given by
So we conclude that body 1 moves with respect to the position of body 2 as a body of mass equal to the reduced mass.
Alternatively, a Lagrangian description of the two-body problem gives a Lagrangian of
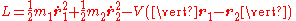
where
are the mass and position vector of the 
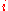th particle, respectively. The potential energy 
takes this functional dependence as it is only dependent on the absolute distance between the particles. If we define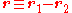 
and let the centre of mass coincide with our origin in this reference frame, i.e. 
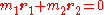, then
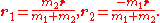
Then substituting above gives a new Lagrangian
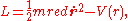
where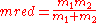
, the reduced mass. Thus we have reduced the two-body problem to that of one body.
The reduced mass is frequently denoted by the Greek letter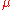
; note however that the standard gravitational parameter
is also denoted by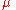
.
In the case of the gravitational potential energy
we find that the position of the first body with respect to the second is governed by the same differential equation as the position of a body with the reduced mass orbiting a body with a mass equal to the sum of the two masses, because
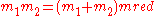
"Reduced mass" may also refer more generally to an algebraic
term of the form
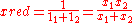
that simplifies an equation of the form
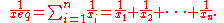
The reduced mass is typically used as a relationship between two system elements in parallel, such as resistors; whether these be in the electrical, thermal, hydraulic, or mechanical domains. This relationship is determined by the physical properties of the elements as well as the continuity equation
linking them.
e, the change in kinetic energy can be written as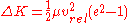
, where vrel is the relative velocity of the bodies before collision
.
Two-body problem
In classical mechanics, the two-body problem is to determine the motion of two point particles that interact only with each other. Common examples include a satellite orbiting a planet, a planet orbiting a star, two stars orbiting each other , and a classical electron orbiting an atomic nucleus In...
of Newtonian mechanics. This is a quantity with the unit
Units of measurement
A unit of measurement is a definite magnitude of a physical quantity, defined and adopted by convention and/or by law, that is used as a standard for measurement of the same physical quantity. Any other value of the physical quantity can be expressed as a simple multiple of the unit of...
of mass, which allows the two-body problem to be solved as if it were a one-body problem. Note however that the mass determining the gravitational force is not reduced. In the computation one mass can be replaced by the reduced mass, if this is compensated by replacing the other mass by the sum of both masses.
Derivation
Given two bodies, one with mass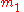 and the other with mass 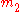, the equivalent one-body problem, with the position of one body with respect to the other as the unknown, is that of a single body of mass
where the force on this mass is given by the force between the two bodies.
The reduced mass is always less than or equal to the mass of each body and is half of the harmonic mean
Harmonic mean
In mathematics, the harmonic mean is one of several kinds of average. Typically, it is appropriate for situations when the average of rates is desired....
of the two masses.
This can be proven easily. Use Newton's second law, the force exerted by body 2 on body 1 is
The force exerted by body 1 on body 2 is
According to Newton's third law, the force that body 2 exerts on body 1 is equal and opposite to the force that body 1 exerts on body 2:
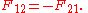
Therefore,
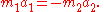
and
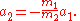
The relative acceleration between the two bodies is given by
So we conclude that body 1 moves with respect to the position of body 2 as a body of mass equal to the reduced mass.
Alternatively, a Lagrangian description of the two-body problem gives a Lagrangian of
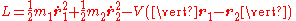
where
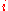are the mass and position vector of the th particle, respectively. The potential energy takes this functional dependence as it is only dependent on the absolute distance between the particles. If we define 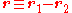and let the centre of mass coincide with our origin in this reference frame, i.e. 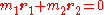, then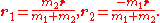Then substituting above gives a new Lagrangian
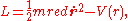
where
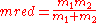, the reduced mass. Thus we have reduced the two-body problem to that of one body.The reduced mass is frequently denoted by the Greek letter
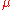; note however that the standard gravitational parameterStandard gravitational parameter
In astrodynamics, the standard gravitational parameter μ of a celestial body is the product of the gravitational constant G and the mass M of the body.\mu=GM \ The SI units of the standard gravitational parameter are m3s−2....
is also denoted by
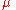.In the case of the gravitational potential energy
we find that the position of the first body with respect to the second is governed by the same differential equation as the position of a body with the reduced mass orbiting a body with a mass equal to the sum of the two masses, because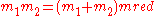"Reduced mass" may also refer more generally to an algebraic
Algebraic
Algebraic may refer to any subject within the algebra branch of mathematics and related branches like algebraic geometry and algebraic topology.Algebraic may also refer to:...
term of the form
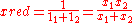
that simplifies an equation of the form
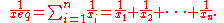
The reduced mass is typically used as a relationship between two system elements in parallel, such as resistors; whether these be in the electrical, thermal, hydraulic, or mechanical domains. This relationship is determined by the physical properties of the elements as well as the continuity equation
Continuity equation
A continuity equation in physics is a differential equation that describes the transport of a conserved quantity. Since mass, energy, momentum, electric charge and other natural quantities are conserved under their respective appropriate conditions, a variety of physical phenomena may be described...
linking them.
Other uses
Reduced mass crops up in a multitude of two-body problems. In a collision with a coefficient of restitutionCoefficient of restitution
The coefficient of restitution of two colliding objects is a fractional value representing the ratio of speeds after and before an impact, taken along the line of the impact...
e, the change in kinetic energy can be written as
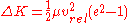, where vrel is the relative velocity of the bodies before collisionCollision
A collision is an isolated event which two or more moving bodies exert forces on each other for a relatively short time.Although the most common colloquial use of the word "collision" refers to accidents in which two or more objects collide, the scientific use of the word "collision" implies...
.