Body	μ (km3s−2)
Sun Sun The Sun is the star at the center of the Solar System. It is almost perfectly spherical and consists of hot plasma interwoven with magnetic fields...
Mercury Mercury (planet) Mercury is the innermost and smallest planet in the Solar System, orbiting the Sun once every 87.969 Earth days. The orbit of Mercury has the highest eccentricity of all the Solar System planets, and it has the smallest axial tilt. It completes three rotations about its axis for every two orbits...
Venus Venus Venus is the second planet from the Sun, orbiting it every 224.7 Earth days. The planet is named after Venus, the Roman goddess of love and beauty. After the Moon, it is the brightest natural object in the night sky, reaching an apparent magnitude of −4.6, bright enough to cast shadows...
Earth Earth Earth is the third planet from the Sun, and the densest and fifth-largest of the eight planets in the Solar System. It is also the largest of the Solar System's four terrestrial planets...
Moon Moon The Moon is Earth's only known natural satellite,There are a number of near-Earth asteroids including 3753 Cruithne that are co-orbital with Earth: their orbits bring them close to Earth for periods of time but then alter in the long term . These are quasi-satellites and not true moons. For more...
Mars Mars Mars is the fourth planet from the Sun in the Solar System. The planet is named after the Roman god of war, Mars. It is often described as the "Red Planet", as the iron oxide prevalent on its surface gives it a reddish appearance...
Ceres 1 Ceres Ceres, formally 1 Ceres, is the smallest identified dwarf planet in the Solar System and the only one in the asteroid belt. With a diameter of about 950 km, Ceres is by far the largest and most-massive asteroid, comprising about a third of the mass of the asteroid belt. Discovered on 1 January 1801...
Jupiter Jupiter Jupiter is the fifth planet from the Sun and the largest planet within the Solar System. It is a gas giant with mass one-thousandth that of the Sun but is two and a half times the mass of all the other planets in our Solar System combined. Jupiter is classified as a gas giant along with Saturn,...
Saturn Saturn Saturn is the sixth planet from the Sun and the second largest planet in the Solar System, after Jupiter. Saturn is named after the Roman god Saturn, equated to the Greek Cronus , the Babylonian Ninurta and the Hindu Shani. Saturn's astronomical symbol represents the Roman god's sickle.Saturn,...
Uranus Uranus Uranus is the seventh planet from the Sun. It has the third-largest planetary radius and fourth-largest planetary mass in the Solar System. It is named after the ancient Greek deity of the sky Uranus , the father of Cronus and grandfather of Zeus...
Neptune Neptune Neptune is the eighth and farthest planet from the Sun in the Solar System. Named for the Roman god of the sea, it is the fourth-largest planet by diameter and the third largest by mass. Neptune is 17 times the mass of Earth and is slightly more massive than its near-twin Uranus, which is 15 times...
Pluto Pluto Pluto, formal designation 134340 Pluto, is the second-most-massive known dwarf planet in the Solar System and the tenth-most-massive body observed directly orbiting the Sun...
Eris Eris (dwarf planet) Eris, formal designation 136199 Eris, is the most massive known dwarf planet in the Solar System and the ninth most massive body known to orbit the Sun directly...

In astrodynamics

Astrodynamics

Orbital mechanics or astrodynamics is the application of ballistics and celestial mechanics to the practical problems concerning the motion of rockets and other spacecraft. The motion of these objects is usually calculated from Newton's laws of motion and Newton's law of universal gravitation. It...

, the standard gravitational parameter μ of a celestial body

Celestial Body

Celestial Body is a Croatian film directed by Lukas Nola. It was released in 2000....

 is the product of the gravitational constant

Gravitational constant

The gravitational constant, denoted G, is an empirical physical constant involved in the calculation of the gravitational attraction between objects with mass. It appears in Newton's law of universal gravitation and in Einstein's theory of general relativity. It is also known as the universal...

 G and the mass M of the body.


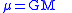
The SI

Si

Si, si, or SI may refer to :- Measurement, mathematics and science :* International System of Units , the modern international standard version of the metric system...

 units of the standard gravitational parameter are m

Metre

The metre , symbol m, is the base unit of length in the International System of Units . Originally intended to be one ten-millionth of the distance from the Earth's equator to the North Pole , its definition has been periodically refined to reflect growing knowledge of metrology...

³s

Second

The second is a unit of measurement of time, and is the International System of Units base unit of time. It may be measured using a clock....

⁻².

Small body orbiting a central body

Under standard assumptions in astrodynamics we have:
where m is the mass of the orbiting body

Orbiting body

In astrodynamics, an orbiting body is a body that orbits a primary body .The orbiting body is properly referred to as the secondary body.It is less massive than the primary body ....

, M is the mass of the central body

Central body

In astrodynamics a central body is a body that is being orbited by an secondary body, or satellite .The central body is properly referred to as the primary body.Under standard assumptions in astrodynamics:...

, and G is the standard gravitational parameter of the larger body.

For all circular orbit

Circular orbit

A circular orbit is the orbit at a fixed distance around any point by an object rotating around a fixed axis.Below we consider a circular orbit in astrodynamics or celestial mechanics under standard assumptions...

s around a given central body:
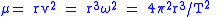
where r is the orbit radius

Radius

In classical geometry, a radius of a circle or sphere is any line segment from its center to its perimeter. By extension, the radius of a circle or sphere is the length of any such segment, which is half the diameter. If the object does not have an obvious center, the term may refer to its...

, v is the orbital speed

Orbital speed

The orbital speed of a body, generally a planet, a natural satellite, an artificial satellite, or a multiple star, is the speed at which it orbits around the barycenter of a system, usually around a more massive body...

, ω is the angular speed, and T is the orbital period

Orbital period

The orbital period is the time taken for a given object to make one complete orbit about another object.When mentioned without further qualification in astronomy this refers to the sidereal period of an astronomical object, which is calculated with respect to the stars.There are several kinds of...

.

The last equality has a very simple generalization to elliptic orbit

Elliptic orbit

In astrodynamics or celestial mechanics an elliptic orbit is a Kepler orbit with the eccentricity less than 1; this includes the special case of a circular orbit, with eccentricity equal to zero. In a stricter sense, it is a Kepler orbit with the eccentricity greater than 0 and less than 1 . In a...

s:
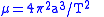
where a is the semi-major axis

Semi-major axis

The major axis of an ellipse is its longest diameter, a line that runs through the centre and both foci, its ends being at the widest points of the shape...

. See Kepler's third law.

For all parabolic trajectories

Parabolic trajectory

In astrodynamics or celestial mechanics a parabolic trajectory is a Kepler orbit with the eccentricity equal to 1. When moving away from the source it is called an escape orbit, otherwise a capture orbit...

 rv² is constant and equal to 2μ. For elliptic and hyperbolic orbits μ = 2a|ε|, where ε is the specific orbital energy

Specific orbital energy

In the gravitational two-body problem, the specific orbital energy \epsilon\,\! of two orbiting bodies is the constant sum of their mutual potential energy and their total kinetic energy , divided by the reduced mass...

.

Two bodies orbiting each other

In the more general case where the bodies need not be a large one and a small one (the two-body problem

Two-body problem

In classical mechanics, the two-body problem is to determine the motion of two point particles that interact only with each other. Common examples include a satellite orbiting a planet, a planet orbiting a star, two stars orbiting each other , and a classical electron orbiting an atomic nucleus In...

), we define:

• the vector r is the position of one body relative to the other
• r, v, and in the case of an elliptic orbit
  Elliptic orbit
  In astrodynamics or celestial mechanics an elliptic orbit is a Kepler orbit with the eccentricity less than 1; this includes the special case of a circular orbit, with eccentricity equal to zero. In a stricter sense, it is a Kepler orbit with the eccentricity greater than 0 and less than 1 . In a...
  
  , the semi-major axis
  Semi-major axis
  The major axis of an ellipse is its longest diameter, a line that runs through the centre and both foci, its ends being at the widest points of the shape...
  
   a, are defined accordingly (hence r is the distance)
• μ = Gm₁ + Gm₂ = μ₁ + μ₂, where m₁ and m₂ are the masses of the two bodies.

Then:

• for circular orbit
  Circular orbit
  A circular orbit is the orbit at a fixed distance around any point by an object rotating around a fixed axis.Below we consider a circular orbit in astrodynamics or celestial mechanics under standard assumptions...
  
  s, rv² = r³ω² = 4π²r³/T² = μ
• for elliptic orbit
  Elliptic orbit
  In astrodynamics or celestial mechanics an elliptic orbit is a Kepler orbit with the eccentricity less than 1; this includes the special case of a circular orbit, with eccentricity equal to zero. In a stricter sense, it is a Kepler orbit with the eccentricity greater than 0 and less than 1 . In a...
  
  s, 4π²a³/T² = μ (with a expressed in AU and T in years, and with M the total mass relative to that of the Sun, we get a³/T² = M)
• for parabolic trajectories
  Parabolic trajectory
  In astrodynamics or celestial mechanics a parabolic trajectory is a Kepler orbit with the eccentricity equal to 1. When moving away from the source it is called an escape orbit, otherwise a capture orbit...
  
  , rv² is constant and equal to 2μ
• for elliptic and hyperbolic orbits, μ is twice the semi-major axis times the absolute value of the specific orbital energy
  Specific orbital energy
  In the gravitational two-body problem, the specific orbital energy \epsilon\,\! of two orbiting bodies is the constant sum of their mutual potential energy and their total kinetic energy , divided by the reduced mass...
  
  , where the latter is defined as the total energy of the system divided by the reduced mass
  Reduced mass
  Reduced mass is the "effective" inertial mass appearing in the two-body problem of Newtonian mechanics. This is a quantity with the unit of mass, which allows the two-body problem to be solved as if it were a one-body problem. Note however that the mass determining the gravitational force is not...
  
  .

Terminology and accuracy

Note that the reduced mass

Reduced mass

Reduced mass is the "effective" inertial mass appearing in the two-body problem of Newtonian mechanics. This is a quantity with the unit of mass, which allows the two-body problem to be solved as if it were a one-body problem. Note however that the mass determining the gravitational force is not...

 is also denoted by .

The value for the Earth

Earth

Earth is the third planet from the Sun, and the densest and fifth-largest of the eight planets in the Solar System. It is also the largest of the Solar System's four terrestrial planets...

 is called the geocentric gravitational constant and equals . Thus the uncertainty is 1 to , much smaller than the uncertainties in G and M separately (1 to each).

The value for the Sun

Sun

The Sun is the star at the center of the Solar System. It is almost perfectly spherical and consists of hot plasma interwoven with magnetic fields...

is called the heliocentric gravitational constant and equals .