Exchange interaction
Encyclopedia
In physics
, the exchange interaction is a quantum mechanical effect without classical
analog which increases or decreases the expectation value
of the energy
or distance
between two or more identical particles
when their wave function
s overlap. For example, the exchange interaction results in identical particles with spatially symmetric wave functions (boson
s) appearing "closer together" than would be expected of distinguishable particles, and in identical particles with spatially antisymmetric wave functions (fermion
s) appearing "farther apart". It is the mechanism that is responsible for some types of ferromagnetism
, among other consequences.
Although sometimes erroneously described as a force
, the exchange interaction is a purely quantum mechanical effect without any analog in classical mechanics. It is due to the wave function of indistinguishable particles
being subject to exchange symmetry
, that is, the wave function describing two particles that cannot be distinguished must be either unchanged (symmetric) or inverted in sign (antisymmetric) if the labels of the two particles are changed.
For example, if the expectation value of the distance between two particles in a spatially symmetric or antisymmetric state is calculated, the exchange interaction may be seen.
Both boson
s and fermion
s can experience the exchange interaction provided that the particles in question are indistinguishable.
Exchange interaction effects were discovered independently by physicists Werner Heisenberg
and P. A. M. Dirac in 1926.
The exchange interaction is sometimes called the exchange force, but it is not a true force and should not be confused with the exchange force
s produced by the exchange of force carrier
s, such as the electromagnetic force produced between two electrons by the exchange of a photon
, or the strong force between two quark
s produced by the exchange of a gluon
.
of quantum field theory
demands that all particles with half-integer
spin
behave as fermions and all particles with integer
spin behave as bosons. Multiple bosons may occupy the same quantum state; by the Pauli exclusion principle
, however, no two fermions can occupy the same state. Since electron
s have spin 1/2, they are fermions. This means that the overall wave function of a system must be antisymmetric when two electrons are exchanged, i.e. interchanged with respect to both spatial and spin coordinates. First, however, exchange will be explained with the neglect of spin.
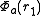for the first electron and 
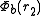for the second electron. We assume that 
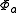and 
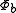are orthogonal, and that each corresponds to an energy eigenstate of its electron. Now, we may construct a wave function for the overall system in position space by using an antisymmetric combination of the product wave functions in position space:
Alternatively, we may also construct the overall position-space wave function by using a symmetric combination of the product wave functions in position space:
Treating the exchange interaction in the hydrogen molecule by the perturbation method, the overall Hamiltonian
is:
= 
+ 
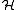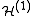
where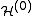
= 
(
+ 
)
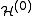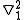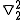
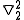and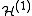 
= 
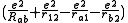
Two eigenvalues for the system energy are found:
where the E+ is the spatially symmetric solution and E- is the spatially antisymmetric solution. A variational calculation yields similar results.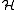
can be diagonalized by using the position-space functions given by Eqs. (1) and (2). In Eq. (3), C is the Coulomb integral, B is the overlap integral, and Jex is the exchange integral. These integrals are given by:
The terms in parentheses in Eqs. (4) and (6) correspond to: proton-proton repulsion (Rab), electron-electron repulsion (r12), and electron-proton attraction (ra1/a2/b1/b2).
Although in the hydrogen molecule the exchange integral, Eq. (6), is negative, Heisenberg first suggested that it changes sign at some critical ratio of internuclear distance to mean radial extension of the atomic orbital.
To obtain the overall wave function, these spin combinations have to be coupled with Eqs. (1) and (2). The resulting overall wave functions, called spin-orbitals, are written as Slater determinant
s. When the orbital wave function is symmetrical the spin one must be anti-symmetrical and vice versa. Accordingly, E+ above corresponds to the spatially symmetric/spin-singlet solution and E- to the spatially antisymmetric/spin-triplet solution.
J. H. Van Vleck
presented the following analysis:
Dirac pointed out that the critical features of the exchange interaction could be obtained in an elementary way by neglecting the first two terms on the right-hand side of Eq. (9), thereby considering the two electrons as simply having their spins coupled by a potential of the form:
It follows that the exchange interaction Hamiltonian between two electrons in orbitals Φa and Φb can be written in terms of their spin momenta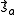
and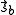 
. This is named the Heisenberg Exchange Hamiltonian
or the Heisenberg-Dirac Hamiltonian in the older literature:
Jab is not the same as the quantity labeled Jex in Eq. (6). Rather, Jab, which is termed the exchange constant, is a function of Eqs. (4), (5), and (6), namely,
However, with orthogonal orbitals (in which B = 0), for example with different orbitals in the same atom, Jab = Jex.
in materials in which the electrons are considered localized in the Heitler-London model of chemical bonding, but this model of ferromagnetism has severe limitations in solids (see below). If Jab is negative, the interaction favors electrons with antiparallel spins, potentially causing antiferromagnetism
. The sign of Jab is essentially determined by the relative sizes of Jex and the product of CB2. This can be deduced from the expression for the difference between the energies of the triplet and singlet states, E- - E+:
Although these consequences of the exchange interaction are magnetic in nature, the cause is not; it is due primarily to electric repulsion and the Pauli exclusion principle. Indeed, in general, the direct magnetic interaction between a pair of electrons (due to their electron magnetic moments) is negligibly small compared to this electric interaction.
Exchange energy splittings are very elusive to calculate for molecular systems at large internuclear distances. However, analytical formulae have been worked out for the hydrogen molecular ion
(see references herein).
Normally, exchange interactions are very short-ranged, confined to electrons in orbitals on the same atom (intra-atomic exchange) or nearest neighbor atoms (direct exchange) but longer-ranged interactions can occur via intermediary atoms and this is termed Superexchange
.
The 1/2 factor is introduced because the interaction between the same two atoms is counted twice in performing the sums. Note that the J in Eq.(14) is the exchange constant Jab above not the exchange integral Jex. The exchange integral Jex is related to yet another quantity, called the exchange stiffness constant (A) which serves as a characteristic of a ferromagnetic material. The relationship is dependent on the crystal structure. For a simple cubic lattice with lattice parameter
,
For a body-centered cubic lattice,
and for a face-centered cubic lattice,
The form of Eq. (14) corresponds identically to the Ising [statistical mechanical] model
of ferromagnetism except that in the Ising model, the dot product of the two spin angular momenta is replaced by the scalar product SijSji. The Ising model was invented by Wilhelm Lenz in 1920 and solved for the one-dimensional case by his doctoral student Ernst Ising in 1925. The energy of the Ising model is defined to be:
(VB), theory of chemical bonding, it is an adequate model for explaining the magnetic properties of electrically insulating narrow-band ionic and covalent non-molecular solids where this picture of the bonding is reasonable. Nevertheless, theoretical evaluations of the exchange integral for non-molecular solids that display metallic conductivity in which the electrons responsible for the ferromagnetism are itinerant (e.g. iron, nickel, and cobalt) have historically been either of the wrong sign or much too small in magnitude to account for the experimentally determined exchange constant (e.g. as estimated from the Curie temperatures via TC ≈ 2⟨J⟩/3kB where ⟨J⟩ is the exchange interaction averaged over all sites). The Heisenberg model thus cannot explain the observed ferromagnetism in these materials. In these cases, a delocalized, or Hund-Mulliken-Bloch (molecular orbital/band) description, for the electron wave functions is more realistic. Accordingly, the Stoner model of ferromagnetism is more applicable. In the Stoner model, the spin-only magnetic moment (in Bohr magnetons) per atom in a ferromagnet is given by the difference between the number of electrons per atom in the majority spin and minority spin states. The Stoner model thus permits non-integral values for the spin-only magnetic moment per atom. However, with ferromagnets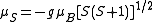
(g = 2.0023 ≈ 2) tends to overestimate the total spin-only magnetic moment
per atom. For example, a net magnetic moment of 0.54 μB per atom for Nickel metal is predicted by the Stoner model, which is very close to the 0.61 Bohr magnetons calculated based on the metal's observed saturation magnetic induction, its density, and its atomic weight. By contrast, an isolated Ni atom (electron configuration = 3d84s2) in a cubic crystal field will have two unpaired electrons of the same spin (hence,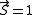
) and would thus be expected to have in the localized electron model a total spin magnetic moment of 
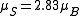(but the measured spin-only magnetic moment along one axis, the physical observable, will be given by 
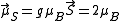). Generally, valence s and p electrons are best considered delocalized, while 4f electrons are localized and 5f and 3d/4d electrons are intermediate, depending on the particular internuclear distances. In the case of substances where both delocalized and localized electrons contribute to the magnetic properties (e.g. rare-earth systems), the Ruderman-Kittel-Kasuya-Yosida (RKKY) model is the currently accepted mechanism.
Physics
Physics is a natural science that involves the study of matter and its motion through spacetime, along with related concepts such as energy and force. More broadly, it is the general analysis of nature, conducted in order to understand how the universe behaves.Physics is one of the oldest academic...
, the exchange interaction is a quantum mechanical effect without classical
Classical mechanics
In physics, classical mechanics is one of the two major sub-fields of mechanics, which is concerned with the set of physical laws describing the motion of bodies under the action of a system of forces...
analog which increases or decreases the expectation value
Expectation value (quantum mechanics)
In quantum mechanics, the expectation value is the predicted mean value of the result of an experiment. Despite the name, it is not the most probable value of a measurement...
of the energy
Energy
In physics, energy is an indirectly observed quantity. It is often understood as the ability a physical system has to do work on other physical systems...
or distance
Distance
Distance is a numerical description of how far apart objects are. In physics or everyday discussion, distance may refer to a physical length, or an estimation based on other criteria . In mathematics, a distance function or metric is a generalization of the concept of physical distance...
between two or more identical particles
Identical particles
Identical particles, or indistinguishable particles, are particles that cannot be distinguished from one another, even in principle. Species of identical particles include elementary particles such as electrons, and, with some clauses, composite particles such as atoms and molecules.There are two...
when their wave function
Wavefunction
Not to be confused with the related concept of the Wave equationA wave function or wavefunction is a probability amplitude in quantum mechanics describing the quantum state of a particle and how it behaves. Typically, its values are complex numbers and, for a single particle, it is a function of...
s overlap. For example, the exchange interaction results in identical particles with spatially symmetric wave functions (boson
Boson
In particle physics, bosons are subatomic particles that obey Bose–Einstein statistics. Several bosons can occupy the same quantum state. The word boson derives from the name of Satyendra Nath Bose....
s) appearing "closer together" than would be expected of distinguishable particles, and in identical particles with spatially antisymmetric wave functions (fermion
Fermion
In particle physics, a fermion is any particle which obeys the Fermi–Dirac statistics . Fermions contrast with bosons which obey Bose–Einstein statistics....
s) appearing "farther apart". It is the mechanism that is responsible for some types of ferromagnetism
Ferromagnetism
Ferromagnetism is the basic mechanism by which certain materials form permanent magnets, or are attracted to magnets. In physics, several different types of magnetism are distinguished...
, among other consequences.
Although sometimes erroneously described as a force
Force
In physics, a force is any influence that causes an object to undergo a change in speed, a change in direction, or a change in shape. In other words, a force is that which can cause an object with mass to change its velocity , i.e., to accelerate, or which can cause a flexible object to deform...
, the exchange interaction is a purely quantum mechanical effect without any analog in classical mechanics. It is due to the wave function of indistinguishable particles
Identical particles
Identical particles, or indistinguishable particles, are particles that cannot be distinguished from one another, even in principle. Species of identical particles include elementary particles such as electrons, and, with some clauses, composite particles such as atoms and molecules.There are two...
being subject to exchange symmetry
Exchange symmetry
Exchange symmetry is derived from a fundamental postulate of quantum statistics, which states that no observable physical quantity should change after exchanging two identical particles...
, that is, the wave function describing two particles that cannot be distinguished must be either unchanged (symmetric) or inverted in sign (antisymmetric) if the labels of the two particles are changed.
For example, if the expectation value of the distance between two particles in a spatially symmetric or antisymmetric state is calculated, the exchange interaction may be seen.
Both boson
Boson
In particle physics, bosons are subatomic particles that obey Bose–Einstein statistics. Several bosons can occupy the same quantum state. The word boson derives from the name of Satyendra Nath Bose....
s and fermion
Fermion
In particle physics, a fermion is any particle which obeys the Fermi–Dirac statistics . Fermions contrast with bosons which obey Bose–Einstein statistics....
s can experience the exchange interaction provided that the particles in question are indistinguishable.
Exchange interaction effects were discovered independently by physicists Werner Heisenberg
Werner Heisenberg
Werner Karl Heisenberg was a German theoretical physicist who made foundational contributions to quantum mechanics and is best known for asserting the uncertainty principle of quantum theory...
and P. A. M. Dirac in 1926.
The exchange interaction is sometimes called the exchange force, but it is not a true force and should not be confused with the exchange force
Exchange force
In physics the term exchange force has been used to describe two distinct concepts which should not be confused.-Exchange of force carriers in particle physics:...
s produced by the exchange of force carrier
Force carrier
In particle physics, quantum field theories such as the Standard Model describe nature in terms of fields. Each field has a complementary description as the set of particles of a particular type...
s, such as the electromagnetic force produced between two electrons by the exchange of a photon
Photon
In physics, a photon is an elementary particle, the quantum of the electromagnetic interaction and the basic unit of light and all other forms of electromagnetic radiation. It is also the force carrier for the electromagnetic force...
, or the strong force between two quark
Quark
A quark is an elementary particle and a fundamental constituent of matter. Quarks combine to form composite particles called hadrons, the most stable of which are protons and neutrons, the components of atomic nuclei. Due to a phenomenon known as color confinement, quarks are never directly...
s produced by the exchange of a gluon
Gluon
Gluons are elementary particles which act as the exchange particles for the color force between quarks, analogous to the exchange of photons in the electromagnetic force between two charged particles....
.
Exchange Interactions between localized electron magnetic moments
Quantum mechanical particles are classified as bosons or fermions. The spin-statistics theoremSpin-statistics theorem
In quantum mechanics, the spin-statistics theorem relates the spin of a particle to the particle statistics it obeys. The spin of a particle is its intrinsic angular momentum...
of quantum field theory
Quantum field theory
Quantum field theory provides a theoretical framework for constructing quantum mechanical models of systems classically parametrized by an infinite number of dynamical degrees of freedom, that is, fields and many-body systems. It is the natural and quantitative language of particle physics and...
demands that all particles with half-integer
Half-integer
In mathematics, a half-integer is a number of the formn + 1/2,where n is an integer. For example,are all half-integers. Note that a half of an integer is not always a half-integer: half of an even integer is an integer but not a half-integer...
spin
Spin (physics)
In quantum mechanics and particle physics, spin is a fundamental characteristic property of elementary particles, composite particles , and atomic nuclei.It is worth noting that the intrinsic property of subatomic particles called spin and discussed in this article, is related in some small ways,...
behave as fermions and all particles with integer
Integer
The integers are formed by the natural numbers together with the negatives of the non-zero natural numbers .They are known as Positive and Negative Integers respectively...
spin behave as bosons. Multiple bosons may occupy the same quantum state; by the Pauli exclusion principle
Pauli exclusion principle
The Pauli exclusion principle is the quantum mechanical principle that no two identical fermions may occupy the same quantum state simultaneously. A more rigorous statement is that the total wave function for two identical fermions is anti-symmetric with respect to exchange of the particles...
, however, no two fermions can occupy the same state. Since electron
Electron
The electron is a subatomic particle with a negative elementary electric charge. It has no known components or substructure; in other words, it is generally thought to be an elementary particle. An electron has a mass that is approximately 1/1836 that of the proton...
s have spin 1/2, they are fermions. This means that the overall wave function of a system must be antisymmetric when two electrons are exchanged, i.e. interchanged with respect to both spatial and spin coordinates. First, however, exchange will be explained with the neglect of spin.
Exchange of spatial coordinates
Taking a hydrogen molecule-like system (i.e. one with two electrons), we may attempt to model the state of each electron by first assuming the electrons behave independently, and taking wave functions in position space of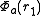 for the first electron and 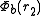for the second electron. We assume that 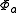and 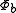are orthogonal, and that each corresponds to an energy eigenstate of its electron. Now, we may construct a wave function for the overall system in position space by using an antisymmetric combination of the product wave functions in position space:Alternatively, we may also construct the overall position-space wave function by using a symmetric combination of the product wave functions in position space:
Treating the exchange interaction in the hydrogen molecule by the perturbation method, the overall Hamiltonian
Hamiltonian (quantum mechanics)
In quantum mechanics, the Hamiltonian H, also Ȟ or Ĥ, is the operator corresponding to the total energy of the system. Its spectrum is the set of possible outcomes when one measures the total energy of a system...
is:
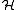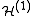
= + where
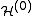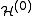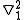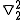
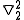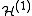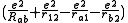
= ( + ) and = Two eigenvalues for the system energy are found:
where the E+ is the spatially symmetric solution and E- is the spatially antisymmetric solution. A variational calculation yields similar results.
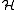can be diagonalized by using the position-space functions given by Eqs. (1) and (2). In Eq. (3), C is the Coulomb integral, B is the overlap integral, and Jex is the exchange integral. These integrals are given by:The terms in parentheses in Eqs. (4) and (6) correspond to: proton-proton repulsion (Rab), electron-electron repulsion (r12), and electron-proton attraction (ra1/a2/b1/b2).
Although in the hydrogen molecule the exchange integral, Eq. (6), is negative, Heisenberg first suggested that it changes sign at some critical ratio of internuclear distance to mean radial extension of the atomic orbital.
Inclusion of spin
The symmetric and antisymmetric combinations in Eqs. (1) and (2) did not include the spin variables (α = spin-up; β = spin down); there are also antisymmetric and symmetric combinations of the spin variables:To obtain the overall wave function, these spin combinations have to be coupled with Eqs. (1) and (2). The resulting overall wave functions, called spin-orbitals, are written as Slater determinant
Slater determinant
In quantum mechanics, a Slater determinant is an expression that describes the wavefunction of a multi-fermionic system that satisfies anti-symmetry requirements and consequently the Pauli exclusion principle by changing sign upon exchange of fermions . It is named for its discoverer, John C...
s. When the orbital wave function is symmetrical the spin one must be anti-symmetrical and vice versa. Accordingly, E+ above corresponds to the spatially symmetric/spin-singlet solution and E- to the spatially antisymmetric/spin-triplet solution.
J. H. Van Vleck
John Hasbrouck van Vleck
John Hasbrouck Van Vleck was an American physicist and mathematician, co-awarded the 1977 Nobel Prize in Physics, for his contributions to the understanding of the behavior of electrons in magnetic solids....
presented the following analysis:
- The potential energy of the interaction between the two electrons in orthogonal orbitals can be represented by a matrix, say Eex. From Eq. (3), the characteristic values of this matrix are C ± Jex. The characteristic values of a matrix are its diagonal elements after it is converted to a diagonal matrix. Now, the characteristic values of the square of the magnitude of the resultant spin
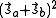is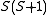 
. The characteristic values of the matrices 
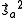and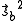 
are each 
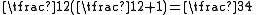and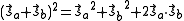 
. The characteristic values of the scalar product 
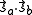are 
and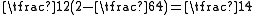 
, corresponding to the spin-singlet (S = 0) - and spin-triplet (S = 1) states. From Eq. (3) and the aforementioned relations, the matrix Eex is seen to have the characteristic value C + Jex when
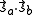has the characteristic value -3/4 (i.e. when S = 0; the spatially symmetric/spin-singlet state). Alternatively, it has the characteristic value C - Jex when 
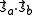has the characteristic value +1/4 (i.e. when S = 1; the spatially antisymmetric/spin-triplet state). Therefore,
- and, hence,
- where the spin momenta are given as
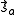and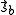 
.
Dirac pointed out that the critical features of the exchange interaction could be obtained in an elementary way by neglecting the first two terms on the right-hand side of Eq. (9), thereby considering the two electrons as simply having their spins coupled by a potential of the form:
It follows that the exchange interaction Hamiltonian between two electrons in orbitals Φa and Φb can be written in terms of their spin momenta
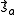and 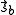. This is named the Heisenberg Exchange HamiltonianHeisenberg model (classical)
The Classical Heisenberg model is the n = 3 case of the n-vector model, one of the models used in statistical physics to model ferromagnetism, and other phenomena.-Definition:...
or the Heisenberg-Dirac Hamiltonian in the older literature:
Jab is not the same as the quantity labeled Jex in Eq. (6). Rather, Jab, which is termed the exchange constant, is a function of Eqs. (4), (5), and (6), namely,
However, with orthogonal orbitals (in which B = 0), for example with different orbitals in the same atom, Jab = Jex.
Effects of exchange
If Jab is positive the exchange energy favors electrons with parallel spins; this is a primary cause of ferromagnetismFerromagnetism
Ferromagnetism is the basic mechanism by which certain materials form permanent magnets, or are attracted to magnets. In physics, several different types of magnetism are distinguished...
in materials in which the electrons are considered localized in the Heitler-London model of chemical bonding, but this model of ferromagnetism has severe limitations in solids (see below). If Jab is negative, the interaction favors electrons with antiparallel spins, potentially causing antiferromagnetism
Antiferromagnetism
In materials that exhibit antiferromagnetism, the magnetic moments of atoms or molecules, usuallyrelated to the spins of electrons, align in a regular pattern with neighboring spins pointing in opposite directions. This is, like ferromagnetism and ferrimagnetism, a manifestation of ordered magnetism...
. The sign of Jab is essentially determined by the relative sizes of Jex and the product of CB2. This can be deduced from the expression for the difference between the energies of the triplet and singlet states, E- - E+:
Although these consequences of the exchange interaction are magnetic in nature, the cause is not; it is due primarily to electric repulsion and the Pauli exclusion principle. Indeed, in general, the direct magnetic interaction between a pair of electrons (due to their electron magnetic moments) is negligibly small compared to this electric interaction.
Exchange energy splittings are very elusive to calculate for molecular systems at large internuclear distances. However, analytical formulae have been worked out for the hydrogen molecular ion
Hydrogen molecular ion
The hydrogen molecular ion, dihydrogen cation, or H2+, is the simplest molecular ion. It is composed of two positively-charged protons and one negatively-charged electron, and can be formed from ionization of a neutral hydrogen molecule...
(see references herein).
Normally, exchange interactions are very short-ranged, confined to electrons in orbitals on the same atom (intra-atomic exchange) or nearest neighbor atoms (direct exchange) but longer-ranged interactions can occur via intermediary atoms and this is termed Superexchange
Superexchange
Superexchange is the strong antiferromagnetic coupling between two next-to-nearest neighbor cations through a non-magnetic anion. In this way, it differs from direct exchange in which there is coupling between nearest neighbor cations not involving an intermediary anion...
.
Direct exchange interactions in solids
In a crystal, generalization of the Heisenberg Hamiltonian in which the sum is taken over the exchange Hamiltonians for all the (i,j) pairs of atoms of the many-electron system gives:.The 1/2 factor is introduced because the interaction between the same two atoms is counted twice in performing the sums. Note that the J in Eq.(14) is the exchange constant Jab above not the exchange integral Jex. The exchange integral Jex is related to yet another quantity, called the exchange stiffness constant (A) which serves as a characteristic of a ferromagnetic material. The relationship is dependent on the crystal structure. For a simple cubic lattice with lattice parameter
,For a body-centered cubic lattice,
and for a face-centered cubic lattice,
The form of Eq. (14) corresponds identically to the Ising [statistical mechanical] model
Ising model
The Ising model is a mathematical model of ferromagnetism in statistical mechanics. The model consists of discrete variables called spins that can be in one of two states . The spins are arranged in a graph , and each spin interacts with its nearest neighbors...
of ferromagnetism except that in the Ising model, the dot product of the two spin angular momenta is replaced by the scalar product SijSji. The Ising model was invented by Wilhelm Lenz in 1920 and solved for the one-dimensional case by his doctoral student Ernst Ising in 1925. The energy of the Ising model is defined to be:
Limitations of the Heisenberg Hamiltonian and the localized electron model in solids
Because the Heisenberg Hamiltonian presumes the electrons involved in the exchange coupling are localized in the context of the Heitler-London, or valence bondValence bond theory
In chemistry, valence bond theory is one of two basic theories, along with molecular orbital theory, that were developed to use the methods of quantum mechanics to explain chemical bonding. It focuses on how the atomic orbitals of the dissociated atoms combine to give individual chemical bonds...
(VB), theory of chemical bonding, it is an adequate model for explaining the magnetic properties of electrically insulating narrow-band ionic and covalent non-molecular solids where this picture of the bonding is reasonable. Nevertheless, theoretical evaluations of the exchange integral for non-molecular solids that display metallic conductivity in which the electrons responsible for the ferromagnetism are itinerant (e.g. iron, nickel, and cobalt) have historically been either of the wrong sign or much too small in magnitude to account for the experimentally determined exchange constant (e.g. as estimated from the Curie temperatures via TC ≈ 2⟨J⟩/3kB where ⟨J⟩ is the exchange interaction averaged over all sites). The Heisenberg model thus cannot explain the observed ferromagnetism in these materials. In these cases, a delocalized, or Hund-Mulliken-Bloch (molecular orbital/band) description, for the electron wave functions is more realistic. Accordingly, the Stoner model of ferromagnetism is more applicable. In the Stoner model, the spin-only magnetic moment (in Bohr magnetons) per atom in a ferromagnet is given by the difference between the number of electrons per atom in the majority spin and minority spin states. The Stoner model thus permits non-integral values for the spin-only magnetic moment per atom. However, with ferromagnets
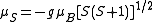(g = 2.0023 ≈ 2) tends to overestimate the total spin-only magnetic momentSpin magnetic moment
-Basis for spin magnetic moments:A spin magnetic moment is induced by all charged particles. The electron is an example of one such charged particle. A spin magnetic moment is created because a particle has physical properties known as spin and electric charge. The spin within classical physics...
per atom. For example, a net magnetic moment of 0.54 μB per atom for Nickel metal is predicted by the Stoner model, which is very close to the 0.61 Bohr magnetons calculated based on the metal's observed saturation magnetic induction, its density, and its atomic weight. By contrast, an isolated Ni atom (electron configuration = 3d84s2) in a cubic crystal field will have two unpaired electrons of the same spin (hence,
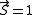) and would thus be expected to have in the localized electron model a total spin magnetic moment of 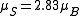(but the measured spin-only magnetic moment along one axis, the physical observable, will be given by 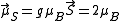). Generally, valence s and p electrons are best considered delocalized, while 4f electrons are localized and 5f and 3d/4d electrons are intermediate, depending on the particular internuclear distances. In the case of substances where both delocalized and localized electrons contribute to the magnetic properties (e.g. rare-earth systems), the Ruderman-Kittel-Kasuya-Yosida (RKKY) model is the currently accepted mechanism.See also
- Double-exchange mechanismDouble-exchange mechanismThe double-exchange mechanism is a type of a magnetic exchange that may arise between ions in different oxidation state. First proposed by Clarence Zener, this theory that predicts the relative ease with which an electron may be exchanged between two species, and has important implications for...
- Exchange symmetryExchange symmetryExchange symmetry is derived from a fundamental postulate of quantum statistics, which states that no observable physical quantity should change after exchanging two identical particles...
- Pauli exclusion principlePauli exclusion principleThe Pauli exclusion principle is the quantum mechanical principle that no two identical fermions may occupy the same quantum state simultaneously. A more rigorous statement is that the total wave function for two identical fermions is anti-symmetric with respect to exchange of the particles...
- Slater determinantSlater determinantIn quantum mechanics, a Slater determinant is an expression that describes the wavefunction of a multi-fermionic system that satisfies anti-symmetry requirements and consequently the Pauli exclusion principle by changing sign upon exchange of fermions . It is named for its discoverer, John C...
- SuperexchangeSuperexchangeSuperexchange is the strong antiferromagnetic coupling between two next-to-nearest neighbor cations through a non-magnetic anion. In this way, it differs from direct exchange in which there is coupling between nearest neighbor cations not involving an intermediary anion...
- Holstein–Herring method