Eigenspinor
Encyclopedia
In quantum mechanics
, eigenspinors are thought of as basis vectors representing the general spin state of a particle. Strictly speaking, they are not vectors at all, but in fact spinors. For a single spin 1/2 particle, they can be defined as the eigenvectors of the Pauli matrices
.
of a particle or collection of particles is quantized
. In particular, all particles have either half integer or integer spin. In the most general case, the eigenspinors for a system can be quite complicated. If you have a collection of Avogadro's number
of particles, each one with two (or more) possible spin states, there would be no hope of writing down a complete set of eigenspinors. However, eigenspinors are very useful when dealing with the spins of a very small number of particles.
, 
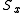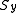, and 
. For a spin 1/2 particle, there are only two possible eigenstates of spin: spin up, and spin down. Spin up is denoted as the column matrix:
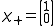
and spin down is
.
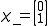Each component of the angular momentum thus has two eigenspinors. By convention, the z direction is chosen as having the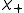
and 
states as its eigenspinors. The eigenspinors for the other two directions follow from this convention:
:
:
:
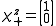
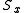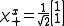
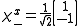
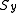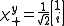
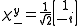
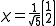. To determine the probability of finding the particle in a spin up state, we simply multiply the state of the particle by the adjoint of the eigenspinor matrix representing spin up, and square the result. Thus, the eigenspinor allows us to sample the part of the particle's state that is in the same direction as the eigenspinor. First we multiply:
.
Now, we simply square this value to obtain the probability of the particle being found in a spin up state:
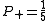
, orthonormal
basis. This means that any state can be written as a linear combination
of the basis
spinors.
The eigenspinors are eigenvectors of the Pauli matrices in the case of a single spin 1/2 particle.
Quantum mechanics
Quantum mechanics, also known as quantum physics or quantum theory, is a branch of physics providing a mathematical description of much of the dual particle-like and wave-like behavior and interactions of energy and matter. It departs from classical mechanics primarily at the atomic and subatomic...
, eigenspinors are thought of as basis vectors representing the general spin state of a particle. Strictly speaking, they are not vectors at all, but in fact spinors. For a single spin 1/2 particle, they can be defined as the eigenvectors of the Pauli matrices
Pauli matrices
The Pauli matrices are a set of three 2 × 2 complex matrices which are Hermitian and unitary. Usually indicated by the Greek letter "sigma" , they are occasionally denoted with a "tau" when used in connection with isospin symmetries...
.
General eigenspinors
In quantum mechanics, the spinSpin (physics)
In quantum mechanics and particle physics, spin is a fundamental characteristic property of elementary particles, composite particles , and atomic nuclei.It is worth noting that the intrinsic property of subatomic particles called spin and discussed in this article, is related in some small ways,...
of a particle or collection of particles is quantized
Quantization (physics)
In physics, quantization is the process of explaining a classical understanding of physical phenomena in terms of a newer understanding known as "quantum mechanics". It is a procedure for constructing a quantum field theory starting from a classical field theory. This is a generalization of the...
. In particular, all particles have either half integer or integer spin. In the most general case, the eigenspinors for a system can be quite complicated. If you have a collection of Avogadro's number
Avogadro's number
In chemistry and physics, the Avogadro constant is defined as the ratio of the number of constituent particles N in a sample to the amount of substance n through the relationship NA = N/n. Thus, it is the proportionality factor that relates the molar mass of an entity, i.e...
of particles, each one with two (or more) possible spin states, there would be no hope of writing down a complete set of eigenspinors. However, eigenspinors are very useful when dealing with the spins of a very small number of particles.
The spin 1/2 particle
The simplest and most illuminating example of eigenspinors is for a single spin 1/2 particle. A particle's spin has three components, corresponding to the three spatial dimensions: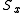, , 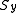and . For a spin 1/2 particle, there are only two possible eigenstates of spin: spin up, and spin down. Spin up is denoted as the column matrix: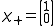and spin down is
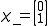.Each component of the angular momentum thus has two eigenspinors. By convention, the z direction is chosen as having the
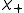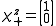
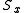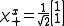
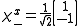
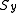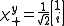
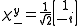
and states as its eigenspinors. The eigenspinors for the other two directions follow from this convention::::Example usage
Suppose there is a spin 1/2 particle in a state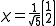. To determine the probability of finding the particle in a spin up state, we simply multiply the state of the particle by the adjoint of the eigenspinor matrix representing spin up, and square the result. Thus, the eigenspinor allows us to sample the part of the particle's state that is in the same direction as the eigenspinor. First we multiply:.Now, we simply square this value to obtain the probability of the particle being found in a spin up state:
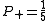
Properties
Each set of eigenspinors forms a completeComplete space
In mathematical analysis, a metric space M is called complete if every Cauchy sequence of points in M has a limit that is also in M or, alternatively, if every Cauchy sequence in M converges in M....
, orthonormal
Orthonormal basis
In mathematics, particularly linear algebra, an orthonormal basis for inner product space V with finite dimension is a basis for V whose vectors are orthonormal. For example, the standard basis for a Euclidean space Rn is an orthonormal basis, where the relevant inner product is the dot product of...
basis. This means that any state can be written as a linear combination
Linear combination
In mathematics, a linear combination is an expression constructed from a set of terms by multiplying each term by a constant and adding the results...
of the basis
Basis (linear algebra)
In linear algebra, a basis is a set of linearly independent vectors that, in a linear combination, can represent every vector in a given vector space or free module, or, more simply put, which define a "coordinate system"...
spinors.
The eigenspinors are eigenvectors of the Pauli matrices in the case of a single spin 1/2 particle.