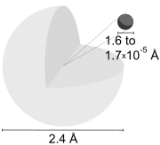
Hydrogen atom
Encyclopedia
Atom
The atom is a basic unit of matter that consists of a dense central nucleus surrounded by a cloud of negatively charged electrons. The atomic nucleus contains a mix of positively charged protons and electrically neutral neutrons...
of the chemical element hydrogen
Hydrogen
Hydrogen is the chemical element with atomic number 1. It is represented by the symbol H. With an average atomic weight of , hydrogen is the lightest and most abundant chemical element, constituting roughly 75% of the Universe's chemical elemental mass. Stars in the main sequence are mainly...
. The electrically
Electric charge
Electric charge is a physical property of matter that causes it to experience a force when near other electrically charged matter. Electric charge comes in two types, called positive and negative. Two positively charged substances, or objects, experience a mutual repulsive force, as do two...
neutral atom contains a single positively-charged proton
Proton
The proton is a subatomic particle with the symbol or and a positive electric charge of 1 elementary charge. One or more protons are present in the nucleus of each atom, along with neutrons. The number of protons in each atom is its atomic number....
and a single negatively-charged electron
Electron
The electron is a subatomic particle with a negative elementary electric charge. It has no known components or substructure; in other words, it is generally thought to be an elementary particle. An electron has a mass that is approximately 1/1836 that of the proton...
bound to the nucleus by the Coulomb force. The most abundant
Abundance of the chemical elements
The abundance of a chemical element measures how relatively common the element is, or how much of the element is present in a given environment by comparison to all other elements...
isotope
Isotope
Isotopes are variants of atoms of a particular chemical element, which have differing numbers of neutrons. Atoms of a particular element by definition must contain the same number of protons but may have a distinct number of neutrons which differs from atom to atom, without changing the designation...
, hydrogen-1, protium, or light hydrogen, contains no neutron
Neutron
The neutron is a subatomic hadron particle which has the symbol or , no net electric charge and a mass slightly larger than that of a proton. With the exception of hydrogen, nuclei of atoms consist of protons and neutrons, which are therefore collectively referred to as nucleons. The number of...
s; other isotopes of hydrogen
Isotopes of hydrogen
Hydrogen has three naturally occurring isotopes, sometimes denoted 1H, 2H, and 3H. Other, highly unstable nuclei have been synthesized in the laboratory but not observed in nature. The most stable radioisotope is tritium, with a half-life of 12.32 years...
, such as deuterium
Deuterium
Deuterium, also called heavy hydrogen, is one of two stable isotopes of hydrogen. It has a natural abundance in Earth's oceans of about one atom in of hydrogen . Deuterium accounts for approximately 0.0156% of all naturally occurring hydrogen in Earth's oceans, while the most common isotope ...
, contain one or more neutrons. The formulas below are valid for all three isotopes of hydrogen, however slightly different values of the Rydberg constant (correction formula given below) must be used for each hydrogen isotope.
The hydrogen atom has special significance in quantum mechanics
Quantum mechanics
Quantum mechanics, also known as quantum physics or quantum theory, is a branch of physics providing a mathematical description of much of the dual particle-like and wave-like behavior and interactions of energy and matter. It departs from classical mechanics primarily at the atomic and subatomic...
and quantum field theory
Quantum field theory
Quantum field theory provides a theoretical framework for constructing quantum mechanical models of systems classically parametrized by an infinite number of dynamical degrees of freedom, that is, fields and many-body systems. It is the natural and quantitative language of particle physics and...
as a simple two-body problem
Two-body problem
In classical mechanics, the two-body problem is to determine the motion of two point particles that interact only with each other. Common examples include a satellite orbiting a planet, a planet orbiting a star, two stars orbiting each other , and a classical electron orbiting an atomic nucleus In...
physical system which has yielded many simple analytical
Closed-form expression
In mathematics, an expression is said to be a closed-form expression if it can be expressed analytically in terms of a bounded number of certain "well-known" functions...
solutions in closed-form.
In 1914, Niels Bohr
Niels Bohr
Niels Henrik David Bohr was a Danish physicist who made foundational contributions to understanding atomic structure and quantum mechanics, for which he received the Nobel Prize in Physics in 1922. Bohr mentored and collaborated with many of the top physicists of the century at his institute in...
obtained the spectral frequencies of the hydrogen atom after making a number of simplifying assumptions. These assumptions, the cornerstones of the Bohr model
Bohr model
In atomic physics, the Bohr model, introduced by Niels Bohr in 1913, depicts the atom as a small, positively charged nucleus surrounded by electrons that travel in circular orbits around the nucleus—similar in structure to the solar system, but with electrostatic forces providing attraction,...
, were not fully correct but did yield the correct energy answers. Bohr's results for the frequencies and underlying energy values were confirmed by the full quantum-mechanical analysis which uses the Schrödinger equation
Schrödinger equation
The Schrödinger equation was formulated in 1926 by Austrian physicist Erwin Schrödinger. Used in physics , it is an equation that describes how the quantum state of a physical system changes in time....
, as was shown in 1925–1926. The solution to the Schrödinger equation for hydrogen is analytical
Closed-form expression
In mathematics, an expression is said to be a closed-form expression if it can be expressed analytically in terms of a bounded number of certain "well-known" functions...
. From this, the hydrogen energy levels and thus the frequencies of the hydrogen spectral line
Spectral line
A spectral line is a dark or bright line in an otherwise uniform and continuous spectrum, resulting from a deficiency or excess of photons in a narrow frequency range, compared with the nearby frequencies.- Types of line spectra :...
s can be calculated. The solution of the Schrödinger equation goes much further than the Bohr model however, because it also yields the shape of the electron's wave function ("orbital") for the various possible quantum-mechanical states, thus explaining the anisotropic character of atomic bonds.
The Schrödinger equation also applies to more complicated atoms and molecule
Molecule
A molecule is an electrically neutral group of at least two atoms held together by covalent chemical bonds. Molecules are distinguished from ions by their electrical charge...
s. However, in most such cases the solution is not analytical and either computer calculations are necessary or simplifying assumptions must be made.
Solution of Schrödinger equation: Overview of results
The solution of the Schrödinger equation (wave equations) for the hydrogen atom uses the fact that the Coulomb potentialCoulomb's law
Coulomb's law or Coulomb's inverse-square law, is a law of physics describing the electrostatic interaction between electrically charged particles. It was first published in 1785 by French physicist Charles Augustin de Coulomb and was essential to the development of the theory of electromagnetism...
produced by the nucleus is isotropic (it is radially symmetric in space and only depends on the distance to the nucleus). Although the resulting energy eigenfunctions (the orbitals) are not necessarily isotropic themselves, their dependence on the angular coordinates
Spherical coordinate system
In mathematics, a spherical coordinate system is a coordinate system for three-dimensional space where the position of a point is specified by three numbers: the radial distance of that point from a fixed origin, its inclination angle measured from a fixed zenith direction, and the azimuth angle of...
follows completely generally from this isotropy of the underlying potential: The eigenstates of the Hamiltonian
Hamiltonian (quantum mechanics)
In quantum mechanics, the Hamiltonian H, also Ȟ or Ĥ, is the operator corresponding to the total energy of the system. Its spectrum is the set of possible outcomes when one measures the total energy of a system...
(that is, the energy eigenstates) can be chosen as simultaneous eigenstates of the angular momentum operator
Angular momentum operator
In quantum mechanics, the angular momentum operator is an operator analogous to classical angular momentum. The angular momentum operator plays a central role in the theory of atomic physics and other quantum problems involving rotational symmetry...
. This corresponds to the fact that angular momentum is conserved in the orbital motion
Orbital motion (quantum)
Electrons don’t actually move in their orbitals. When quantum mechanics refer to “electron orbital motion” they are actually referring to the spatial wave function of the electron....
of the electron around the nucleus. Therefore, the energy eigenstates may be classified by two angular momentum quantum number
Quantum number
Quantum numbers describe values of conserved quantities in the dynamics of the quantum system. Perhaps the most peculiar aspect of quantum mechanics is the quantization of observable quantities. This is distinguished from classical mechanics where the values can range continuously...
s, ℓ and m (both are integers). The angular momentum quantum number determines the magnitude of the angular momentum. The magnetic quantum number determines the projection of the angular momentum on the (arbitrarily chosen) z-axis.
In addition to mathematical expressions for total angular momentum and angular momentum projection of wavefunctions, an expression for the radial dependence of the wave functions must be found. It is only here that the details of the 1/r Coulomb potential enter (leading to Laguerre polynomials
Laguerre polynomials
In mathematics, the Laguerre polynomials, named after Edmond Laguerre ,are the canonical solutions of Laguerre's equation:x\,y + \,y' + n\,y = 0\,which is a second-order linear differential equation....
in r). This leads to a third quantum number, the principal quantum number . The principal quantum number in hydrogen is related to atom's total energy.
Note that the maximum value of the angular momentum quantum number is limited by the principal quantum number: it can run only up to n − 1, i.e. .
Due to angular momentum conservation, states of the same ℓ but different m have the same energy (this holds for all problems with rotational symmetry
Rotational symmetry
Generally speaking, an object with rotational symmetry is an object that looks the same after a certain amount of rotation. An object may have more than one rotational symmetry; for instance, if reflections or turning it over are not counted, the triskelion appearing on the Isle of Man's flag has...
). In addition, for the hydrogen atom, states of the same n but different ℓ are also degenerate
Degenerate energy levels
In physics, two or more different quantum states are said to be degenerate if they are all at the same energy level. Statistically this means that they are all equally probable of being filled, and in Quantum Mechanics it is represented mathematically by the Hamiltonian for the system having more...
(i.e. they have the same energy). However, this is a specific property of hydrogen and is no longer true for more complicated atoms which have a (effective) potential differing from the form 1/r (due to the presence of the inner electrons shielding the nucleus potential).
Taking into account the spin
Spin (physics)
In quantum mechanics and particle physics, spin is a fundamental characteristic property of elementary particles, composite particles , and atomic nuclei.It is worth noting that the intrinsic property of subatomic particles called spin and discussed in this article, is related in some small ways,...
of the electron adds a last quantum number, the projection of the electron's spin angular momentum along the z-axis, which can take on two values. Therefore, any eigenstate of the electron in the hydrogen atom is described fully by four quantum numbers. According to the usual rules of quantum mechanics, the actual state of the electron may be any superposition
Quantum superposition
Quantum superposition is a fundamental principle of quantum mechanics. It holds that a physical system exists in all its particular, theoretically possible states simultaneously; but, when measured, it gives a result corresponding to only one of the possible configurations.Mathematically, it...
of these states. This explains also why the choice of z-axis for the directional quantization
Quantization (physics)
In physics, quantization is the process of explaining a classical understanding of physical phenomena in terms of a newer understanding known as "quantum mechanics". It is a procedure for constructing a quantum field theory starting from a classical field theory. This is a generalization of the...
of the angular momentum vector is immaterial: an orbital of given ℓ and m′ obtained for another preferred axis z′ can always be represented as a suitable superposition of the various states of different m (but same l) that have been obtained for z.
Alternatives to the Schrödinger Theory
In the language of Heisenberg's Matrix Mechanics, the hydrogen atom was first solved by Wolfgang PauliWolfgang Pauli
Wolfgang Ernst Pauli was an Austrian theoretical physicist and one of the pioneers of quantum physics. In 1945, after being nominated by Albert Einstein, he received the Nobel Prize in Physics for his "decisive contribution through his discovery of a new law of Nature, the exclusion principle or...
using a rotational symmetry in four dimension [O(4)-symmetry] generated by the angular momentum
and the Laplace–Runge–Lenz vector. By extending the symmetry group O(4) to the dynamical group O(4,2),
the entire spectrum and all transitions were embedded in a single irreducible group representation.
In 1979 the (non relativistic) hydrogen atom was solved for the first time within Feynman's path integral formulation
Path integral formulation
The path integral formulation of quantum mechanics is a description of quantum theory which generalizes the action principle of classical mechanics...
of quantum mechanics
Quantum mechanics
Quantum mechanics, also known as quantum physics or quantum theory, is a branch of physics providing a mathematical description of much of the dual particle-like and wave-like behavior and interactions of energy and matter. It departs from classical mechanics primarily at the atomic and subatomic...
. This work greatly extended the range of applicability of Feynman's method.
Energy levels
The energy levels of hydrogen, including fine structureFine structure
In atomic physics, the fine structure describes the splitting of the spectral lines of atoms due to first order relativistic corrections.The gross structure of line spectra is the line spectra predicted by non-relativistic electrons with no spin. For a hydrogenic atom, the gross structure energy...
, are given by
where α is the fine-structure constant
Fine-structure constant
In physics, the fine-structure constant is a fundamental physical constant, namely the coupling constant characterizing the strength of the electromagnetic interaction. Being a dimensionless quantity, it has constant numerical value in all systems of units...
and j is a number which is the total angular momentum eigenvalue; that is, depending on the direction of the electron spin. The quantity in square brackets arises from relativistic (spin-orbit) coupling interactions (as further described below in the section entitled "Features going beyond the Schrödinger solution").
The value of 13.6 eV is called the Rydberg constant
Rydberg constant
The Rydberg constant, symbol R∞, named after the Swedish physicist Johannes Rydberg, is a physical constant relating to atomic spectra in the science of spectroscopy. Rydberg initially determined its value empirically from spectroscopy, but Niels Bohr later showed that its value could be calculated...
and can be found from the Bohr model
Bohr model
In atomic physics, the Bohr model, introduced by Niels Bohr in 1913, depicts the atom as a small, positively charged nucleus surrounded by electrons that travel in circular orbits around the nucleus—similar in structure to the solar system, but with electrostatic forces providing attraction,...
, and is given by
where me is the mass of the electron, qe is the charge of the electron, h is the Planck constant
Planck constant
The Planck constant , also called Planck's constant, is a physical constant reflecting the sizes of energy quanta in quantum mechanics. It is named after Max Planck, one of the founders of quantum theory, who discovered it in 1899...
, and ε0 is the vacuum permittivity.
The Rydberg constant
Rydberg constant
The Rydberg constant, symbol R∞, named after the Swedish physicist Johannes Rydberg, is a physical constant relating to atomic spectra in the science of spectroscopy. Rydberg initially determined its value empirically from spectroscopy, but Niels Bohr later showed that its value could be calculated...
is connected to the fine-structure constant by the relation
This constant is often used in atomic physics
Atomic physics
Atomic physics is the field of physics that studies atoms as an isolated system of electrons and an atomic nucleus. It is primarily concerned with the arrangement of electrons around the nucleus and...
in the form of the Rydberg unit of energy:
The exact value of the Rydberg constant above assumes that the nucleus is infinitely massive with respect to the electron. For hydrogen-1, hydrogen-2 (deuterium
Deuterium
Deuterium, also called heavy hydrogen, is one of two stable isotopes of hydrogen. It has a natural abundance in Earth's oceans of about one atom in of hydrogen . Deuterium accounts for approximately 0.0156% of all naturally occurring hydrogen in Earth's oceans, while the most common isotope ...
), and hydrogen-3 (tritium
Tritium
Tritium is a radioactive isotope of hydrogen. The nucleus of tritium contains one proton and two neutrons, whereas the nucleus of protium contains one proton and no neutrons...
) the constant must be slight modified to use the reduced mass
Reduced mass
Reduced mass is the "effective" inertial mass appearing in the two-body problem of Newtonian mechanics. This is a quantity with the unit of mass, which allows the two-body problem to be solved as if it were a one-body problem. Note however that the mass determining the gravitational force is not...
of the system, rather than simply the mass of the electron. However, since the nucleus is much heavier than the electron, the values are nearly the same. The Rydberg constant RM for a hydrogen atom (one electron), R is given by :
where
is the rest mass of the electron, and M is the mass of the atomic nucleus. For hydrogen-1, the quantity 
is about 1/1836, reflecting the ratio electron to proton mass. For deuterium and tritium, the numbers are about 1/3670 and 1/5497 respectively. These figures, when added to 1 in the denominator, represent very small corrections in the value of R, and thus only small corrections to all energy levels in corresponding hydrogen isotopes.Wavefunction
The normalized position wavefunctionWavefunction
Not to be confused with the related concept of the Wave equationA wave function or wavefunction is a probability amplitude in quantum mechanics describing the quantum state of a particle and how it behaves. Typically, its values are complex numbers and, for a single particle, it is a function of...
s, given in spherical coordinates are:
where:
,
is the Bohr radiusBohr radius
The Bohr radius is a physical constant, approximately equal to the most probable distance between the proton and electron in a hydrogen atom in its ground state. It is named after Niels Bohr, due to its role in the Bohr model of an atom...
,
are the generalized Laguerre polynomials of degree , and
is a spherical harmonicSpherical Harmonic
Spherical Harmonic is a science fiction novel from the Saga of the Skolian Empire by Catherine Asaro. It tells the story of Dyhianna Selei , the Ruby Pharaoh of the Skolian Imperialate, as she strives to reform her government and reunite her family in the aftermath of a devastating interstellar...
function of degree ℓ and order m. Note that the generalized Laguerre polynomials are defined differently by different authors. The usage here is consistent with the definitions used by Messiah and Griffiths . But not Mathematica where it differs by a factor of
In other places, the Generalized Laguerre polynomial appearing in the Hydrogen wave function may be 
.The quantum numbers can take the following values:
Additionally, these wavefunctions are normalized (i.e., the integral of their modulus square equals 1) and orthogonal
Orthogonal functions
In mathematics, two functions f and g are called orthogonal if their inner product \langle f,g\rangle is zero for f ≠ g. Whether or not two particular functions are orthogonal depends on how their inner product has been defined. A typical definition of an inner product for functions is...
:
where
is the representation of the wavefunction 
in Dirac notation, and 
is the Kronecker delta function.Angular momentum
The eigenvalues for Angular momentum operatorAngular momentum operator
In quantum mechanics, the angular momentum operator is an operator analogous to classical angular momentum. The angular momentum operator plays a central role in the theory of atomic physics and other quantum problems involving rotational symmetry...
:
Visualizing the hydrogen electron orbitals
Probability amplitude
In quantum mechanics, a probability amplitude is a complex number whose modulus squared represents a probability or probability density.For example, if the probability amplitude of a quantum state is \alpha, the probability of measuring that state is |\alpha|^2...
that are color-coded (black represents zero density and white represents the highest density). The angular momentum (orbital) quantum number ℓ is denoted in each column, using the usual spectroscopic letter code (s means ℓ = 0, p means ℓ = 1, d means ℓ = 2). The main (principal) quantum number n (= 1, 2, 3, ...) is marked to the right of each row. For all pictures the magnetic quantum number m has been set to 0, and the cross-sectional plane is the xz-plane (z is the vertical axis). The probability density in three-dimensional space is obtained by rotating the one shown here around the z-axis.
The "ground state
Ground state
The ground state of a quantum mechanical system is its lowest-energy state; the energy of the ground state is known as the zero-point energy of the system. An excited state is any state with energy greater than the ground state...
", i.e. the state of lowest energy, in which the electron is usually found, is the first one, the 1s state (principal quantum level n = 1, ℓ = 0).