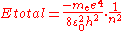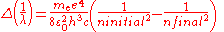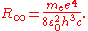Rydberg constant
Encyclopedia
The Rydberg constant, symbol R∞, named after the Swedish physicist
Johannes Rydberg
, is a physical constant
relating to atomic spectra
in the science of spectroscopy
. Rydberg initially determined its value empirically from spectroscopy, but Niels Bohr
later showed that its value could be calculated
from more fundamental constants by using quantum mechanics
. As of 2010, it is the most accurately measured fundamental physical constant.
The Rydberg constant represents the limiting value of the highest wavenumber
(the inverse wavelength) of any photon that can be emitted from the hydrogen atom, or, alternatively, the wavenumber of the lowest-energy photon capable of ionizing the hydrogen atom from its ground state. The spectrum of hydrogen can be expressed simply in terms of the Rydberg constant, using the Rydberg formula
.
The Rydberg unit of energy, symbol Ry, is closely related to the Rydberg constant. It corresponds to the energy of the photon whose wavenumber is the Rydberg constant, i.e. the ionization energy of the hydrogen atom.
of the nucleus, according to the 2010 CODATA the constant is:
where
is the rest mass of the electron
,
is the elementary charge
,
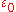is the permittivity of free space, 
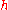is the Planck constant
, and
is the speed of light
in a vacuum.
This constant is often used in atomic physics
in the form of the Rydberg unit of energy: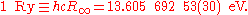
Two complications arise. One is that one may wish to discuss a hydrogen-like ion; that is, an atom with atomic number Z that has only one electron, such as C5+. In this case, the wavenumbers and photon energies are scaled up by a factor of Z2, neglecting relativistic effects. The other is that the mass of the atomic nucleus is not actually infinite compared to the mass of the electron. The predicted spectrum must then be corrected by substituting the reduced mass
for the mass of the electron. The Rydberg constant RM for an atom with one electron is then given by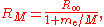
where
is the rest mass of the electron, and M is the mass of the atomic nucleus.
.
The Rydberg constant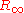
is defined by the spectrum that a hydrogen atom would have if its nucleus was infinitely massive, if there was no fine structure
or hyperfine splitting, and so on. Therefore it cannot be directly measured at very high accuracy from the atomic transition frequencies
of hydrogen alone. Instead, the Rydberg constant is inferred from measurements of atomic transition frequencies in three different atoms (hydrogen
, deuterium
, and antiprotonic helium
). Detailed theoretical calculations in the framework of quantum electrodynamics
are used to account for the effects of finite nuclear mass, fine structure, hyperfine splitting, and so on. Finally, the value of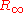
comes from the best fit of the measurements to the theory.
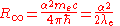
and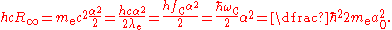
where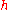
is the Planck constant
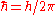is the reduced Planck constant,
is the speed of light
in a vacuum,
is the fine-structure constant
,
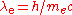is the Compton wavelength
of the electron,
is the Compton frequency of the electron,
is the Compton angular frequency of the electron,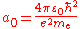
is the Bohr radius
.
The second equation is relevant because it is the coefficient for the energy of the atomic orbitals of a hydrogen atom:
.
was found empirically (experimentally), and it predated the development of quantum theory. To understand its significance in terms of the quantum theory, we can start from the equation
for the energy of an atom with one electron and a nucleus with a charge of +1 and an infinite mass. Of course, atomic nuclei do not have infinite masses in real life, but even the lightest nucleus, a single proton, is over 1800 times heavier than an electron, so this is reasonable as a first approximation. This energy formula can be derived either from the Bohr model
or from a fully quantum-mechanical treatment of a hydrogen-like atom
. Therefore the change in energy due to the electron changing from one value of
to another is
We simply change the units to wavenumbers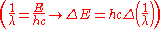
and we get
where
We have therefore found the Rydberg constant for our hypothetical system of a nucleus with infinite mass, a +1 charge, and a single electron to be
Physicist
A physicist is a scientist who studies or practices physics. Physicists study a wide range of physical phenomena in many branches of physics spanning all length scales: from sub-atomic particles of which all ordinary matter is made to the behavior of the material Universe as a whole...
Johannes Rydberg
Johannes Rydberg
Johannes Robert Rydberg, , , was a Swedish physicist mainly known for devising the Rydberg formula, in 1888, which is used to predict the wavelengths of photons emitted by changes in the energy level of an electron in a hydrogen atom.The physical constant known as the...
, is a physical constant
Physical constant
A physical constant is a physical quantity that is generally believed to be both universal in nature and constant in time. It can be contrasted with a mathematical constant, which is a fixed numerical value but does not directly involve any physical measurement.There are many physical constants in...
relating to atomic spectra
Spectrum
A spectrum is a condition that is not limited to a specific set of values but can vary infinitely within a continuum. The word saw its first scientific use within the field of optics to describe the rainbow of colors in visible light when separated using a prism; it has since been applied by...
in the science of spectroscopy
Spectroscopy
Spectroscopy is the study of the interaction between matter and radiated energy. Historically, spectroscopy originated through the study of visible light dispersed according to its wavelength, e.g., by a prism. Later the concept was expanded greatly to comprise any interaction with radiative...
. Rydberg initially determined its value empirically from spectroscopy, but Niels Bohr
Niels Bohr
Niels Henrik David Bohr was a Danish physicist who made foundational contributions to understanding atomic structure and quantum mechanics, for which he received the Nobel Prize in Physics in 1922. Bohr mentored and collaborated with many of the top physicists of the century at his institute in...
later showed that its value could be calculated
Bohr model
In atomic physics, the Bohr model, introduced by Niels Bohr in 1913, depicts the atom as a small, positively charged nucleus surrounded by electrons that travel in circular orbits around the nucleus—similar in structure to the solar system, but with electrostatic forces providing attraction,...
from more fundamental constants by using quantum mechanics
Quantum mechanics
Quantum mechanics, also known as quantum physics or quantum theory, is a branch of physics providing a mathematical description of much of the dual particle-like and wave-like behavior and interactions of energy and matter. It departs from classical mechanics primarily at the atomic and subatomic...
. As of 2010, it is the most accurately measured fundamental physical constant.
The Rydberg constant represents the limiting value of the highest wavenumber
Wavenumber
In the physical sciences, the wavenumber is a property of a wave, its spatial frequency, that is proportional to the reciprocal of the wavelength. It is also the magnitude of the wave vector...
(the inverse wavelength) of any photon that can be emitted from the hydrogen atom, or, alternatively, the wavenumber of the lowest-energy photon capable of ionizing the hydrogen atom from its ground state. The spectrum of hydrogen can be expressed simply in terms of the Rydberg constant, using the Rydberg formula
Rydberg formula
The Rydberg formula is used in atomic physics to describe the wavelengths of spectral lines of many chemical elements. It was formulated by the Swedish physicist Johannes Rydberg, and presented on November 5, 1888.-History:...
.
The Rydberg unit of energy, symbol Ry, is closely related to the Rydberg constant. It corresponds to the energy of the photon whose wavenumber is the Rydberg constant, i.e. the ionization energy of the hydrogen atom.
Value of the Rydberg constant and Rydberg unit of energy
Making use of the simplifying assumption that the mass of the atomic nucleus is infinite compared to the mass of the electron, so that the center of mass of the system lies at the barycenterCenter of mass
In physics, the center of mass or barycenter of a system is the average location of all of its mass. In the case of a rigid body, the position of the center of mass is fixed in relation to the body...
of the nucleus, according to the 2010 CODATA the constant is:
where
is the rest mass of the electronElectron
The electron is a subatomic particle with a negative elementary electric charge. It has no known components or substructure; in other words, it is generally thought to be an elementary particle. An electron has a mass that is approximately 1/1836 that of the proton...
,
is the elementary chargeElementary charge
The elementary charge, usually denoted as e, is the electric charge carried by a single proton, or equivalently, the absolute value of the electric charge carried by a single electron. This elementary charge is a fundamental physical constant. To avoid confusion over its sign, e is sometimes called...
,
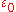is the permittivity of free space, 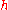is the Planck constantPlanck constant
The Planck constant , also called Planck's constant, is a physical constant reflecting the sizes of energy quanta in quantum mechanics. It is named after Max Planck, one of the founders of quantum theory, who discovered it in 1899...
, and
is the speed of lightSpeed of light
The speed of light in vacuum, usually denoted by c, is a physical constant important in many areas of physics. Its value is 299,792,458 metres per second, a figure that is exact since the length of the metre is defined from this constant and the international standard for time...
in a vacuum.
This constant is often used in atomic physics
Atomic physics
Atomic physics is the field of physics that studies atoms as an isolated system of electrons and an atomic nucleus. It is primarily concerned with the arrangement of electrons around the nucleus and...
in the form of the Rydberg unit of energy:
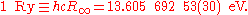
Two complications arise. One is that one may wish to discuss a hydrogen-like ion; that is, an atom with atomic number Z that has only one electron, such as C5+. In this case, the wavenumbers and photon energies are scaled up by a factor of Z2, neglecting relativistic effects. The other is that the mass of the atomic nucleus is not actually infinite compared to the mass of the electron. The predicted spectrum must then be corrected by substituting the reduced mass
Reduced mass
Reduced mass is the "effective" inertial mass appearing in the two-body problem of Newtonian mechanics. This is a quantity with the unit of mass, which allows the two-body problem to be solved as if it were a one-body problem. Note however that the mass determining the gravitational force is not...
for the mass of the electron. The Rydberg constant RM for an atom with one electron is then given by
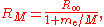
where
is the rest mass of the electron, and M is the mass of the atomic nucleus.Measurement
The Rydberg constant is the most well-determined physical constant, with a relative experimental uncertainty of less than 7 parts in 1012. The ability to measure it to such a high precision constrains the proportions of the values of the other physical constants that define it. See precision tests of QEDPrecision tests of QED
Quantum electrodynamics , a relativistic quantum field theory of electrodynamics, is among the most stringently tested theories in physics....
.
The Rydberg constant
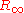is defined by the spectrum that a hydrogen atom would have if its nucleus was infinitely massive, if there was no fine structureFine structure
In atomic physics, the fine structure describes the splitting of the spectral lines of atoms due to first order relativistic corrections.The gross structure of line spectra is the line spectra predicted by non-relativistic electrons with no spin. For a hydrogenic atom, the gross structure energy...
or hyperfine splitting, and so on. Therefore it cannot be directly measured at very high accuracy from the atomic transition frequencies
Atomic spectral line
In physics, atomic spectral lines are of two types:* An emission line is formed when an electron makes a transition from a particular discrete energy level of an atom, to a lower energy state, emitting a photon of a particular energy and wavelength...
of hydrogen alone. Instead, the Rydberg constant is inferred from measurements of atomic transition frequencies in three different atoms (hydrogen
Hydrogen
Hydrogen is the chemical element with atomic number 1. It is represented by the symbol H. With an average atomic weight of , hydrogen is the lightest and most abundant chemical element, constituting roughly 75% of the Universe's chemical elemental mass. Stars in the main sequence are mainly...
, deuterium
Deuterium
Deuterium, also called heavy hydrogen, is one of two stable isotopes of hydrogen. It has a natural abundance in Earth's oceans of about one atom in of hydrogen . Deuterium accounts for approximately 0.0156% of all naturally occurring hydrogen in Earth's oceans, while the most common isotope ...
, and antiprotonic helium
Antiprotonic helium
Antiprotonic helium is a three-body atom composed of an antiproton and an electron orbiting around a helium nucleus. It is thus made partly of matter, and partly of antimatter. The atom is electrically neutral, since both electrons and antiprotons have a charge of -1, whereas helium nuclei have a...
). Detailed theoretical calculations in the framework of quantum electrodynamics
Quantum electrodynamics
Quantum electrodynamics is the relativistic quantum field theory of electrodynamics. In essence, it describes how light and matter interact and is the first theory where full agreement between quantum mechanics and special relativity is achieved...
are used to account for the effects of finite nuclear mass, fine structure, hyperfine splitting, and so on. Finally, the value of
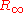comes from the best fit of the measurements to the theory.Alternative expressions
The Rydberg constant can also be expressed as the following equations.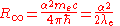and
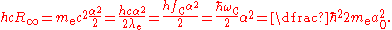
where
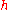is the Planck constantPlanck constant
The Planck constant , also called Planck's constant, is a physical constant reflecting the sizes of energy quanta in quantum mechanics. It is named after Max Planck, one of the founders of quantum theory, who discovered it in 1899...
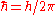is the reduced Planck constant, is the speed of lightSpeed of light
The speed of light in vacuum, usually denoted by c, is a physical constant important in many areas of physics. Its value is 299,792,458 metres per second, a figure that is exact since the length of the metre is defined from this constant and the international standard for time...
in a vacuum,
is the fine-structure constantFine-structure constant
In physics, the fine-structure constant is a fundamental physical constant, namely the coupling constant characterizing the strength of the electromagnetic interaction. Being a dimensionless quantity, it has constant numerical value in all systems of units...
,
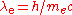is the Compton wavelengthCompton wavelength
The Compton wavelength is a quantum mechanical property of a particle. It was introduced by Arthur Compton in his explanation of the scattering of photons by electrons...
of the electron,
is the Compton frequency of the electron, is the Compton angular frequency of the electron,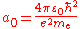 is the Bohr radiusBohr radius
The Bohr radius is a physical constant, approximately equal to the most probable distance between the proton and electron in a hydrogen atom in its ground state. It is named after Niels Bohr, due to its role in the Bohr model of an atom...
.
The second equation is relevant because it is the coefficient for the energy of the atomic orbitals of a hydrogen atom:
.The derivation of Rydberg constant from quantum mechanics
Historically, the Rydberg formulaRydberg formula
The Rydberg formula is used in atomic physics to describe the wavelengths of spectral lines of many chemical elements. It was formulated by the Swedish physicist Johannes Rydberg, and presented on November 5, 1888.-History:...
was found empirically (experimentally), and it predated the development of quantum theory. To understand its significance in terms of the quantum theory, we can start from the equation
for the energy of an atom with one electron and a nucleus with a charge of +1 and an infinite mass. Of course, atomic nuclei do not have infinite masses in real life, but even the lightest nucleus, a single proton, is over 1800 times heavier than an electron, so this is reasonable as a first approximation. This energy formula can be derived either from the Bohr model
Bohr model
In atomic physics, the Bohr model, introduced by Niels Bohr in 1913, depicts the atom as a small, positively charged nucleus surrounded by electrons that travel in circular orbits around the nucleus—similar in structure to the solar system, but with electrostatic forces providing attraction,...
or from a fully quantum-mechanical treatment of a hydrogen-like atom
Hydrogen-like atom
A hydrogen-like ion is any atomic nucleus with one electron and thus is isoelectronic with hydrogen. Except for the hydrogen atom itself , these ions carry the positive charge e, where Z is the atomic number of the atom. Examples of hydrogen-like ions are He+, Li2+, Be3+ and B4+...
. Therefore the change in energy due to the electron changing from one value of
to another is
We simply change the units to wavenumbers
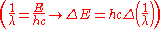and we get
where
-
-
is Planck's constant, -
is the rest mass of the electronElectronThe electron is a subatomic particle with a negative elementary electric charge. It has no known components or substructure; in other words, it is generally thought to be an elementary particle. An electron has a mass that is approximately 1/1836 that of the proton...
, -
is the elementary chargeElementary chargeThe elementary charge, usually denoted as e, is the electric charge carried by a single proton, or equivalently, the absolute value of the electric charge carried by a single electron. This elementary charge is a fundamental physical constant. To avoid confusion over its sign, e is sometimes called...
, -
is the speed of lightSpeed of lightThe speed of light in vacuum, usually denoted by c, is a physical constant important in many areas of physics. Its value is 299,792,458 metres per second, a figure that is exact since the length of the metre is defined from this constant and the international standard for time...
in vacuumVacuumIn everyday usage, vacuum is a volume of space that is essentially empty of matter, such that its gaseous pressure is much less than atmospheric pressure. The word comes from the Latin term for "empty". A perfect vacuum would be one with no particles in it at all, which is impossible to achieve in...
, and -
is the permittivity of free space. -
and 
being the electron shell number of the hydrogen atom.
-
We have therefore found the Rydberg constant for our hypothetical system of a nucleus with infinite mass, a +1 charge, and a single electron to be
