Precision tests of QED
Encyclopedia
Quantum electrodynamics
(QED), a relativistic quantum field theory of electrodynamics, is among the most stringently tested theories in physics
.
Precision tests of QED consist of measurements of the electromagnetic fine structure constant, α, in different physical systems. Checking the consistency of such measurements tests the theory.
Tests of a theory are normally carried out by comparing experimental results to theoretical predictions. In QED, there is some subtlety in this comparison, because theoretical predictions require as input an extremely precise value of α, which can only be obtained from another precision QED experiment. Because of this, the comparisons between theory and experiment are usually quoted as independent determinations of α. QED is then confirmed to the extent that these measurements of α from different physical sources agree with each other.
The agreement found this way is to within ten parts in a billion (10−8), based on the comparison of the electron
anomalous magnetic dipole moment
and the Rydberg constant
from atom recoil measurements as described below. This makes QED one of the most accurate physical theories constructed thus far.
experiments, high-energy collider
experiments, and condensed matter
systems. The value of α is obtained in each of these experiments by fitting an experimental measurement to a theoretical expression (including higher-order radiative corrections
) that includes α as a parameter. The uncertainty in the extracted value of α includes both experimental and theoretical uncertainties. This program thus requires both high-precision measurements and high-precision theoretical calculations. Unless noted otherwise, all results below are taken from .
, or g−2 ("g minus 2"), of the electron
. To make this measurement, two ingredients are needed:
As of February 2007, the best measurement of the anomalous magnetic dipole moment of the electron was made by Gabrielse et al. using a single electron caught in a Penning trap
. The difference between the electron's cyclotron frequency and its spin precession frequency in a magnetic field is proportional to g−2. An extremely high precision measurement of the quantized energies of the cyclotron orbits, or Landau levels, of the electron, compared to the quantized energies of the electron's two possible spin
orientations, gives a value for the electron's spin g-factor:
a precision of better than one part in a trillion. (The digits in parentheses indicate the uncertainty in the last listed digits of the measurement.)
The current state-of-the-art theoretical calculation of the anomalous magnetic dipole moment of the electron includes QED diagrams with up to four loops. Combining this with the experimental measurement of g yields the most precise value of α:
a precision of better than a part in a billion. This uncertainty is ten times smaller than the nearest rival method involving atom-recoil measurements.
A value of α can also be extracted from the anomalous magnetic dipole moment of the muon
. The g-factor of the muon is extracted using the same physical principle as for the electron above – namely, that the difference between the cyclotron frequency and the spin precession frequency in a magnetic field is proportional to g−2. The most precise measurement comes from Brookhaven National Laboratory
's muon g−2 experiment, in which polarized muons are stored in a cyclotron and their spin orientation is measured by the direction of their decay electrons. As of February 2007, the current world average muon g-factor measurement is,
a precision of better than one part in a billion. The difference between the g-factors of the muon and the electron is due to their difference in mass. Because of the muon's larger mass, contributions to the theoretical calculation of its anomalous magnetic dipole moment from Standard Model
weak interactions and from contributions involving hadrons are important at the current level of precision, whereas these effects are not important for the electron. The muon's anomalous magnetic dipole moment is also sensitive to contributions from new physics beyond the Standard Model
, such as supersymmetry
. For this reason, the muon's anomalous magnetic moment is normally used as a probe for new physics beyond the Standard Model rather than as a test of QED.
. The Rydberg constant is known to seven parts in a trillion. The mass of the electron relative to that of caesium
and rubidium
atoms is also known with extremely high precision. If the mass of the electron can be gotten with high enough precision, then α can be found from the Rydberg constant according to
.
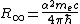To get the mass of the electron, this method actually measures the mass of an 87Rb
atom by measuring the recoil speed of the atom after it emits a photon of known wavelength in an atomic transition. Combining this with the ratio of electron to 87Rb atom, the result for α is,
Because this measurement is the next-most-precise after the measurement of α from the electron's anomalous magnetic dipole moment described above, their comparison provides the most stringent test of QED, which is passed with flying colors: the value of α obtained here is within one standard deviation of that found from the electron's anomalous magnetic dipole moment, an agreement to within ten parts in a billion.
is used. The neutron mass is measured with high precision through a very precise measurement of its Compton wavelength
. This is then combined with the value of the Rydberg constant to extract α. The result is,
caused by the interaction between the magnetic moment
of the nucleus
and the combined spin
and orbital magnetic moment of the electron. The hyperfine splitting in hydrogen
, measured using Ramsey's hydrogen maser
, is the most precisely known quantity in physics. Unfortunately, the influence of the proton
's internal structure limits how precisely the splitting can be predicted theoretically. This leads to the extracted value of α being dominated by theoretical uncertainty:
The hyperfine splitting in muonium
, an "atom" consisting of an electron and an antimuon, provides a more precise measurement of α because the muon has no internal structure:
, which arises from a one-loop effect in quantum electrodynamics. The Lamb shift is proportional to α5 and its measurement yields the extracted value:
is an "atom" consisting of an electron and a positron
. Whereas the calculation of the energy levels of ordinary hydrogen is contaminated by theoretical uncertainties from the proton's internal structure, the particles that make up positronium have no internal structure so precise theoretical calculations can be performed. The measurement of the splitting between the 2 3S1 and the 1 3S1 energy levels of positronium yields
Measurements of α can also be extracted from the positronium decay rate. Positronium decays through the annihilation of the electron and the positron into two or more gamma-ray photons. The decay rate of the singlet ("para-positronium") 1S0 state yields
and the decay rate of the triplet ("ortho-positronium") 3S1 state yields
This last result is the only serious discrepancy among the numbers given here, but there is some evidence that uncalculated higher-order quantum corrections give a large correction to the value quoted here.
of higher-order QED reactions at high-energy electron-positron colliders provide a determination of α. In order to compare the extracted value of α with the low-energy results, higher-order QED effects including the running of α due to vacuum polarization
must be taken into account. These experiments typically achieve only percent-level accuracy, but their results are consistent with the precise measurements available at lower energies.
The cross section for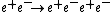
yields
and the cross section for
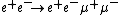yields
Josephson effect
are exotic quantum interference phenomena in condensed matter systems. These two effects provide a standard electrical resistance
and a standard frequency
, respectively, which are believed to measure the charge of the electron with corrections that are strictly zero for macroscopic systems.
The quantum Hall effect yields
and the AC Josephson effect yields
Quantum electrodynamics
Quantum electrodynamics is the relativistic quantum field theory of electrodynamics. In essence, it describes how light and matter interact and is the first theory where full agreement between quantum mechanics and special relativity is achieved...
(QED), a relativistic quantum field theory of electrodynamics, is among the most stringently tested theories in physics
Physics
Physics is a natural science that involves the study of matter and its motion through spacetime, along with related concepts such as energy and force. More broadly, it is the general analysis of nature, conducted in order to understand how the universe behaves.Physics is one of the oldest academic...
.
Precision tests of QED consist of measurements of the electromagnetic fine structure constant, α, in different physical systems. Checking the consistency of such measurements tests the theory.
Tests of a theory are normally carried out by comparing experimental results to theoretical predictions. In QED, there is some subtlety in this comparison, because theoretical predictions require as input an extremely precise value of α, which can only be obtained from another precision QED experiment. Because of this, the comparisons between theory and experiment are usually quoted as independent determinations of α. QED is then confirmed to the extent that these measurements of α from different physical sources agree with each other.
The agreement found this way is to within ten parts in a billion (10−8), based on the comparison of the electron
Electron
The electron is a subatomic particle with a negative elementary electric charge. It has no known components or substructure; in other words, it is generally thought to be an elementary particle. An electron has a mass that is approximately 1/1836 that of the proton...
anomalous magnetic dipole moment
Anomalous magnetic dipole moment
In quantum electrodynamics, the anomalous magnetic moment of a particle is a contribution of effects of quantum mechanics, expressed by Feynman diagrams with loops, to the magnetic moment of that particle...
and the Rydberg constant
Rydberg constant
The Rydberg constant, symbol R∞, named after the Swedish physicist Johannes Rydberg, is a physical constant relating to atomic spectra in the science of spectroscopy. Rydberg initially determined its value empirically from spectroscopy, but Niels Bohr later showed that its value could be calculated...
from atom recoil measurements as described below. This makes QED one of the most accurate physical theories constructed thus far.
Precision QED experiments
Precision tests of QED have been performed in low-energy atomic physicsAtomic physics
Atomic physics is the field of physics that studies atoms as an isolated system of electrons and an atomic nucleus. It is primarily concerned with the arrangement of electrons around the nucleus and...
experiments, high-energy collider
Collider
A collider is a type of a particle accelerator involving directed beams of particles.Colliders may either be ring accelerators or linear accelerators.-Explanation:...
experiments, and condensed matter
Condensed Matter
Condensed matter may refer to several things*Condensed matter physics, the study of the physical properties of condensed phases of matter*European Physical Journal B: Condensed Matter and Complex Systems, a scientific journal published by EDP sciences...
systems. The value of α is obtained in each of these experiments by fitting an experimental measurement to a theoretical expression (including higher-order radiative corrections
Renormalization
In quantum field theory, the statistical mechanics of fields, and the theory of self-similar geometric structures, renormalization is any of a collection of techniques used to treat infinities arising in calculated quantities....
) that includes α as a parameter. The uncertainty in the extracted value of α includes both experimental and theoretical uncertainties. This program thus requires both high-precision measurements and high-precision theoretical calculations. Unless noted otherwise, all results below are taken from .
Anomalous magnetic dipole moments
The most precise measurement of α comes from the anomalous magnetic dipole momentAnomalous magnetic dipole moment
In quantum electrodynamics, the anomalous magnetic moment of a particle is a contribution of effects of quantum mechanics, expressed by Feynman diagrams with loops, to the magnetic moment of that particle...
, or g−2 ("g minus 2"), of the electron
Electron
The electron is a subatomic particle with a negative elementary electric charge. It has no known components or substructure; in other words, it is generally thought to be an elementary particle. An electron has a mass that is approximately 1/1836 that of the proton...
. To make this measurement, two ingredients are needed:
- 1) A precise measurement of the anomalous magnetic dipole moment, and
- 2) A precise theoretical calculation of the anomalous magnetic dipole moment in terms of α.
As of February 2007, the best measurement of the anomalous magnetic dipole moment of the electron was made by Gabrielse et al. using a single electron caught in a Penning trap
Penning trap
Penning traps are devices for the storage of charged particles using a homogeneous static magnetic field and a spatially inhomogeneous static electric field. This kind of trap is particularly well suited to precision measurements of properties of ions and stable subatomic particles which have...
. The difference between the electron's cyclotron frequency and its spin precession frequency in a magnetic field is proportional to g−2. An extremely high precision measurement of the quantized energies of the cyclotron orbits, or Landau levels, of the electron, compared to the quantized energies of the electron's two possible spin
Spin (physics)
In quantum mechanics and particle physics, spin is a fundamental characteristic property of elementary particles, composite particles , and atomic nuclei.It is worth noting that the intrinsic property of subatomic particles called spin and discussed in this article, is related in some small ways,...
orientations, gives a value for the electron's spin g-factor:
- g/2 = 1.001 159 652 180 85 (76),
a precision of better than one part in a trillion. (The digits in parentheses indicate the uncertainty in the last listed digits of the measurement.)
The current state-of-the-art theoretical calculation of the anomalous magnetic dipole moment of the electron includes QED diagrams with up to four loops. Combining this with the experimental measurement of g yields the most precise value of α:
- α−1 = 137.035 999 070 (98),
a precision of better than a part in a billion. This uncertainty is ten times smaller than the nearest rival method involving atom-recoil measurements.
A value of α can also be extracted from the anomalous magnetic dipole moment of the muon
Muon
The muon |mu]] used to represent it) is an elementary particle similar to the electron, with a unitary negative electric charge and a spin of ½. Together with the electron, the tau, and the three neutrinos, it is classified as a lepton...
. The g-factor of the muon is extracted using the same physical principle as for the electron above – namely, that the difference between the cyclotron frequency and the spin precession frequency in a magnetic field is proportional to g−2. The most precise measurement comes from Brookhaven National Laboratory
Brookhaven National Laboratory
Brookhaven National Laboratory , is a United States national laboratory located in Upton, New York on Long Island, and was formally established in 1947 at the site of Camp Upton, a former U.S. Army base...
's muon g−2 experiment, in which polarized muons are stored in a cyclotron and their spin orientation is measured by the direction of their decay electrons. As of February 2007, the current world average muon g-factor measurement is,
- g/2 = 1.001 165 920 8 (6),
a precision of better than one part in a billion. The difference between the g-factors of the muon and the electron is due to their difference in mass. Because of the muon's larger mass, contributions to the theoretical calculation of its anomalous magnetic dipole moment from Standard Model
Standard Model
The Standard Model of particle physics is a theory concerning the electromagnetic, weak, and strong nuclear interactions, which mediate the dynamics of the known subatomic particles. Developed throughout the mid to late 20th century, the current formulation was finalized in the mid 1970s upon...
weak interactions and from contributions involving hadrons are important at the current level of precision, whereas these effects are not important for the electron. The muon's anomalous magnetic dipole moment is also sensitive to contributions from new physics beyond the Standard Model
Beyond the Standard Model
Physics beyond the Standard Model refers to the theoretical developments needed to explain the deficiencies of the Standard Model, such as the origin of mass, the strong CP problem, neutrino oscillations, matter–antimatter asymmetry, and the nature of dark matter and dark energy...
, such as supersymmetry
Supersymmetry
In particle physics, supersymmetry is a symmetry that relates elementary particles of one spin to other particles that differ by half a unit of spin and are known as superpartners...
. For this reason, the muon's anomalous magnetic moment is normally used as a probe for new physics beyond the Standard Model rather than as a test of QED.
Atom-recoil measurements
This is an indirect method of measuring α, based on measurements of the masses of the electron, certain atoms, and the Rydberg constantRydberg constant
The Rydberg constant, symbol R∞, named after the Swedish physicist Johannes Rydberg, is a physical constant relating to atomic spectra in the science of spectroscopy. Rydberg initially determined its value empirically from spectroscopy, but Niels Bohr later showed that its value could be calculated...
. The Rydberg constant is known to seven parts in a trillion. The mass of the electron relative to that of caesium
Caesium
Caesium or cesium is the chemical element with the symbol Cs and atomic number 55. It is a soft, silvery-gold alkali metal with a melting point of 28 °C , which makes it one of only five elemental metals that are liquid at room temperature...
and rubidium
Rubidium
Rubidium is a chemical element with the symbol Rb and atomic number 37. Rubidium is a soft, silvery-white metallic element of the alkali metal group. Its atomic mass is 85.4678. Elemental rubidium is highly reactive, with properties similar to those of other elements in group 1, such as very rapid...
atoms is also known with extremely high precision. If the mass of the electron can be gotten with high enough precision, then α can be found from the Rydberg constant according to
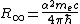.To get the mass of the electron, this method actually measures the mass of an 87Rb
Rubidium
Rubidium is a chemical element with the symbol Rb and atomic number 37. Rubidium is a soft, silvery-white metallic element of the alkali metal group. Its atomic mass is 85.4678. Elemental rubidium is highly reactive, with properties similar to those of other elements in group 1, such as very rapid...
atom by measuring the recoil speed of the atom after it emits a photon of known wavelength in an atomic transition. Combining this with the ratio of electron to 87Rb atom, the result for α is,
- α−1 = 137.035 998 78 (91).
Because this measurement is the next-most-precise after the measurement of α from the electron's anomalous magnetic dipole moment described above, their comparison provides the most stringent test of QED, which is passed with flying colors: the value of α obtained here is within one standard deviation of that found from the electron's anomalous magnetic dipole moment, an agreement to within ten parts in a billion.
Neutron Compton wavelength
This method of measuring α is very similar in principle to the atom-recoil method. In this case, the accurately known mass ratio of the electron to the neutronNeutron
The neutron is a subatomic hadron particle which has the symbol or , no net electric charge and a mass slightly larger than that of a proton. With the exception of hydrogen, nuclei of atoms consist of protons and neutrons, which are therefore collectively referred to as nucleons. The number of...
is used. The neutron mass is measured with high precision through a very precise measurement of its Compton wavelength
Compton wavelength
The Compton wavelength is a quantum mechanical property of a particle. It was introduced by Arthur Compton in his explanation of the scattering of photons by electrons...
. This is then combined with the value of the Rydberg constant to extract α. The result is,
- α−1 = 137.036 010 1 (5 4).
Hyperfine splitting
Hyperfine splitting is a splitting in the energy levels of an atomAtom
The atom is a basic unit of matter that consists of a dense central nucleus surrounded by a cloud of negatively charged electrons. The atomic nucleus contains a mix of positively charged protons and electrically neutral neutrons...
caused by the interaction between the magnetic moment
Magnetic moment
The magnetic moment of a magnet is a quantity that determines the force that the magnet can exert on electric currents and the torque that a magnetic field will exert on it...
of the nucleus
Atomic nucleus
The nucleus is the very dense region consisting of protons and neutrons at the center of an atom. It was discovered in 1911, as a result of Ernest Rutherford's interpretation of the famous 1909 Rutherford experiment performed by Hans Geiger and Ernest Marsden, under the direction of Rutherford. The...
and the combined spin
Spin (physics)
In quantum mechanics and particle physics, spin is a fundamental characteristic property of elementary particles, composite particles , and atomic nuclei.It is worth noting that the intrinsic property of subatomic particles called spin and discussed in this article, is related in some small ways,...
and orbital magnetic moment of the electron. The hyperfine splitting in hydrogen
Hydrogen
Hydrogen is the chemical element with atomic number 1. It is represented by the symbol H. With an average atomic weight of , hydrogen is the lightest and most abundant chemical element, constituting roughly 75% of the Universe's chemical elemental mass. Stars in the main sequence are mainly...
, measured using Ramsey's hydrogen maser
Maser
A maser is a device that produces coherent electromagnetic waves through amplification by stimulated emission. Historically, “maser” derives from the original, upper-case acronym MASER, which stands for "Microwave Amplification by Stimulated Emission of Radiation"...
, is the most precisely known quantity in physics. Unfortunately, the influence of the proton
Proton
The proton is a subatomic particle with the symbol or and a positive electric charge of 1 elementary charge. One or more protons are present in the nucleus of each atom, along with neutrons. The number of protons in each atom is its atomic number....
's internal structure limits how precisely the splitting can be predicted theoretically. This leads to the extracted value of α being dominated by theoretical uncertainty:
- α−1 = 137.036 0 (3).
The hyperfine splitting in muonium
Muonium
Muonium is an exotic atom made up of an antimuon and an electron, which was discovered in 1960 and is given the chemical symbol . During the muon's lifetime, muonium can enter into compounds such as muonium chloride or sodium muonide . Due to the mass difference between the antimuon and the...
, an "atom" consisting of an electron and an antimuon, provides a more precise measurement of α because the muon has no internal structure:
- α−1 = 137.035 994 (18).
Lamb shift
The Lamb shift is a small difference in the energies of the 2 S1/2 and 2 P1/2 energy levels of hydrogenHydrogen atom
A hydrogen atom is an atom of the chemical element hydrogen. The electrically neutral atom contains a single positively-charged proton and a single negatively-charged electron bound to the nucleus by the Coulomb force...
, which arises from a one-loop effect in quantum electrodynamics. The Lamb shift is proportional to α5 and its measurement yields the extracted value:
- α−1 = 137.036 8 (7).
Positronium
PositroniumPositronium
Positronium is a system consisting of an electron and its anti-particle, a positron, bound together into an "exotic atom". Being unstable, the two particles annihilate each other to produce two gamma ray photons after an average lifetime of 125 ps or three gamma ray photons after 142 ns in...
is an "atom" consisting of an electron and a positron
Positron
The positron or antielectron is the antiparticle or the antimatter counterpart of the electron. The positron has an electric charge of +1e, a spin of ½, and has the same mass as an electron...
. Whereas the calculation of the energy levels of ordinary hydrogen is contaminated by theoretical uncertainties from the proton's internal structure, the particles that make up positronium have no internal structure so precise theoretical calculations can be performed. The measurement of the splitting between the 2 3S1 and the 1 3S1 energy levels of positronium yields
- α−1 = 137.034 (16).
Measurements of α can also be extracted from the positronium decay rate. Positronium decays through the annihilation of the electron and the positron into two or more gamma-ray photons. The decay rate of the singlet ("para-positronium") 1S0 state yields
- α−1 = 137.00 (6),
and the decay rate of the triplet ("ortho-positronium") 3S1 state yields
- α−1 = 136.971 (6).
This last result is the only serious discrepancy among the numbers given here, but there is some evidence that uncalculated higher-order quantum corrections give a large correction to the value quoted here.
High-energy QED processes
The cross sectionsCross section (physics)
A cross section is the effective area which governs the probability of some scattering or absorption event. Together with particle density and path length, it can be used to predict the total scattering probability via the Beer-Lambert law....
of higher-order QED reactions at high-energy electron-positron colliders provide a determination of α. In order to compare the extracted value of α with the low-energy results, higher-order QED effects including the running of α due to vacuum polarization
Vacuum polarization
In quantum field theory, and specifically quantum electrodynamics, vacuum polarization describes a process in which a background electromagnetic field produces virtual electron–positron pairs that change the distribution of charges and currents that generated the original electromagnetic...
must be taken into account. These experiments typically achieve only percent-level accuracy, but their results are consistent with the precise measurements available at lower energies.
The cross section for
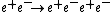yields- α−1 = 136.5 (2.7),
and the cross section for
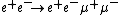yields- α−1 = 139.9 (1.2).
Condensed matter systems
The quantum Hall effect and the ACAlternating current
In alternating current the movement of electric charge periodically reverses direction. In direct current , the flow of electric charge is only in one direction....
Josephson effect
Josephson effect
The Josephson effect is the phenomenon of supercurrent across two superconductors coupled by a weak link...
are exotic quantum interference phenomena in condensed matter systems. These two effects provide a standard electrical resistance
Electrical resistance
The electrical resistance of an electrical element is the opposition to the passage of an electric current through that element; the inverse quantity is electrical conductance, the ease at which an electric current passes. Electrical resistance shares some conceptual parallels with the mechanical...
and a standard frequency
Frequency
Frequency is the number of occurrences of a repeating event per unit time. It is also referred to as temporal frequency.The period is the duration of one cycle in a repeating event, so the period is the reciprocal of the frequency...
, respectively, which are believed to measure the charge of the electron with corrections that are strictly zero for macroscopic systems.
The quantum Hall effect yields
- α−1 = 137.035 997 9 (3 2),
and the AC Josephson effect yields
- α−1 = 137.035 977 0 (7 7).