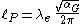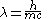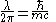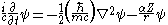Compton wavelength
Encyclopedia
The Compton wavelength is a quantum mechanical
property of a particle. It was introduced by Arthur Compton
in his explanation of the scattering of photon
s by electron
s (a process known as Compton scattering
). The Compton wavelength of a particle is equivalent to the wavelength
of a photon whose energy is the same as the rest-mass energy of the particle.
The Compton wavelength, λ, of a particle is given by
where h is the Planck constant
, m is the particle's rest mass
, and c is the speed of light
. The significance of this formula is shown in the derivation of the Compton shift formula.
The CODATA 2006 value for the Compton wavelength of the electron is . Other particles have different Compton wavelengths.
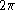, one obtains a smaller or “reduced” Compton wavelength:
The reduced Compton wavelength is a natural representation for mass on the quantum scale, and as such, it appears in many of the fundamental equations of quantum mechanics. The reduced Compton wavelength appears in the relativistic Klein–Gordon equation for a free particle:
It appears in the Dirac equation
(the following is an explicitly covariant form employing the Einstein summation convention
):
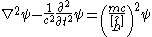
The reduced Compton wavelength also appears in Schrödinger's equation, although its presence is obscured in traditional representations of the equation. The following is the traditional representation of Schrödinger's equation for an electron in a hydrogen-like atom
:
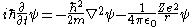
Dividing through by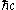
, and rewriting in terms of the fine structure constant, one obtains:
A particle of rest mass m has a rest energy of .
The non-reduced Compton wavelength for this particle is the wavelength of a photon of the same energy. For photons of frequency
f, energy is given by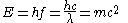
which yields the non-reduced Compton wavelength formula if solved for λ.
and special relativity
into account.
This depends on the mass m of the particle.
To see this, note that we can measure the position of a particle
by bouncing light off it - but measuring the position accurately requires light of short wavelength. Light with a short wavelength consists of photons of high energy. If the energy of these photons exceeds mc2, when one hits the particle whose position is being measured the collision may have enough energy to create a new particle of the same type. This
renders moot the question of the original particle's location.
This argument also shows that the reduced Compton wavelength is the cutoff below which quantum field theory
– which can describe particle creation and annihilation – becomes important.
We can make the above argument a bit more precise as follows. Suppose we wish to measure the position of a particle to within an accuracy Δx.
Then the uncertainty relation
for position and momentum
says that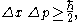
so the uncertainty in the particle's momentum satisfies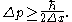
Using the relativistic relation between momentum and energy , when Δp exceeds mc then the uncertainty in energy is greater than mc2, which is enough energy
to create another particle of the same type. It follows that there is a fundamental limitation on Δx: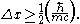
Thus the uncertainty in position must be greater than half of the reduced Compton wavelength ħ/mc.
The Compton wavelength can be contrasted with the de Broglie wavelength, which depends on the momentum of a particle and determines the cutoff between particle and wave behavior in quantum mechanics
.
)
The Bohr radius
is related to the Compton wavelength by:
= 
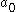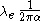
The classical electron radius
is written:
= 
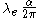
The Rydberg constant
is written:
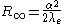
For fermion
s, the non-reduced Compton wavelength sets the cross-section of interactions. For example, the cross-section for Thomson scattering
of a photon from an electron is equal to
,
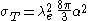For gauge
boson
s, the Compton wavelength sets the effective range of the Yukawa interaction
: since the photon
has no rest mass, electromagnetism has infinite range.
Typical lengths and areas in gravitational physics can be related to the Compton wavelength and the gravitational coupling constant
(
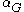which is the gravitational analog of the fine structure constant):
The Planck mass is special because the reduced Compton wavelength for this mass is equal to half of the Schwarzschild radius
. This special distance is called the Planck length (
). This is a simple case of dimensional analysis
: the Schwarzschild radius is proportional to the mass, whereas the Compton wavelength is proportional to the inverse of the mass. The Planck length is written:
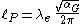
Quantum mechanics
Quantum mechanics, also known as quantum physics or quantum theory, is a branch of physics providing a mathematical description of much of the dual particle-like and wave-like behavior and interactions of energy and matter. It departs from classical mechanics primarily at the atomic and subatomic...
property of a particle. It was introduced by Arthur Compton
Arthur Compton
Arthur Holly Compton was an American physicist and Nobel laureate in physics for his discovery of the Compton effect. He served as Chancellor of Washington University in St. Louis from 1945 to 1953.-Early years:...
in his explanation of the scattering of photon
Photon
In physics, a photon is an elementary particle, the quantum of the electromagnetic interaction and the basic unit of light and all other forms of electromagnetic radiation. It is also the force carrier for the electromagnetic force...
s by electron
Electron
The electron is a subatomic particle with a negative elementary electric charge. It has no known components or substructure; in other words, it is generally thought to be an elementary particle. An electron has a mass that is approximately 1/1836 that of the proton...
s (a process known as Compton scattering
Compton scattering
In physics, Compton scattering is a type of scattering that X-rays and gamma rays undergo in matter. The inelastic scattering of photons in matter results in a decrease in energy of an X-ray or gamma ray photon, called the Compton effect...
). The Compton wavelength of a particle is equivalent to the wavelength
Wavelength
In physics, the wavelength of a sinusoidal wave is the spatial period of the wave—the distance over which the wave's shape repeats.It is usually determined by considering the distance between consecutive corresponding points of the same phase, such as crests, troughs, or zero crossings, and is a...
of a photon whose energy is the same as the rest-mass energy of the particle.
The Compton wavelength, λ, of a particle is given by
where h is the Planck constant
Planck constant
The Planck constant , also called Planck's constant, is a physical constant reflecting the sizes of energy quanta in quantum mechanics. It is named after Max Planck, one of the founders of quantum theory, who discovered it in 1899...
, m is the particle's rest mass
Mass
Mass can be defined as a quantitive measure of the resistance an object has to change in its velocity.In physics, mass commonly refers to any of the following three properties of matter, which have been shown experimentally to be equivalent:...
, and c is the speed of light
Speed of light
The speed of light in vacuum, usually denoted by c, is a physical constant important in many areas of physics. Its value is 299,792,458 metres per second, a figure that is exact since the length of the metre is defined from this constant and the international standard for time...
. The significance of this formula is shown in the derivation of the Compton shift formula.
The CODATA 2006 value for the Compton wavelength of the electron is . Other particles have different Compton wavelengths.
Reduced Compton wavelength
When the Compton wavelength is divided by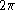, one obtains a smaller or “reduced” Compton wavelength:
The reduced Compton wavelength is a natural representation for mass on the quantum scale, and as such, it appears in many of the fundamental equations of quantum mechanics. The reduced Compton wavelength appears in the relativistic Klein–Gordon equation for a free particle:
It appears in the Dirac equation
Dirac equation
The Dirac equation is a relativistic quantum mechanical wave equation formulated by British physicist Paul Dirac in 1928. It provided a description of elementary spin-½ particles, such as electrons, consistent with both the principles of quantum mechanics and the theory of special relativity, and...
(the following is an explicitly covariant form employing the Einstein summation convention
Einstein notation
In mathematics, especially in applications of linear algebra to physics, the Einstein notation or Einstein summation convention is a notational convention useful when dealing with coordinate formulae...
):
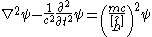
The reduced Compton wavelength also appears in Schrödinger's equation, although its presence is obscured in traditional representations of the equation. The following is the traditional representation of Schrödinger's equation for an electron in a hydrogen-like atom
Hydrogen-like atom
A hydrogen-like ion is any atomic nucleus with one electron and thus is isoelectronic with hydrogen. Except for the hydrogen atom itself , these ions carry the positive charge e, where Z is the atomic number of the atom. Examples of hydrogen-like ions are He+, Li2+, Be3+ and B4+...
:
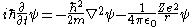
Dividing through by
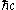, and rewriting in terms of the fine structure constant, one obtains:
Relationship between the reduced and non-reduced Compton wavelength
The reduced Compton wavelength is a natural representation for mass on the quantum scale. Equations that pertain to mass in the form of mass, like Klein-Gordon and Schrödinger's, use the reduced Compton wavelength. The non-reduced Compton wavelength is a natural representation for mass that has been converted into energy. Equations that pertain to the conversion of mass into energy, or to the wavelengths of photons interacting with mass, use the non-reduced Compton wavelength.A particle of rest mass m has a rest energy of .
The non-reduced Compton wavelength for this particle is the wavelength of a photon of the same energy. For photons of frequency
Frequency
Frequency is the number of occurrences of a repeating event per unit time. It is also referred to as temporal frequency.The period is the duration of one cycle in a repeating event, so the period is the reciprocal of the frequency...
f, energy is given by
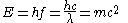
which yields the non-reduced Compton wavelength formula if solved for λ.
Limitation on measurement
The reduced Compton wavelength can be thought of as a fundamental limitation on measuring the position of a particle, taking quantum mechanicsQuantum mechanics
Quantum mechanics, also known as quantum physics or quantum theory, is a branch of physics providing a mathematical description of much of the dual particle-like and wave-like behavior and interactions of energy and matter. It departs from classical mechanics primarily at the atomic and subatomic...
and special relativity
Special relativity
Special relativity is the physical theory of measurement in an inertial frame of reference proposed in 1905 by Albert Einstein in the paper "On the Electrodynamics of Moving Bodies".It generalizes Galileo's...
into account.
This depends on the mass m of the particle.
To see this, note that we can measure the position of a particle
by bouncing light off it - but measuring the position accurately requires light of short wavelength. Light with a short wavelength consists of photons of high energy. If the energy of these photons exceeds mc2, when one hits the particle whose position is being measured the collision may have enough energy to create a new particle of the same type. This
renders moot the question of the original particle's location.
This argument also shows that the reduced Compton wavelength is the cutoff below which quantum field theory
Quantum field theory
Quantum field theory provides a theoretical framework for constructing quantum mechanical models of systems classically parametrized by an infinite number of dynamical degrees of freedom, that is, fields and many-body systems. It is the natural and quantitative language of particle physics and...
– which can describe particle creation and annihilation – becomes important.
We can make the above argument a bit more precise as follows. Suppose we wish to measure the position of a particle to within an accuracy Δx.
Then the uncertainty relation
Uncertainty principle
In quantum mechanics, the Heisenberg uncertainty principle states a fundamental limit on the accuracy with which certain pairs of physical properties of a particle, such as position and momentum, can be simultaneously known...
for position and momentum
Momentum
In classical mechanics, linear momentum or translational momentum is the product of the mass and velocity of an object...
says that
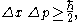
so the uncertainty in the particle's momentum satisfies
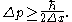
Using the relativistic relation between momentum and energy , when Δp exceeds mc then the uncertainty in energy is greater than mc2, which is enough energy
Mass in special relativity
Mass in special relativity incorporates the general understandings from the concept of mass-energy equivalence. Added to this concept is an additional complication resulting from the fact that "mass" is defined in two different ways in special relativity: one way defines mass as an invariant...
to create another particle of the same type. It follows that there is a fundamental limitation on Δx:
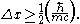
Thus the uncertainty in position must be greater than half of the reduced Compton wavelength ħ/mc.
The Compton wavelength can be contrasted with the de Broglie wavelength, which depends on the momentum of a particle and determines the cutoff between particle and wave behavior in quantum mechanics
Quantum mechanics
Quantum mechanics, also known as quantum physics or quantum theory, is a branch of physics providing a mathematical description of much of the dual particle-like and wave-like behavior and interactions of energy and matter. It departs from classical mechanics primarily at the atomic and subatomic...
.
Relationship to other constants
Typical atomic lengths, wave numbers, and areas in physics can be related to the Compton wavelength and the electromagnetic fine structure constant ()The Bohr radius
Bohr radius
The Bohr radius is a physical constant, approximately equal to the most probable distance between the proton and electron in a hydrogen atom in its ground state. It is named after Niels Bohr, due to its role in the Bohr model of an atom...
is related to the Compton wavelength by:
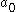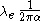
= The classical electron radius
Classical electron radius
The classical electron radius, also known as the Lorentz radius or the Thomson scattering length, is based on a classical relativistic model of the electron...
is written:
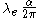
= The Rydberg constant
Rydberg constant
The Rydberg constant, symbol R∞, named after the Swedish physicist Johannes Rydberg, is a physical constant relating to atomic spectra in the science of spectroscopy. Rydberg initially determined its value empirically from spectroscopy, but Niels Bohr later showed that its value could be calculated...
is written:
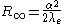
For fermion
Fermion
In particle physics, a fermion is any particle which obeys the Fermi–Dirac statistics . Fermions contrast with bosons which obey Bose–Einstein statistics....
s, the non-reduced Compton wavelength sets the cross-section of interactions. For example, the cross-section for Thomson scattering
Thomson scattering
Thomson scattering is the elastic scattering of electromagnetic radiation by a free charged particle, as described by classical electromagnetism. It is just the low-energy limit of Compton scattering: the particle kinetic energy and photon frequency are the same before and after the scattering...
of a photon from an electron is equal to
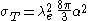,For gauge
Gauge theory
In physics, gauge invariance is the property of a field theory in which different configurations of the underlying fundamental but unobservable fields result in identical observable quantities. A theory with such a property is called a gauge theory...
boson
Boson
In particle physics, bosons are subatomic particles that obey Bose–Einstein statistics. Several bosons can occupy the same quantum state. The word boson derives from the name of Satyendra Nath Bose....
s, the Compton wavelength sets the effective range of the Yukawa interaction
Yukawa interaction
In particle physics, Yukawa's interaction, named after Hideki Yukawa, is an interaction between a scalar field \phi and a Dirac field \Psi of the typeV \approx g\bar\Psi \phi \Psi or g \bar \Psi \gamma^5 \phi \Psi ....
: since the photon
Photon
In physics, a photon is an elementary particle, the quantum of the electromagnetic interaction and the basic unit of light and all other forms of electromagnetic radiation. It is also the force carrier for the electromagnetic force...
has no rest mass, electromagnetism has infinite range.
Typical lengths and areas in gravitational physics can be related to the Compton wavelength and the gravitational coupling constant
Gravitational coupling constant
In physics, the gravitational coupling constant, αG, is the coupling constant characterizing the gravitational attraction between two charged elementary particles having nonzero mass...
(
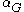which is the gravitational analog of the fine structure constant):The Planck mass is special because the reduced Compton wavelength for this mass is equal to half of the Schwarzschild radius
Schwarzschild radius
The Schwarzschild radius is the distance from the center of an object such that, if all the mass of the object were compressed within that sphere, the escape speed from the surface would equal the speed of light...
. This special distance is called the Planck length (
). This is a simple case of dimensional analysisDimensional analysis
In physics and all science, dimensional analysis is a tool to find or check relations among physical quantities by using their dimensions. The dimension of a physical quantity is the combination of the basic physical dimensions which describe it; for example, speed has the dimension length per...
: the Schwarzschild radius is proportional to the mass, whereas the Compton wavelength is proportional to the inverse of the mass. The Planck length is written: