Yukawa interaction
Encyclopedia
In particle physics
, Yukawa's interaction, named after Hideki Yukawa
, is an interaction between a scalar field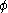
and a Dirac field 
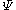of the type
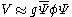(scalar) or 
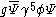(pseudoscalar
).
The Yukawa interaction can be used to describe the strong nuclear force between nucleon
s (which are fermion
s), mediated by pion
s (which are pseudoscalar meson
s). The Yukawa interaction is also used in the Standard Model
to describe the coupling between the Higgs field and massless quark
and lepton
fields (i.e., the fundamental fermion particles). Through spontaneous symmetry breaking
, these fermions acquire a mass proportional to the vacuum expectation value
of the Higgs field.
for a meson
field φ interacting with a Dirac baryon
field ψ is
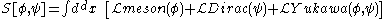
where the integration is performed over d dimensions (typically 4 for four-dimensional spacetime). The meson Lagrangian
is given by
.
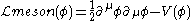Here,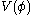
is a self-interaction term. For a free-field massive meson, one would have 
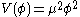where 
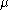is the mass for the meson. For a (renormalizable) self-interacting field, one will have 
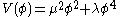where λ is a coupling constant. This potential is explored in detail in the article on the quartic interaction.
The free-field Dirac Lagrangian is given by
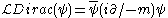
where m is the positive, real mass of the fermion.
The Yukawa interaction term is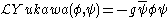
where g is the (real) coupling constant
for scalar mesons and
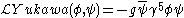
for pseudoscalar mesons. Putting it all together one can write the above more explicitly as
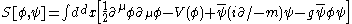
which is the same as a Coulomb potential except for the sign and the exponential factor. The sign will make the interaction attractive between all particles (the electromagnetic interaction is repulsive for identical particles). This is explained by the fact that the Yukawa particle has spin zero and even spin always results in an attractive potential. The exponential will give the interaction a finite range, so that particles at great distances will hardly interact any longer.
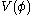has a minimum not at 
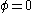but at some non-zero value 
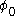. This can happen if one writes (for example) 
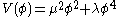and then sets μ to an imaginary value. In this case, one says that the Lagrangian exhibits spontaneous symmetry breaking
. The non-zero value of φ is called the vacuum expectation value
of φ. In the Standard Model
, this non-zero value is responsible for the fermion masses, as shown below.
To exhibit the mass term, one re-expresses the action in terms of the field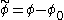
, where 
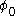is now understood to be a constant independent of position. We now see that the Yukawa term has a component
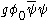
and since both g and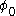
are constants, this term looks exactly like a mass term for a fermion with mass 
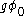. This is the mechanism by which spontaneous symmetry breaking gives mass to fermions. The field 
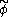is known as the Higgs field.
Majorana spinors, one has
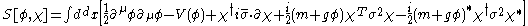
where g is a complex coupling constant
and m is a complex number
.
from a Feynman diagram
involving the Yukawa interaction.
Particle physics
Particle physics is a branch of physics that studies the existence and interactions of particles that are the constituents of what is usually referred to as matter or radiation. In current understanding, particles are excitations of quantum fields and interact following their dynamics...
, Yukawa's interaction, named after Hideki Yukawa
Hideki Yukawa
né , was a Japanese theoretical physicist and the first Japanese Nobel laureate.-Biography:Yukawa was born in Tokyo and grew up in Kyoto. In 1929, after receiving his degree from Kyoto Imperial University, he stayed on as a lecturer for four years. After graduation, he was interested in...
, is an interaction between a scalar field
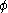and a Dirac field 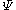of the type 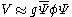(scalar) or 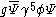(pseudoscalarPseudoscalar
In physics, a pseudoscalar is a quantity that behaves like a scalar, except that it changes sign under a parity inversion such as improper rotations while a true scalar does not.The prototypical example of a pseudoscalar is the scalar triple product...
).
The Yukawa interaction can be used to describe the strong nuclear force between nucleon
Nucleon
In physics, a nucleon is a collective name for two particles: the neutron and the proton. These are the two constituents of the atomic nucleus. Until the 1960s, the nucleons were thought to be elementary particles...
s (which are fermion
Fermion
In particle physics, a fermion is any particle which obeys the Fermi–Dirac statistics . Fermions contrast with bosons which obey Bose–Einstein statistics....
s), mediated by pion
Pion
In particle physics, a pion is any of three subatomic particles: , , and . Pions are the lightest mesons and they play an important role in explaining the low-energy properties of the strong nuclear force....
s (which are pseudoscalar meson
Meson
In particle physics, mesons are subatomic particles composed of one quark and one antiquark, bound together by the strong interaction. Because mesons are composed of sub-particles, they have a physical size, with a radius roughly one femtometer: 10−15 m, which is about the size of a proton...
s). The Yukawa interaction is also used in the Standard Model
Standard Model
The Standard Model of particle physics is a theory concerning the electromagnetic, weak, and strong nuclear interactions, which mediate the dynamics of the known subatomic particles. Developed throughout the mid to late 20th century, the current formulation was finalized in the mid 1970s upon...
to describe the coupling between the Higgs field and massless quark
Quark
A quark is an elementary particle and a fundamental constituent of matter. Quarks combine to form composite particles called hadrons, the most stable of which are protons and neutrons, the components of atomic nuclei. Due to a phenomenon known as color confinement, quarks are never directly...
and lepton
Lepton
A lepton is an elementary particle and a fundamental constituent of matter. The best known of all leptons is the electron which governs nearly all of chemistry as it is found in atoms and is directly tied to all chemical properties. Two main classes of leptons exist: charged leptons , and neutral...
fields (i.e., the fundamental fermion particles). Through spontaneous symmetry breaking
Spontaneous symmetry breaking
Spontaneous symmetry breaking is the process by which a system described in a theoretically symmetrical way ends up in an apparently asymmetric state....
, these fermions acquire a mass proportional to the vacuum expectation value
Vacuum expectation value
In quantum field theory the vacuum expectation value of an operator is its average, expected value in the vacuum. The vacuum expectation value of an operator O is usually denoted by \langle O\rangle...
of the Higgs field.
The action
The actionAction (physics)
In physics, action is an attribute of the dynamics of a physical system. It is a mathematical functional which takes the trajectory, also called path or history, of the system as its argument and has a real number as its result. Action has the dimension of energy × time, and its unit is...
for a meson
Meson
In particle physics, mesons are subatomic particles composed of one quark and one antiquark, bound together by the strong interaction. Because mesons are composed of sub-particles, they have a physical size, with a radius roughly one femtometer: 10−15 m, which is about the size of a proton...
field φ interacting with a Dirac baryon
Baryon
A baryon is a composite particle made up of three quarks . Baryons and mesons belong to the hadron family, which are the quark-based particles...
field ψ is
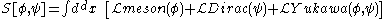
where the integration is performed over d dimensions (typically 4 for four-dimensional spacetime). The meson Lagrangian
Lagrangian
The Lagrangian, L, of a dynamical system is a function that summarizes the dynamics of the system. It is named after Joseph Louis Lagrange. The concept of a Lagrangian was originally introduced in a reformulation of classical mechanics by Irish mathematician William Rowan Hamilton known as...
is given by
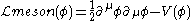.Here,
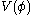is a self-interaction term. For a free-field massive meson, one would hav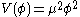e where 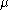is the mass for the meson. For a (renormalizable) self-interacting field, one will have 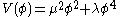where λ is a coupling constant. This potential is explored in detail in the article on the quartic interaction.The free-field Dirac Lagrangian is given by
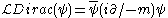
where m is the positive, real mass of the fermion.
The Yukawa interaction term is
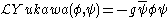
where g is the (real) coupling constant
Coupling constant
In physics, a coupling constant, usually denoted g, is a number that determines the strength of an interaction. Usually the Lagrangian or the Hamiltonian of a system can be separated into a kinetic part and an interaction part...
for scalar mesons and
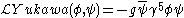
for pseudoscalar mesons. Putting it all together one can write the above more explicitly as
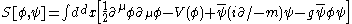
Classical potential
If two fermions interact through a Yukawa interaction with Yukawa particle mass μ, the potential between the two particles, known as the Yukawa potential, will be:- V(r) =
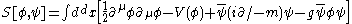
which is the same as a Coulomb potential except for the sign and the exponential factor. The sign will make the interaction attractive between all particles (the electromagnetic interaction is repulsive for identical particles). This is explained by the fact that the Yukawa particle has spin zero and even spin always results in an attractive potential. The exponential will give the interaction a finite range, so that particles at great distances will hardly interact any longer.
Spontaneous symmetry breaking
Now suppose that the potential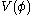 has a minimum not at 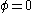but at some non-zero value 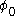. This can happen if one writes (for example) 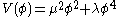and then sets μ to an imaginary value. In this case, one says that the Lagrangian exhibits spontaneous symmetry breakingSpontaneous symmetry breaking
Spontaneous symmetry breaking is the process by which a system described in a theoretically symmetrical way ends up in an apparently asymmetric state....
. The non-zero value of φ is called the vacuum expectation value
Vacuum expectation value
In quantum field theory the vacuum expectation value of an operator is its average, expected value in the vacuum. The vacuum expectation value of an operator O is usually denoted by \langle O\rangle...
of φ. In the Standard Model
Standard Model
The Standard Model of particle physics is a theory concerning the electromagnetic, weak, and strong nuclear interactions, which mediate the dynamics of the known subatomic particles. Developed throughout the mid to late 20th century, the current formulation was finalized in the mid 1970s upon...
, this non-zero value is responsible for the fermion masses, as shown below.
To exhibit the mass term, one re-expresses the action in terms of the field
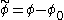, where 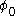is now understood to be a constant independent of position. We now see that the Yukawa term has a component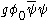and since both g and
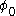are constants, this term looks exactly like a mass term for a fermion with mass 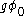. This is the mechanism by which spontaneous symmetry breaking gives mass to fermions. The field 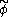is known as the Higgs field.Majorana form
It's also possible to have a Yukawa interaction between a scalar and a Majorana field. In fact, the Yukawa interaction involving a scalar and a Dirac spinor can be thought of as a Yukawa interaction involving a scalar with two Majorana spinors of the same mass. Broken out in terms of the two chiralChirality (physics)
A chiral phenomenon is one that is not identical to its mirror image . The spin of a particle may be used to define a handedness for that particle. A symmetry transformation between the two is called parity...
Majorana spinors, one has
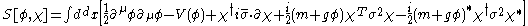
where g is a complex coupling constant
Coupling constant
In physics, a coupling constant, usually denoted g, is a number that determines the strength of an interaction. Usually the Lagrangian or the Hamiltonian of a system can be separated into a kinetic part and an interaction part...
and m is a complex number
Complex number
A complex number is a number consisting of a real part and an imaginary part. Complex numbers extend the idea of the one-dimensional number line to the two-dimensional complex plane by using the number line for the real part and adding a vertical axis to plot the imaginary part...
.
Feynman rules
The article Yukawa potential provides a simple example of the Feynman rules and a calculation of a scattering amplitudeScattering amplitude
In quantum physics, the scattering amplitude is the amplitude of the outgoing spherical wave relative to the incoming plane wave in the stationary-state scattering process...
from a Feynman diagram
Feynman diagram
Feynman diagrams are a pictorial representation scheme for the mathematical expressions governing the behavior of subatomic particles, first developed by the Nobel Prize-winning American physicist Richard Feynman, and first introduced in 1948...
involving the Yukawa interaction.