Quartic interaction
Encyclopedia
This article refers to a type of self-interaction in scalar field theory
, a topic in quantum field theory
. Other types of quartic interactions may be found under the topic of four-fermion interactions. A classical free scalar field φ satisfies the Klein-Gordon equation
. If a scalar field is denoted φ, a quartic interaction is represented by adding a potential term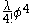
. The coupling constant
λ is dimensionless in 4-dimensional space-time.
This article uses the (+−−−) metric signature
for Minkowski space
.
for a real
scalar field takes the form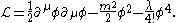
This Lagrangian has a global Z2 symmetry mapping φ to −φ. For a complex
scalar field the Lagrangian is,
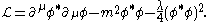
With n real scalar fields, we can have a φ4 model with a global
SO(N) symmetry
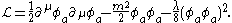
Expanding the complex field in real and imaginary parts shows that it is equivalent to the SO(2) model of real scalar fields.
In all of the models above, the coupling constant
λ must have a non-negative real part, since otherwise, the potential is unbounded below, and there can be no stable vacuum. Also, the Feynman path integral discussed below would be ill-defined. In 4 dimensions, φ4 theories have a Landau pole
. This means that without a cut-off on the high-energy scale, renormalization
would render the theory trivial
.
expansion may be obtained also from the Feynman path integral formulation
. The time ordered vacuum expectation value
s of polynomials in φ, known as the n-particle Green's functions, are constructed by integrating over all possible fields, normalized by the vacuum expectation value
with no external fields,
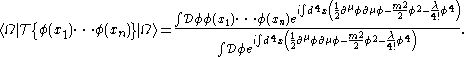
All of these Green's functions may be obtained by expanding the exponential in J(x)φ(x) in the generating function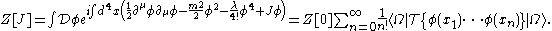
A Wick rotation
may be applied to make time imaginary. Changing the signature to (++++) then gives a φ4 statistical mechanics
integral over a 4-dimensional Euclidean space
,
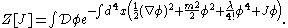
Normally, this is applied to the scattering of particles with fixed momenta, in which case, a Fourier transform
is useful, giving instead
The standard trick to evaluate this functional integral is to write it as a product of exponential factors, schematically,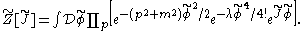
The second two exponential factors can be expanded as power series, and the combinatorics of this expansion can be represented graphically. The integral with λ = 0 can be treated as a product of infinitely many elementary Gaussian integrals, and the result may be expressed as a sum of Feynman diagrams, calculated using the following Feynman rules:
The last rule takes into account the effect of dividing by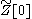
. The Minkowski-space Feynman rules are similar, except that each vertex is represented by 
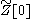, while each internal line is represented by a factor i/(q2-m2 + i ε), where the ε term represents the small Wick rotation needed to make the Minkowski-space Gaussian integral converge.
, which is a procedure of adding divergent counter-terms to the Lagrangian in such a way that the diagrams constructed from the original Lagrangian and counter-terms is finite. A renormalization scale must be introduced in the process, and the coupling constant and mass become dependent upon it. It is this dependence that leads to the Landau pole
mentioned earlier, and requires that the cutoff be kept finite. Alternatively, if the cutoff is allowed to go to infinity, the Landau pole can be avoided only by if the renormalized coupling runs to zero, rendering the theory trivial
.
s. In the O(2) theory, the vacua would lie on a circle, and the choice of one would spontaneously break the O(2) theory. A continuous broken symmetry leads to a Goldstone boson
. This type of spontaneous symmetry breaking is the essential component of the Higgs mechanism
.
Scalar field theory
In theoretical physics, scalar field theory can refer to a classical or quantum theory of scalar fields. A field which is invariant under any Lorentz transformation is called a "scalar", in contrast to a vector or tensor field...
, a topic in quantum field theory
Quantum field theory
Quantum field theory provides a theoretical framework for constructing quantum mechanical models of systems classically parametrized by an infinite number of dynamical degrees of freedom, that is, fields and many-body systems. It is the natural and quantitative language of particle physics and...
. Other types of quartic interactions may be found under the topic of four-fermion interactions. A classical free scalar field φ satisfies the Klein-Gordon equation
Klein-Gordon equation
The Klein–Gordon equation is a relativistic version of the Schrödinger equation....
. If a scalar field is denoted φ, a quartic interaction is represented by adding a potential term
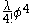. The coupling constantCoupling constant
In physics, a coupling constant, usually denoted g, is a number that determines the strength of an interaction. Usually the Lagrangian or the Hamiltonian of a system can be separated into a kinetic part and an interaction part...
λ is dimensionless in 4-dimensional space-time.
This article uses the (+−−−) metric signature
Metric signature
The signature of a metric tensor is the number of positive and negative eigenvalues of the metric. That is, the corresponding real symmetric matrix is diagonalised, and the diagonal entries of each sign counted...
for Minkowski space
Minkowski space
In physics and mathematics, Minkowski space or Minkowski spacetime is the mathematical setting in which Einstein's theory of special relativity is most conveniently formulated...
.
The Lagrangian
The LagrangianLagrangian
The Lagrangian, L, of a dynamical system is a function that summarizes the dynamics of the system. It is named after Joseph Louis Lagrange. The concept of a Lagrangian was originally introduced in a reformulation of classical mechanics by Irish mathematician William Rowan Hamilton known as...
for a real
Real number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
scalar field takes the form
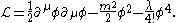
This Lagrangian has a global Z2 symmetry mapping φ to −φ. For a complex
Complex number
A complex number is a number consisting of a real part and an imaginary part. Complex numbers extend the idea of the one-dimensional number line to the two-dimensional complex plane by using the number line for the real part and adding a vertical axis to plot the imaginary part...
scalar field the Lagrangian is,
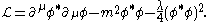
With n real scalar fields, we can have a φ4 model with a global
Global symmetry
A global symmetry is a symmetry that holds at all points in the spacetime under consideration, as opposed to a local symmetry which varies from point to point.Global symmetries require conservation laws, but not forces, in physics.-See also:...
SO(N) symmetry
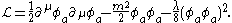
Expanding the complex field in real and imaginary parts shows that it is equivalent to the SO(2) model of real scalar fields.
In all of the models above, the coupling constant
Coupling constant
In physics, a coupling constant, usually denoted g, is a number that determines the strength of an interaction. Usually the Lagrangian or the Hamiltonian of a system can be separated into a kinetic part and an interaction part...
λ must have a non-negative real part, since otherwise, the potential is unbounded below, and there can be no stable vacuum. Also, the Feynman path integral discussed below would be ill-defined. In 4 dimensions, φ4 theories have a Landau pole
Landau pole
In physics, the Landau pole is the momentum scale at which the coupling constant of a quantum field theory becomes infinite...
. This means that without a cut-off on the high-energy scale, renormalization
Renormalization
In quantum field theory, the statistical mechanics of fields, and the theory of self-similar geometric structures, renormalization is any of a collection of techniques used to treat infinities arising in calculated quantities....
would render the theory trivial
Quantum triviality
In a quantum field theory, charge screening can restrict the value of the observable "renormalized" charge of a classical theory. Ifthe only allowed value of the renormalized charge is zero, the theory is said to be "trivial" or noninteracting...
.
Feynman Integral Quantization
The Feynman diagramFeynman diagram
Feynman diagrams are a pictorial representation scheme for the mathematical expressions governing the behavior of subatomic particles, first developed by the Nobel Prize-winning American physicist Richard Feynman, and first introduced in 1948...
expansion may be obtained also from the Feynman path integral formulation
Path integral formulation
The path integral formulation of quantum mechanics is a description of quantum theory which generalizes the action principle of classical mechanics...
. The time ordered vacuum expectation value
Vacuum expectation value
In quantum field theory the vacuum expectation value of an operator is its average, expected value in the vacuum. The vacuum expectation value of an operator O is usually denoted by \langle O\rangle...
s of polynomials in φ, known as the n-particle Green's functions, are constructed by integrating over all possible fields, normalized by the vacuum expectation value
Vacuum expectation value
In quantum field theory the vacuum expectation value of an operator is its average, expected value in the vacuum. The vacuum expectation value of an operator O is usually denoted by \langle O\rangle...
with no external fields,
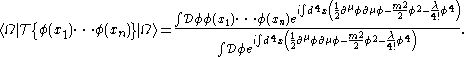
All of these Green's functions may be obtained by expanding the exponential in J(x)φ(x) in the generating function
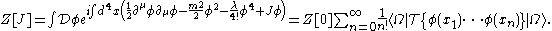
A Wick rotation
Wick rotation
In physics, Wick rotation, named after Gian-Carlo Wick, is a method of finding a solution to a mathematical problem in Minkowski space from a solution to a related problem in Euclidean space by means of a transformation that substitutes an imaginary-number variable for a real-number variable...
may be applied to make time imaginary. Changing the signature to (++++) then gives a φ4 statistical mechanics
Statistical mechanics
Statistical mechanics or statistical thermodynamicsThe terms statistical mechanics and statistical thermodynamics are used interchangeably...
integral over a 4-dimensional Euclidean space
Euclidean space
In mathematics, Euclidean space is the Euclidean plane and three-dimensional space of Euclidean geometry, as well as the generalizations of these notions to higher dimensions...
,
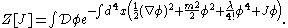
Normally, this is applied to the scattering of particles with fixed momenta, in which case, a Fourier transform
Fourier transform
In mathematics, Fourier analysis is a subject area which grew from the study of Fourier series. The subject began with the study of the way general functions may be represented by sums of simpler trigonometric functions...
is useful, giving instead
The standard trick to evaluate this functional integral is to write it as a product of exponential factors, schematically,
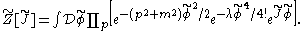
The second two exponential factors can be expanded as power series, and the combinatorics of this expansion can be represented graphically. The integral with λ = 0 can be treated as a product of infinitely many elementary Gaussian integrals, and the result may be expressed as a sum of Feynman diagrams, calculated using the following Feynman rules:
- Each field
in the n-point Euclidean Green's function is represented by an external line (half-edge) in the graph, and associated with momentum p. - Each vertex is represented by a factor -λ.
- At a given order λk, all diagrams with n external lines and k vertices are constructed such that the momenta flowing into each vertex is zero. Each internal line is represented by a factor 1/(q2 + m2), where q is the momentum flowing through that line.
- Any unconstrained momenta are integrated over all values.
- The result is divided by a symmetry factor, which is the number of ways the lines and vertices of the graph can be rearranged without changing its connectivity.
- Do not include graphs containing "vacuum bubbles", connected subgraphs with no external lines.
The last rule takes into account the effect of dividing by
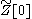. The Minkowski-space Feynman rules are similar, except that each vertex is represented by 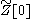, while each internal line is represented by a factor i/(q2-m2 + i ε), where the ε term represents the small Wick rotation needed to make the Minkowski-space Gaussian integral converge.Renormalization
The integrals over unconstrained momenta, called "loop integrals", in the Feynman graphs typically diverge. This is normally handled by renormalizationRenormalization
In quantum field theory, the statistical mechanics of fields, and the theory of self-similar geometric structures, renormalization is any of a collection of techniques used to treat infinities arising in calculated quantities....
, which is a procedure of adding divergent counter-terms to the Lagrangian in such a way that the diagrams constructed from the original Lagrangian and counter-terms is finite. A renormalization scale must be introduced in the process, and the coupling constant and mass become dependent upon it. It is this dependence that leads to the Landau pole
Landau pole
In physics, the Landau pole is the momentum scale at which the coupling constant of a quantum field theory becomes infinite...
mentioned earlier, and requires that the cutoff be kept finite. Alternatively, if the cutoff is allowed to go to infinity, the Landau pole can be avoided only by if the renormalized coupling runs to zero, rendering the theory trivial
Quantum triviality
In a quantum field theory, charge screening can restrict the value of the observable "renormalized" charge of a classical theory. Ifthe only allowed value of the renormalized charge is zero, the theory is said to be "trivial" or noninteracting...
.
Spontaneous symmetry breaking
An interesting feature can occur if m2 happens to be negative, but with λ positive. In this case, the vacuum consists of two lowest-energy states, each of which spontaneously breaks the Z2 global symmetry of the original theory. This leads to the appearance of interesting collective states like domain wallDomain wall
A domain wall is a term used in physics which can have one of two distinct but similar meanings in magnetism, optics, or string theory. These phenomena can all be generically described as topological solitons which occur whenever a discrete symmetry is spontaneously broken.-Magnetism:In magnetism,...
s. In the O(2) theory, the vacua would lie on a circle, and the choice of one would spontaneously break the O(2) theory. A continuous broken symmetry leads to a Goldstone boson
Goldstone boson
In particle and condensed matter physics, Goldstone bosons or Nambu–Goldstone bosons are bosons that appear necessarily in models exhibiting spontaneous breakdown of continuous symmetries...
. This type of spontaneous symmetry breaking is the essential component of the Higgs mechanism
Higgs mechanism
In particle physics, the Higgs mechanism is the process in which gauge bosons in a gauge theory can acquire non-vanishing masses through absorption of Nambu-Goldstone bosons arising in spontaneous symmetry breaking....
.
See also
- Scalar field theoryScalar field theoryIn theoretical physics, scalar field theory can refer to a classical or quantum theory of scalar fields. A field which is invariant under any Lorentz transformation is called a "scalar", in contrast to a vector or tensor field...
- Quantum trivialityQuantum trivialityIn a quantum field theory, charge screening can restrict the value of the observable "renormalized" charge of a classical theory. Ifthe only allowed value of the renormalized charge is zero, the theory is said to be "trivial" or noninteracting...
- Landau poleLandau poleIn physics, the Landau pole is the momentum scale at which the coupling constant of a quantum field theory becomes infinite...
- RenormalizationRenormalizationIn quantum field theory, the statistical mechanics of fields, and the theory of self-similar geometric structures, renormalization is any of a collection of techniques used to treat infinities arising in calculated quantities....
- Higgs mechanismHiggs mechanismIn particle physics, the Higgs mechanism is the process in which gauge bosons in a gauge theory can acquire non-vanishing masses through absorption of Nambu-Goldstone bosons arising in spontaneous symmetry breaking....
- Goldstone bosonGoldstone bosonIn particle and condensed matter physics, Goldstone bosons or Nambu–Goldstone bosons are bosons that appear necessarily in models exhibiting spontaneous breakdown of continuous symmetries...