
Wick rotation
Encyclopedia
In physics
, Wick rotation, named after Gian-Carlo Wick
, is a method of finding a solution to a mathematical problem in Minkowski space
from a solution to a related problem in Euclidean space
by means of a transformation that substitutes an imaginary-number variable for a real-number variable. This transformation is also used to find solutions to problems in quantum mechanics and other areas.
(with (−1, +1, +1, +1) convention for the metric tensor)
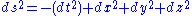
and the four-dimensional Euclidean metric

are equivalent if one permits the coordinate t to take on imaginary
values. The Minkowski metric becomes Euclidean when t is restricted to the imaginary axis
, and vice versa. Taking a problem expressed in Minkowski space with coordinates x, y, z, t, and substituting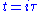 , sometimes yields a problem in real Euclidean coordinates x, y, z,
, sometimes yields a problem in real Euclidean coordinates x, y, z,  which is easier to solve. This solution may then, under reverse substitution, yield a solution to the original problem.
which is easier to solve. This solution may then, under reverse substitution, yield a solution to the original problem.
to quantum mechanics
by replacing inverse temperature with imaginary time
with imaginary time 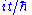 . Consider a large collection of harmonic oscillator
. Consider a large collection of harmonic oscillator
s at temperature
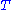 . The relative probability of finding any given oscillator with energy
. The relative probability of finding any given oscillator with energy 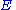 is
is  , where
, where 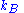 is Boltzmann's constant. The average value of an observable
is Boltzmann's constant. The average value of an observable  is, up to a normalizing constant,
is, up to a normalizing constant,
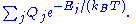
Now consider a single quantum harmonic oscillator
in a superposition
of basis states, evolving for a time under a Hamiltonian
under a Hamiltonian  . The relative phase change of the basis state with energy
. The relative phase change of the basis state with energy 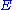 is
is 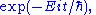 where
where  is Planck's constant. The probability amplitude
is Planck's constant. The probability amplitude
that a uniform superposition of states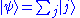 evolves to an arbitrary superposition
evolves to an arbitrary superposition  is, up to a normalizing constant,
is, up to a normalizing constant,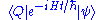
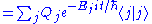
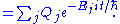
 dimensions to dynamics problems in
dimensions to dynamics problems in  dimensions, trading one dimension of space for one dimension of time. A simple example where
dimensions, trading one dimension of space for one dimension of time. A simple example where  is a hanging spring with fixed endpoints in a gravitational field. The shape of the spring is a curve
is a hanging spring with fixed endpoints in a gravitational field. The shape of the spring is a curve 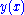 . The spring is in equilibrium when the energy associated with this curve is at a critical point; this critical point is typically a minimum, so this idea is usually called "the principle of least energy". To compute the energy, we integrate over the energy density at each point:
. The spring is in equilibrium when the energy associated with this curve is at a critical point; this critical point is typically a minimum, so this idea is usually called "the principle of least energy". To compute the energy, we integrate over the energy density at each point: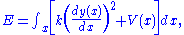
where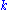 is the spring constant and
is the spring constant and  is the gravitational potential.
is the gravitational potential.
The corresponding dynamics problem is that of a rock thrown upwards; the path the rock follows is a critical point of the action
. Action is the integral of the Lagrangian
; as before, this critical point is typically a minimum, so this is called the "principle of least action
":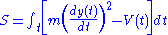
We get the solution to the dynamics problem (up to a factor of ) from the statics problem by Wick rotation, replacing
) from the statics problem by Wick rotation, replacing  by
by  ,
, 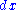 by
by 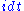 , and the spring constant
, and the spring constant 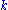 by the mass of the rock
by the mass of the rock  :
:
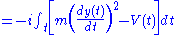
of quantum mechanics is related to statistical mechanics. From statistical mechanics, the shape of each spring in a collection at temperature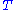 will deviate from the least-energy shape due to thermal fluctuations; the probability of finding a spring with a given shape decreases exponentially with the energy difference from the least-energy shape. Similarly, a quantum particle moving in a potential can be described by a superposition of paths, each with a phase
will deviate from the least-energy shape due to thermal fluctuations; the probability of finding a spring with a given shape decreases exponentially with the energy difference from the least-energy shape. Similarly, a quantum particle moving in a potential can be described by a superposition of paths, each with a phase  : the thermal variations in the shape across the collection have turned into quantum uncertainty in the path of the quantum particle.
: the thermal variations in the shape across the collection have turned into quantum uncertainty in the path of the quantum particle.
and the heat equation
are also related by Wick rotation. However, there is a slight difference. Statistical mechanics n-point functions satisfy positivity whereas Wick-rotated quantum field theories satisfy reflection positivity
.
It is called a rotation because when we represent complex numbers as a plane
, the multiplication of a complex number by i is equivalent to rotating the vector representing that number by an angle
of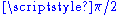 about the origin
about the origin
.
When Stephen Hawking
wrote about "imaginary time" in his famous book A Brief History of Time
, he was referring to Wick rotation.
Wick rotation also relates a QFT at a finite inverse temperature β to a statistical mechanical model over the "tube" R3×S1 with the imaginary time coordinate τ being periodic with period β.
Note, however, that the Wick rotation cannot be viewed as a rotation on a complex vector space that is equipped with the conventional norm and metric induced by the inner product, as in this case the rotation would cancel out and have no effect at all.
Physics
Physics is a natural science that involves the study of matter and its motion through spacetime, along with related concepts such as energy and force. More broadly, it is the general analysis of nature, conducted in order to understand how the universe behaves.Physics is one of the oldest academic...
, Wick rotation, named after Gian-Carlo Wick
Gian-Carlo Wick
Gian Carlo Wick was an Italian theoretical physicist who made important contributions to quantum field theory...
, is a method of finding a solution to a mathematical problem in Minkowski space
Minkowski space
In physics and mathematics, Minkowski space or Minkowski spacetime is the mathematical setting in which Einstein's theory of special relativity is most conveniently formulated...
from a solution to a related problem in Euclidean space
Euclidean space
In mathematics, Euclidean space is the Euclidean plane and three-dimensional space of Euclidean geometry, as well as the generalizations of these notions to higher dimensions...
by means of a transformation that substitutes an imaginary-number variable for a real-number variable. This transformation is also used to find solutions to problems in quantum mechanics and other areas.
Overview
It is motivated by the observation that the Minkowski metricMetric tensor
In the mathematical field of differential geometry, a metric tensor is a type of function defined on a manifold which takes as input a pair of tangent vectors v and w and produces a real number g in a way that generalizes many of the familiar properties of the dot product of vectors in Euclidean...
(with (−1, +1, +1, +1) convention for the metric tensor)
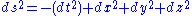
and the four-dimensional Euclidean metric

are equivalent if one permits the coordinate t to take on imaginary
Imaginary number
An imaginary number is any number whose square is a real number less than zero. When any real number is squared, the result is never negative, but the square of an imaginary number is always negative...
values. The Minkowski metric becomes Euclidean when t is restricted to the imaginary axis
Imaginary number
An imaginary number is any number whose square is a real number less than zero. When any real number is squared, the result is never negative, but the square of an imaginary number is always negative...
, and vice versa. Taking a problem expressed in Minkowski space with coordinates x, y, z, t, and substituting
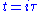 , sometimes yields a problem in real Euclidean coordinates x, y, z,
, sometimes yields a problem in real Euclidean coordinates x, y, z,  which is easier to solve. This solution may then, under reverse substitution, yield a solution to the original problem.
which is easier to solve. This solution may then, under reverse substitution, yield a solution to the original problem.Statistical and quantum mechanics
Wick rotation connects statistical mechanicsStatistical mechanics
Statistical mechanics or statistical thermodynamicsThe terms statistical mechanics and statistical thermodynamics are used interchangeably...
to quantum mechanics
Quantum mechanics
Quantum mechanics, also known as quantum physics or quantum theory, is a branch of physics providing a mathematical description of much of the dual particle-like and wave-like behavior and interactions of energy and matter. It departs from classical mechanics primarily at the atomic and subatomic...
by replacing inverse temperature
 with imaginary time
with imaginary time 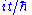 . Consider a large collection of harmonic oscillator
. Consider a large collection of harmonic oscillatorHarmonic oscillator
In classical mechanics, a harmonic oscillator is a system that, when displaced from its equilibrium position, experiences a restoring force, F, proportional to the displacement, x: \vec F = -k \vec x \, where k is a positive constant....
s at temperature
Temperature
Temperature is a physical property of matter that quantitatively expresses the common notions of hot and cold. Objects of low temperature are cold, while various degrees of higher temperatures are referred to as warm or hot...
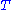 . The relative probability of finding any given oscillator with energy
. The relative probability of finding any given oscillator with energy 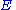 is
is  , where
, where 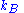 is Boltzmann's constant. The average value of an observable
is Boltzmann's constant. The average value of an observable  is, up to a normalizing constant,
is, up to a normalizing constant,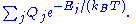
Now consider a single quantum harmonic oscillator
Quantum harmonic oscillator
The quantum harmonic oscillator is the quantum-mechanical analog of the classical harmonic oscillator. Because an arbitrary potential can be approximated as a harmonic potential at the vicinity of a stable equilibrium point, it is one of the most important model systems in quantum mechanics...
in a superposition
Quantum superposition
Quantum superposition is a fundamental principle of quantum mechanics. It holds that a physical system exists in all its particular, theoretically possible states simultaneously; but, when measured, it gives a result corresponding to only one of the possible configurations.Mathematically, it...
of basis states, evolving for a time
 under a Hamiltonian
under a Hamiltonian  . The relative phase change of the basis state with energy
. The relative phase change of the basis state with energy 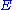 is
is 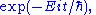 where
where  is Planck's constant. The probability amplitude
is Planck's constant. The probability amplitudeProbability amplitude
In quantum mechanics, a probability amplitude is a complex number whose modulus squared represents a probability or probability density.For example, if the probability amplitude of a quantum state is \alpha, the probability of measuring that state is |\alpha|^2...
that a uniform superposition of states
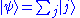 evolves to an arbitrary superposition
evolves to an arbitrary superposition  is, up to a normalizing constant,
is, up to a normalizing constant,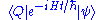
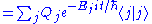
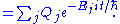
Statics and dynamics
Wick rotation relates statics problems in dimensions to dynamics problems in
dimensions to dynamics problems in  dimensions, trading one dimension of space for one dimension of time. A simple example where
dimensions, trading one dimension of space for one dimension of time. A simple example where  is a hanging spring with fixed endpoints in a gravitational field. The shape of the spring is a curve
is a hanging spring with fixed endpoints in a gravitational field. The shape of the spring is a curve 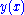 . The spring is in equilibrium when the energy associated with this curve is at a critical point; this critical point is typically a minimum, so this idea is usually called "the principle of least energy". To compute the energy, we integrate over the energy density at each point:
. The spring is in equilibrium when the energy associated with this curve is at a critical point; this critical point is typically a minimum, so this idea is usually called "the principle of least energy". To compute the energy, we integrate over the energy density at each point: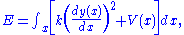
where
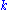 is the spring constant and
is the spring constant and  is the gravitational potential.
is the gravitational potential.The corresponding dynamics problem is that of a rock thrown upwards; the path the rock follows is a critical point of the action
Action (physics)
In physics, action is an attribute of the dynamics of a physical system. It is a mathematical functional which takes the trajectory, also called path or history, of the system as its argument and has a real number as its result. Action has the dimension of energy × time, and its unit is...
. Action is the integral of the Lagrangian
Lagrangian
The Lagrangian, L, of a dynamical system is a function that summarizes the dynamics of the system. It is named after Joseph Louis Lagrange. The concept of a Lagrangian was originally introduced in a reformulation of classical mechanics by Irish mathematician William Rowan Hamilton known as...
; as before, this critical point is typically a minimum, so this is called the "principle of least action
Principle of least action
In physics, the principle of least action – or, more accurately, the principle of stationary action – is a variational principle that, when applied to the action of a mechanical system, can be used to obtain the equations of motion for that system...
":
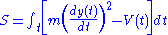
We get the solution to the dynamics problem (up to a factor of
 ) from the statics problem by Wick rotation, replacing
) from the statics problem by Wick rotation, replacing  by
by  ,
, 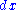 by
by 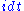 , and the spring constant
, and the spring constant 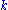 by the mass of the rock
by the mass of the rock  :
:
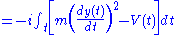
Both thermal/quantum and static/dynamic
Taken together, the previous two examples show how the path integral formulationPath integral formulation
The path integral formulation of quantum mechanics is a description of quantum theory which generalizes the action principle of classical mechanics...
of quantum mechanics is related to statistical mechanics. From statistical mechanics, the shape of each spring in a collection at temperature
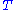 will deviate from the least-energy shape due to thermal fluctuations; the probability of finding a spring with a given shape decreases exponentially with the energy difference from the least-energy shape. Similarly, a quantum particle moving in a potential can be described by a superposition of paths, each with a phase
will deviate from the least-energy shape due to thermal fluctuations; the probability of finding a spring with a given shape decreases exponentially with the energy difference from the least-energy shape. Similarly, a quantum particle moving in a potential can be described by a superposition of paths, each with a phase  : the thermal variations in the shape across the collection have turned into quantum uncertainty in the path of the quantum particle.
: the thermal variations in the shape across the collection have turned into quantum uncertainty in the path of the quantum particle.Others
The Schrödinger equationSchrödinger equation
The Schrödinger equation was formulated in 1926 by Austrian physicist Erwin Schrödinger. Used in physics , it is an equation that describes how the quantum state of a physical system changes in time....
and the heat equation
Heat equation
The heat equation is an important partial differential equation which describes the distribution of heat in a given region over time...
are also related by Wick rotation. However, there is a slight difference. Statistical mechanics n-point functions satisfy positivity whereas Wick-rotated quantum field theories satisfy reflection positivity
Schwinger function
In quantum field theory, the Wightman distributions can be analytically continued to analytic functions in Euclidean space with the domain restricted to the ordered set of points in Euclidean space with no coinciding points...
.
It is called a rotation because when we represent complex numbers as a plane
Complex plane
In mathematics, the complex plane or z-plane is a geometric representation of the complex numbers established by the real axis and the orthogonal imaginary axis...
, the multiplication of a complex number by i is equivalent to rotating the vector representing that number by an angle
Angle
In geometry, an angle is the figure formed by two rays sharing a common endpoint, called the vertex of the angle.Angles are usually presumed to be in a Euclidean plane with the circle taken for standard with regard to direction. In fact, an angle is frequently viewed as a measure of an circular arc...
of
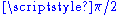 about the origin
about the originOrigin (mathematics)
In mathematics, the origin of a Euclidean space is a special point, usually denoted by the letter O, used as a fixed point of reference for the geometry of the surrounding space. In a Cartesian coordinate system, the origin is the point where the axes of the system intersect...
.
When Stephen Hawking
Stephen Hawking
Stephen William Hawking, CH, CBE, FRS, FRSA is an English theoretical physicist and cosmologist, whose scientific books and public appearances have made him an academic celebrity...
wrote about "imaginary time" in his famous book A Brief History of Time
A Brief History of Time
A Brief History of Time is a popular science book written by renown physicist Stephen Hawking and first published by the Bantam Dell Publishing Group in 1988. It became a best-seller and has sold more than 10 million copies...
, he was referring to Wick rotation.
Wick rotation also relates a QFT at a finite inverse temperature β to a statistical mechanical model over the "tube" R3×S1 with the imaginary time coordinate τ being periodic with period β.
Note, however, that the Wick rotation cannot be viewed as a rotation on a complex vector space that is equipped with the conventional norm and metric induced by the inner product, as in this case the rotation would cancel out and have no effect at all.
External links
- A Spring in Imaginary Time — a worksheet in Lagrangian mechanics illustrating how replacing length by imaginary time turns the parabola of a hanging spring into the inverted parabola of a thrown particle

