Schwinger function
Encyclopedia
In quantum field theory
, the Wightman distributions can be analytically continued
to analytic functions in Euclidean space
with the domain
restricted to the ordered set of points in Euclidean space with no coinciding points. These functions are called the Schwinger functions, named after Julian Schwinger
, and they are analytic, symmetric under the permutation of arguments (antisymmetric for fermionic field
s), Euclidean covariant and satisfy a property known as reflection positivity.
Pick any arbitrary coordinate τ and pick a test function fN with N points as its arguments. Assume fN has its support
in the "time-ordered" subset of N points with 0 < τ1 < ... < τN. Choose one such fN for each positive N, with the f's being zero for all N larger than some integer M. Given a point x, let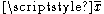
be the reflected point about the τ = 0 hyperplane
. Then,
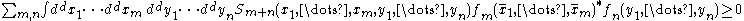
where * represents complex conjugation.
The Osterwalder-Schrader theorem states that Schwinger functions which satisfy these properties can be analytically continued into a quantum field theory
.
Euclidean path integral
s satisfy reflection positivity formally. Pick any polynomial functional
F of the field φ which doesn't depend upon the value of φ(x) for those points x whose τ coordinates are nonpositive.
Then,
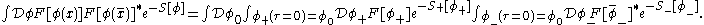
Since the action S is real and can be split into S+ which only depends on φ on the positive half-space and S− which only depends upon φ on the negative half-space and if S also happens to be invariant under the combined action of taking a reflection and complex conjugating all the fields, then the previous quantity has to be nonnegative.
Quantum field theory
Quantum field theory provides a theoretical framework for constructing quantum mechanical models of systems classically parametrized by an infinite number of dynamical degrees of freedom, that is, fields and many-body systems. It is the natural and quantitative language of particle physics and...
, the Wightman distributions can be analytically continued
Analytic continuation
In complex analysis, a branch of mathematics, analytic continuation is a technique to extend the domain of a given analytic function. Analytic continuation often succeeds in defining further values of a function, for example in a new region where an infinite series representation in terms of which...
to analytic functions in Euclidean space
Euclidean space
In mathematics, Euclidean space is the Euclidean plane and three-dimensional space of Euclidean geometry, as well as the generalizations of these notions to higher dimensions...
with the domain
Domain (mathematics)
In mathematics, the domain of definition or simply the domain of a function is the set of "input" or argument values for which the function is defined...
restricted to the ordered set of points in Euclidean space with no coinciding points. These functions are called the Schwinger functions, named after Julian Schwinger
Julian Schwinger
Julian Seymour Schwinger was an American theoretical physicist. He is best known for his work on the theory of quantum electrodynamics, in particular for developing a relativistically invariant perturbation theory, and for renormalizing QED to one loop order.Schwinger is recognized as one of the...
, and they are analytic, symmetric under the permutation of arguments (antisymmetric for fermionic field
Fermionic field
In quantum field theory, a fermionic field is a quantum field whose quanta are fermions; that is, they obey Fermi-Dirac statistics. Fermionic fields obey canonical anticommutation relations rather than the canonical commutation relations of bosonic fields....
s), Euclidean covariant and satisfy a property known as reflection positivity.
Pick any arbitrary coordinate τ and pick a test function fN with N points as its arguments. Assume fN has its support
Support (mathematics)
In mathematics, the support of a function is the set of points where the function is not zero, or the closure of that set . This concept is used very widely in mathematical analysis...
in the "time-ordered" subset of N points with 0 < τ1 < ... < τN. Choose one such fN for each positive N, with the f's being zero for all N larger than some integer M. Given a point x, let
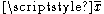be the reflected point about the τ = 0 hyperplaneHyperplane
A hyperplane is a concept in geometry. It is a generalization of the plane into a different number of dimensions.A hyperplane of an n-dimensional space is a flat subset with dimension n − 1...
. Then,
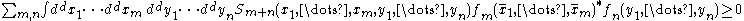
where * represents complex conjugation.
The Osterwalder-Schrader theorem states that Schwinger functions which satisfy these properties can be analytically continued into a quantum field theory
Quantum field theory
Quantum field theory provides a theoretical framework for constructing quantum mechanical models of systems classically parametrized by an infinite number of dynamical degrees of freedom, that is, fields and many-body systems. It is the natural and quantitative language of particle physics and...
.
Euclidean path integral
Functional integration
Functional integration is a collection of results in mathematics and physics where the domain of an integral is no longer a region of space, but a space of functions...
s satisfy reflection positivity formally. Pick any polynomial functional
Functional (mathematics)
In mathematics, and particularly in functional analysis, a functional is a map from a vector space into its underlying scalar field. In other words, it is a function that takes a vector as its input argument, and returns a scalar...
F of the field φ which doesn't depend upon the value of φ(x) for those points x whose τ coordinates are nonpositive.
Then,
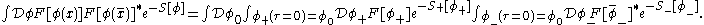
Since the action S is real and can be split into S+ which only depends on φ on the positive half-space and S− which only depends upon φ on the negative half-space and if S also happens to be invariant under the combined action of taking a reflection and complex conjugating all the fields, then the previous quantity has to be nonnegative.