Vacuum expectation value
Encyclopedia
In quantum field theory
the vacuum expectation value (also called condensate or simply VEV) of an operator
is its average, expected value
in the vacuum. The vacuum expectation value of an operator O is usually denoted by
. One of the best known examples of an observable physical effect that results from the vacuum expectation value of an operator is the Casimir effect
.
This concept is important for working with correlation functions
in quantum field theory
. It is also important in spontaneous symmetry breaking
. Examples are:
The observed Lorentz invariance of space-time allows only the formation of condensates which are Lorentz scalar
s and have vanishing charge
. Thus fermion
condensates must be of the form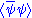
, where ψ is the fermion field. Similarly a tensor field, Gμν, can only have a scalar expectation value such as 
.
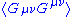In some vacua of string theory
, however, non-scalar condensates are found. If these describe our universe
, then Lorentz symmetry violation may be observable.
Quantum field theory
Quantum field theory provides a theoretical framework for constructing quantum mechanical models of systems classically parametrized by an infinite number of dynamical degrees of freedom, that is, fields and many-body systems. It is the natural and quantitative language of particle physics and...
the vacuum expectation value (also called condensate or simply VEV) of an operator
Operator (physics)
In physics, an operator is a function acting on the space of physical states. As a resultof its application on a physical state, another physical state is obtained, very often along withsome extra relevant information....
is its average, expected value
Expected value
In probability theory, the expected value of a random variable is the weighted average of all possible values that this random variable can take on...
in the vacuum. The vacuum expectation value of an operator O is usually denoted by
. One of the best known examples of an observable physical effect that results from the vacuum expectation value of an operator is the Casimir effectCasimir effect
In quantum field theory, the Casimir effect and the Casimir–Polder force are physical forces arising from a quantized field. The typical example is of two uncharged metallic plates in a vacuum, like capacitors placed a few micrometers apart, without any external electromagnetic field...
.
This concept is important for working with correlation functions
Correlation function (quantum field theory)
In quantum field theory, the matrix element computed by inserting a product of operators between two states, usually the vacuum states, is called a correlation function....
in quantum field theory
Quantum field theory
Quantum field theory provides a theoretical framework for constructing quantum mechanical models of systems classically parametrized by an infinite number of dynamical degrees of freedom, that is, fields and many-body systems. It is the natural and quantitative language of particle physics and...
. It is also important in spontaneous symmetry breaking
Spontaneous symmetry breaking
Spontaneous symmetry breaking is the process by which a system described in a theoretically symmetrical way ends up in an apparently asymmetric state....
. Examples are:
- The Higgs field has a vacuum expectation value of 246 GeVGEVGEV or GeV may stand for:*GeV or gigaelectronvolt, a unit of energy equal to billion electron volts*GEV or Grid Enabled Vehicle that is fully or partially powered by the electric grid, see plug-in electric vehicle...
. This nonzero value allows the Higgs mechanismHiggs mechanismIn particle physics, the Higgs mechanism is the process in which gauge bosons in a gauge theory can acquire non-vanishing masses through absorption of Nambu-Goldstone bosons arising in spontaneous symmetry breaking....
to work. - The chiral condensate in Quantum chromodynamicsQuantum chromodynamicsIn theoretical physics, quantum chromodynamics is a theory of the strong interaction , a fundamental force describing the interactions of the quarks and gluons making up hadrons . It is the study of the SU Yang–Mills theory of color-charged fermions...
gives a large effective mass to quarkQuarkA quark is an elementary particle and a fundamental constituent of matter. Quarks combine to form composite particles called hadrons, the most stable of which are protons and neutrons, the components of atomic nuclei. Due to a phenomenon known as color confinement, quarks are never directly...
s, and distinguishes between phases of quark matter. - The gluon condensateGluon condensateIn Quantum chromodynamics , the gluon condensate is a non-perturbative property of the QCD vacuum which could be partly responsible for giving masses to certain hadrons.If the gluon field tensor is represented as Gμν, then...
in Quantum chromodynamicsQuantum chromodynamicsIn theoretical physics, quantum chromodynamics is a theory of the strong interaction , a fundamental force describing the interactions of the quarks and gluons making up hadrons . It is the study of the SU Yang–Mills theory of color-charged fermions...
may be partly responsible for masses of hadrons.
The observed Lorentz invariance of space-time allows only the formation of condensates which are Lorentz scalar
Lorentz scalar
In physics, a Lorentz scalar is a scalar which is invariant under a Lorentz transformation. A Lorentz scalar may be generated from multiplication of vectors or tensors...
s and have vanishing charge
Charge (physics)
In physics, a charge may refer to one of many different quantities, such as the electric charge in electromagnetism or the color charge in quantum chromodynamics. Charges are associated with conserved quantum numbers.-Formal definition:...
. Thus fermion
Fermion
In particle physics, a fermion is any particle which obeys the Fermi–Dirac statistics . Fermions contrast with bosons which obey Bose–Einstein statistics....
condensates must be of the form
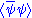, where ψ is the fermion field. Similarly a tensor field, Gμν, can only have a scalar expectation value such as 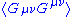.In some vacua of string theory
String theory
String theory is an active research framework in particle physics that attempts to reconcile quantum mechanics and general relativity. It is a contender for a theory of everything , a manner of describing the known fundamental forces and matter in a mathematically complete system...
, however, non-scalar condensates are found. If these describe our universe
Universe
The Universe is commonly defined as the totality of everything that exists, including all matter and energy, the planets, stars, galaxies, and the contents of intergalactic space. Definitions and usage vary and similar terms include the cosmos, the world and nature...
, then Lorentz symmetry violation may be observable.
See also
- Wightman axiomsWightman axiomsIn physics the Wightman axioms are an attempt at a mathematically rigorous formulation of quantum field theory. Arthur Wightman formulated the axioms in the early 1950s but they were first published only in 1964, after Haag-Ruelle scattering theory affirmed their significance.The axioms exist in...
and Correlation function (quantum field theory)Correlation function (quantum field theory)In quantum field theory, the matrix element computed by inserting a product of operators between two states, usually the vacuum states, is called a correlation function.... - vacuum energyVacuum energyVacuum energy is an underlying background energy that exists in space even when the space is devoid of matter . The concept of vacuum energy has been deduced from the concept of virtual particles, which is itself derived from the energy-time uncertainty principle...
or dark energyDark energyIn physical cosmology, astronomy and celestial mechanics, dark energy is a hypothetical form of energy that permeates all of space and tends to accelerate the expansion of the universe. Dark energy is the most accepted theory to explain recent observations that the universe appears to be expanding... - Spontaneous symmetry breakingSpontaneous symmetry breakingSpontaneous symmetry breaking is the process by which a system described in a theoretically symmetrical way ends up in an apparently asymmetric state....