Lorentz scalar
Encyclopedia
In physics
, a Lorentz scalar is a scalar
which is invariant
under a Lorentz transformation
. A Lorentz scalar may be generated from multiplication of vectors or tensors. While the components of vectors and tensors are in general altered by Lorentz transformations, scalars remain unchanged.
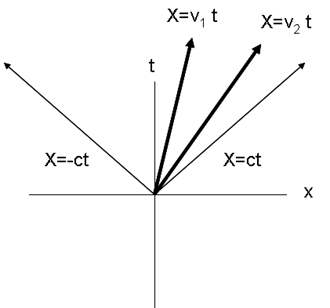In Special relativity
the location of a particle in 4-dimensional spacetime
is given by its world line
where
is the position in 3-dimensional space of the particle, 
is the velocity in 3-dimensional space and 
is the speed of light
.
The "length" of the vector is a Lorentz scalar and is given by
where
is c times the proper time as measured by a clock in the rest frame of the particle and the metric is given by
.
This is a time-like metric. Often the Minkowski metric is used in which the signs of the ones are reversed.
.
This is a space-like metric. In the Minkowski metric the space-like interval
is defined as
.
We use the Minkowski metric in the rest of this article.
The velocity in spacetime is defined as
where
.
The magnitude of the 4-velocity is a Lorentz scalar and is minus one,
.
The 4-velocity is therefore, not only a representation of the velocity in spacetime, is also a unit vector in the direction of the position of the particle in spacetime.
.
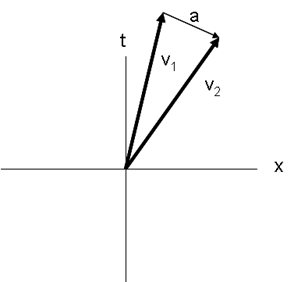
The 4-acceleration is always perpendicular to the 4-velocity
.
Therefore, we can regard acceleration in spacetime as simply a rotation of the 4-velocity. The inner product of the acceleration and the velocity is a Lorentz scalar and is zero. This rotation is simply an expression of energy conservation:
where
is the energy of a particle and 
is the 3-force on the particle.
where
is the particle rest mass, 
is the momentum in 3-space, and
is the energy of the particle.
and a 3-velocity 
. In the rest frame of the second particle the inner product of 
with 
is proportional to the energy of the first particle
where the subscript 1 indicates the first particle.
Since the relationship is true in the rest frame of the second particle, it is true in any reference frame.
, the energy of the first particle in the frame of the second particle, is a Lorentz scalar. Therefore
in any inertial reference frame, where
is still the energy of the first particle in the frame of the second particle .
.
Therefore
is a Lorentz scalar. The relationship remains true independent of the frame in which the inner product is calculated.
.
The square of the magnitude of the 3-momentum of the particle as measured in the frame of the second particle is a Lorentz scalar.
.
Physics
Physics is a natural science that involves the study of matter and its motion through spacetime, along with related concepts such as energy and force. More broadly, it is the general analysis of nature, conducted in order to understand how the universe behaves.Physics is one of the oldest academic...
, a Lorentz scalar is a scalar
Scalar (physics)
In physics, a scalar is a simple physical quantity that is not changed by coordinate system rotations or translations , or by Lorentz transformations or space-time translations . This is in contrast to a vector...
which is invariant
Invariant
Invariant and invariance may have several meanings, among which are:- Computer science :* Invariant , an Expression whose value doesn't change during program execution* A type in overriding that is neither covariant nor contravariant...
under a Lorentz transformation
Lorentz transformation
In physics, the Lorentz transformation or Lorentz-Fitzgerald transformation describes how, according to the theory of special relativity, two observers' varying measurements of space and time can be converted into each other's frames of reference. It is named after the Dutch physicist Hendrik...
. A Lorentz scalar may be generated from multiplication of vectors or tensors. While the components of vectors and tensors are in general altered by Lorentz transformations, scalars remain unchanged.
The length of a position vector
Special relativity
Special relativity is the physical theory of measurement in an inertial frame of reference proposed in 1905 by Albert Einstein in the paper "On the Electrodynamics of Moving Bodies".It generalizes Galileo's...
the location of a particle in 4-dimensional spacetime
Spacetime
In physics, spacetime is any mathematical model that combines space and time into a single continuum. Spacetime is usually interpreted with space as being three-dimensional and time playing the role of a fourth dimension that is of a different sort from the spatial dimensions...
is given by its world line
World line
In physics, the world line of an object is the unique path of that object as it travels through 4-dimensional spacetime. The concept of "world line" is distinguished from the concept of "orbit" or "trajectory" by the time dimension, and typically encompasses a large area of spacetime wherein...
where
is the position in 3-dimensional space of the particle, is the velocity in 3-dimensional space and is the speed of lightSpeed of light
The speed of light in vacuum, usually denoted by c, is a physical constant important in many areas of physics. Its value is 299,792,458 metres per second, a figure that is exact since the length of the metre is defined from this constant and the international standard for time...
.
The "length" of the vector is a Lorentz scalar and is given by
where
is c times the proper time as measured by a clock in the rest frame of the particle and the metric is given by.This is a time-like metric. Often the Minkowski metric is used in which the signs of the ones are reversed.
.This is a space-like metric. In the Minkowski metric the space-like interval
is defined as.We use the Minkowski metric in the rest of this article.
The length of a velocity vector
where
.The magnitude of the 4-velocity is a Lorentz scalar and is minus one,
.The 4-velocity is therefore, not only a representation of the velocity in spacetime, is also a unit vector in the direction of the position of the particle in spacetime.
The inner product of acceleration and velocity
The 4-acceleration is given by.The 4-acceleration is always perpendicular to the 4-velocity
.Therefore, we can regard acceleration in spacetime as simply a rotation of the 4-velocity. The inner product of the acceleration and the velocity is a Lorentz scalar and is zero. This rotation is simply an expression of energy conservation:
where
is the energy of a particle and is the 3-force on the particle.Energy, rest mass, 3-momentum, and 3-speed from 4-momentum
The 4-momentum of a particle iswhere
is the particle rest mass, is the momentum in 3-space, andis the energy of the particle.
Measurement of the energy of a particle
Consider a second particle with 4-velocity and a 3-velocity . In the rest frame of the second particle the inner product of with is proportional to the energy of the first particlewhere the subscript 1 indicates the first particle.
Since the relationship is true in the rest frame of the second particle, it is true in any reference frame.
, the energy of the first particle in the frame of the second particle, is a Lorentz scalar. Thereforein any inertial reference frame, where
is still the energy of the first particle in the frame of the second particle .Measurement of the rest mass of the particle
In the rest frame of the particle the inner product of the momentum is.Therefore
is a Lorentz scalar. The relationship remains true independent of the frame in which the inner product is calculated.Measurement of the 3-momentum of the particle
Note that.The square of the magnitude of the 3-momentum of the particle as measured in the frame of the second particle is a Lorentz scalar.
Measurement of the 3-speed of the particle
The 3-speed, in the frame of the second particle, can be constructed from two Lorentz scalars.