Hydrogen-like atom
Encyclopedia
A hydrogen-like ion is any atomic nucleus
with one electron
and thus is isoelectronic with hydrogen
. Except for the hydrogen atom
itself (which is neutral), these ions carry the positive charge e(Z-1), where Z is the atomic number
of the atom. Examples of hydrogen-like ions are He+
, Li2+
, Be3+
and B4+
. Because hydrogen-like ions are two-particle systems with an interaction depending only on the distance between the two particles, their (non-relativistic) Schrödinger equation
can be solved in analytic form. The solutions are one-electron functions and are referred to as hydrogen-like atomic orbitals.
Hydrogen-like atomic orbitals are eigenfunction
s of the one-electron angular momentum operator L and its z component Lz. The energy eigenvalues do not depend on the corresponding quantum numbers, but solely on the principal quantum number n. Hence, a hydrogen-like atomic orbital is uniquely identified by the values of: principal quantum number
n, angular momentum quantum number
l, and magnetic quantum number
m. To this must be added the two-valued spin quantum number
ms = ±½ in application of the Aufbau principle
. This principle restricts the allowed values of the four quantum numbers in electron configuration
s of more-electron atoms. In hydrogen-like atoms all degenerate orbitals of fixed n and l, m and s varying between certain values (see below) form an atomic shell
.
The Schrödinger equation of atoms or atomic ions with more than one electron has not been solved analytically, because of the computational difficulty imposed by the Coulomb interaction between the electrons. Numerical methods must be applied in order to obtain (approximate) wavefunctions or other properties from quantum mechanical calculations. Due to the spherical symmetry (of the Hamiltonian
), the total angular momentum J of an atom is a conserved quantity. Many numerical procedures start from products of atomic orbitals that are eigenfunctions of the one-electron operators L and Lz. The radial parts of these atomic orbitals are sometimes numerical tables or are sometimes Slater orbitals. By angular momentum coupling
many-electron eigenfunctions of J2 (and possibly S2) are constructed.
In quantum chemical calculations hydrogen-like atomic orbitals cannot serve as an expansion basis, because they are not complete. The non-square-integrable continuum (E > 0) states must be included to obtain a complete set, i.e., to span all of one-electron Hilbert space.
term is the potential given by Coulomb's law
:
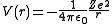
where
After writing the wave function as a product of functions: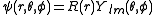
(in spherical coordinates), where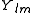
are spherical harmonics
, we arrive at the following Schrödinger equation: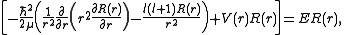
where
is, approximately, the mass
of the electron
. More accurately, it is the reduced mass
of the system consisting of the electron and the nucleus.
Different values of l give solutions with different angular momentum
, where l (a non-negative integer) is the quantum number
of the orbital angular momentum
. The magnetic quantum number
m (satisfying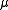
) is the (quantized) projection of the orbital angular momentum on the z-axis. See here for the steps leading to the solution of this equation.
s. It is customary to subscript the wave functions with the values of the quantum numbers they depend on. The final expression for the normalized wave function is:
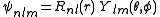
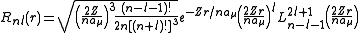
where:
parity due to angular wave function is -1 whole to the power l.
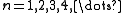
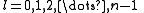
See for a group theoretical interpretation of these quantum numbers this article. Among other things,
this article gives group theoretical reasons why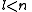
and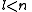 
.
L. It is a vector operator, and the eigenvalues of its square L2 ≡ Lx2 + Ly2 + Lz2 are given by:
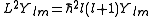
The projection of this vector onto an arbitrary direction is quantized
. If the arbitrary direction is called z, the quantization is given by:
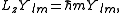
where m is restricted as described above. Note that L2 and Lz commute and have a common eigenstate, which is in accordance with Heisenberg's uncertainty principle
. Since Lx and Ly do not commute with Lz, it is not possible to find a state which is an eigenstate of all three components simultaneously. Hence the values of the x and y components are not sharp, but are given by a probability function of finite width. The fact that the x and y components are not well-determined, implies that the direction of the angular momentum vector is not well determined either, although its component along the z-axis is sharp.
These relations do not give the total angular momentum of the electron. For that, electron spin
must be included.
This quantization of angular momentum closely parallels that proposed by Niels Bohr
(see Bohr model
) in 1913, with no knowledge of wavefunctions.
interacts with the magnetic field
created by the electron movement around the nucleus, a phenomenon known as spin-orbit interaction
. When one takes this into account, the spin
and angular momentum
are no longer conserved, which can be pictured by the electron
precessing. Therefore one has to replace the quantum numbers l, m and the projection of the spin
ms by quantum numbers which represent the total angular momentum (including spin
), j and mj, as well as the quantum number
of parity
.
Atomic nucleus
The nucleus is the very dense region consisting of protons and neutrons at the center of an atom. It was discovered in 1911, as a result of Ernest Rutherford's interpretation of the famous 1909 Rutherford experiment performed by Hans Geiger and Ernest Marsden, under the direction of Rutherford. The...
with one electron
Electron
The electron is a subatomic particle with a negative elementary electric charge. It has no known components or substructure; in other words, it is generally thought to be an elementary particle. An electron has a mass that is approximately 1/1836 that of the proton...
and thus is isoelectronic with hydrogen
Hydrogen
Hydrogen is the chemical element with atomic number 1. It is represented by the symbol H. With an average atomic weight of , hydrogen is the lightest and most abundant chemical element, constituting roughly 75% of the Universe's chemical elemental mass. Stars in the main sequence are mainly...
. Except for the hydrogen atom
Hydrogen atom
A hydrogen atom is an atom of the chemical element hydrogen. The electrically neutral atom contains a single positively-charged proton and a single negatively-charged electron bound to the nucleus by the Coulomb force...
itself (which is neutral), these ions carry the positive charge e(Z-1), where Z is the atomic number
Atomic number
In chemistry and physics, the atomic number is the number of protons found in the nucleus of an atom and therefore identical to the charge number of the nucleus. It is conventionally represented by the symbol Z. The atomic number uniquely identifies a chemical element...
of the atom. Examples of hydrogen-like ions are He+
Helium
Helium is the chemical element with atomic number 2 and an atomic weight of 4.002602, which is represented by the symbol He. It is a colorless, odorless, tasteless, non-toxic, inert, monatomic gas that heads the noble gas group in the periodic table...
, Li2+
Lithium
Lithium is a soft, silver-white metal that belongs to the alkali metal group of chemical elements. It is represented by the symbol Li, and it has the atomic number 3. Under standard conditions it is the lightest metal and the least dense solid element. Like all alkali metals, lithium is highly...
, Be3+
Beryllium
Beryllium is the chemical element with the symbol Be and atomic number 4. It is a divalent element which occurs naturally only in combination with other elements in minerals. Notable gemstones which contain beryllium include beryl and chrysoberyl...
and B4+
Boron
Boron is the chemical element with atomic number 5 and the chemical symbol B. Boron is a metalloid. Because boron is not produced by stellar nucleosynthesis, it is a low-abundance element in both the solar system and the Earth's crust. However, boron is concentrated on Earth by the...
. Because hydrogen-like ions are two-particle systems with an interaction depending only on the distance between the two particles, their (non-relativistic) Schrödinger equation
Schrödinger equation
The Schrödinger equation was formulated in 1926 by Austrian physicist Erwin Schrödinger. Used in physics , it is an equation that describes how the quantum state of a physical system changes in time....
can be solved in analytic form. The solutions are one-electron functions and are referred to as hydrogen-like atomic orbitals.
Hydrogen-like atomic orbitals are eigenfunction
Eigenfunction
In mathematics, an eigenfunction of a linear operator, A, defined on some function space is any non-zero function f in that space that returns from the operator exactly as is, except for a multiplicative scaling factor. More precisely, one has...
s of the one-electron angular momentum operator L and its z component Lz. The energy eigenvalues do not depend on the corresponding quantum numbers, but solely on the principal quantum number n. Hence, a hydrogen-like atomic orbital is uniquely identified by the values of: principal quantum number
Principal quantum number
In atomic physics, the principal quantum symbolized as n is the firstof a set of quantum numbers of an atomic orbital. The principal quantum number can only have positive integer values...
n, angular momentum quantum number
Azimuthal quantum number
The azimuthal quantum number is a quantum number for an atomic orbital that determines its orbital angular momentum and describes the shape of the orbital...
l, and magnetic quantum number
Magnetic quantum number
In atomic physics, the magnetic quantum number is the third of a set of quantum numbers which describe the unique quantum state of an electron and is designated by the letter m...
m. To this must be added the two-valued spin quantum number
Spin quantum number
In atomic physics, the spin quantum number is a quantum number that parameterizes the intrinsic angular momentum of a given particle...
ms = ±½ in application of the Aufbau principle
Aufbau principle
The Aufbau principle is used to determine the electron configuration of an atom, molecule or ion. The principle postulates a hypothetical process in which an atom is "built up" by progressively adding electrons...
. This principle restricts the allowed values of the four quantum numbers in electron configuration
Electron configuration
In atomic physics and quantum chemistry, electron configuration is the arrangement of electrons of an atom, a molecule, or other physical structure...
s of more-electron atoms. In hydrogen-like atoms all degenerate orbitals of fixed n and l, m and s varying between certain values (see below) form an atomic shell
Electron shell
An electron shell may be thought of as an orbit followed by electrons around an atom's nucleus. The closest shell to the nucleus is called the "1 shell" , followed by the "2 shell" , then the "3 shell" , and so on further and further from the nucleus. The shell letters K,L,M,.....
.
The Schrödinger equation of atoms or atomic ions with more than one electron has not been solved analytically, because of the computational difficulty imposed by the Coulomb interaction between the electrons. Numerical methods must be applied in order to obtain (approximate) wavefunctions or other properties from quantum mechanical calculations. Due to the spherical symmetry (of the Hamiltonian
Hamiltonian (quantum mechanics)
In quantum mechanics, the Hamiltonian H, also Ȟ or Ĥ, is the operator corresponding to the total energy of the system. Its spectrum is the set of possible outcomes when one measures the total energy of a system...
), the total angular momentum J of an atom is a conserved quantity. Many numerical procedures start from products of atomic orbitals that are eigenfunctions of the one-electron operators L and Lz. The radial parts of these atomic orbitals are sometimes numerical tables or are sometimes Slater orbitals. By angular momentum coupling
Angular momentum coupling
In quantum mechanics, the procedure of constructing eigenstates of total angular momentum out of eigenstates of separate angular momenta is called angular momentum coupling. For instance, the orbit and spin of a single particle can interact through spin-orbit interaction, in which case the...
many-electron eigenfunctions of J2 (and possibly S2) are constructed.
In quantum chemical calculations hydrogen-like atomic orbitals cannot serve as an expansion basis, because they are not complete. The non-square-integrable continuum (E > 0) states must be included to obtain a complete set, i.e., to span all of one-electron Hilbert space.
Mathematical characterization
The atomic orbitals of hydrogen-like ions are solutions to the Schrödinger equation in a spherically symmetric potential. In this case, the potentialPotential
*In linguistics, the potential mood*The mathematical study of potentials is known as potential theory; it is the study of harmonic functions on manifolds...
term is the potential given by Coulomb's law
Coulomb's law
Coulomb's law or Coulomb's inverse-square law, is a law of physics describing the electrostatic interaction between electrically charged particles. It was first published in 1785 by French physicist Charles Augustin de Coulomb and was essential to the development of the theory of electromagnetism...
:
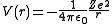
where
- ε0 is the permittivity of the vacuum,
- Z is the atomic numberAtomic numberIn chemistry and physics, the atomic number is the number of protons found in the nucleus of an atom and therefore identical to the charge number of the nucleus. It is conventionally represented by the symbol Z. The atomic number uniquely identifies a chemical element...
(number of protons in the nucleus), - e is the elementary chargeElementary chargeThe elementary charge, usually denoted as e, is the electric charge carried by a single proton, or equivalently, the absolute value of the electric charge carried by a single electron. This elementary charge is a fundamental physical constant. To avoid confusion over its sign, e is sometimes called...
(charge of an electron), - r is the distance of the electron from the nucleus.
After writing the wave function as a product of functions:
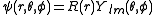
(in spherical coordinates), where
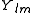are spherical harmonicsSpherical harmonics
In mathematics, spherical harmonics are the angular portion of a set of solutions to Laplace's equation. Represented in a system of spherical coordinates, Laplace's spherical harmonics Y_\ell^m are a specific set of spherical harmonics that forms an orthogonal system, first introduced by Pierre...
, we arrive at the following Schrödinger equation:
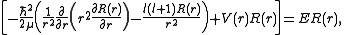
where
is, approximately, the massMass
Mass can be defined as a quantitive measure of the resistance an object has to change in its velocity.In physics, mass commonly refers to any of the following three properties of matter, which have been shown experimentally to be equivalent:...
of the electron
Electron
The electron is a subatomic particle with a negative elementary electric charge. It has no known components or substructure; in other words, it is generally thought to be an elementary particle. An electron has a mass that is approximately 1/1836 that of the proton...
. More accurately, it is the reduced mass
Reduced mass
Reduced mass is the "effective" inertial mass appearing in the two-body problem of Newtonian mechanics. This is a quantity with the unit of mass, which allows the two-body problem to be solved as if it were a one-body problem. Note however that the mass determining the gravitational force is not...
of the system consisting of the electron and the nucleus.
Different values of l give solutions with different angular momentum
Angular momentum
In physics, angular momentum, moment of momentum, or rotational momentum is a conserved vector quantity that can be used to describe the overall state of a physical system...
, where l (a non-negative integer) is the quantum number
Quantum number
Quantum numbers describe values of conserved quantities in the dynamics of the quantum system. Perhaps the most peculiar aspect of quantum mechanics is the quantization of observable quantities. This is distinguished from classical mechanics where the values can range continuously...
of the orbital angular momentum
Angular momentum
In physics, angular momentum, moment of momentum, or rotational momentum is a conserved vector quantity that can be used to describe the overall state of a physical system...
. The magnetic quantum number
Magnetic quantum number
In atomic physics, the magnetic quantum number is the third of a set of quantum numbers which describe the unique quantum state of an electron and is designated by the letter m...
m (satisfying
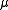) is the (quantized) projection of the orbital angular momentum on the z-axis. See here for the steps leading to the solution of this equation.Non-relativistic wavefunction and energy
In addition to l and m, a third integer n > 0, emerges from the boundary conditions placed on R. The functions R and Y that solve the equations above depend on the values of these integers, called quantum numberQuantum number
Quantum numbers describe values of conserved quantities in the dynamics of the quantum system. Perhaps the most peculiar aspect of quantum mechanics is the quantization of observable quantities. This is distinguished from classical mechanics where the values can range continuously...
s. It is customary to subscript the wave functions with the values of the quantum numbers they depend on. The final expression for the normalized wave function is:
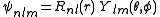
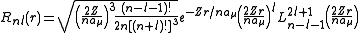
where:
-
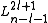are the generalized Laguerre polynomialsLaguerre polynomialsIn mathematics, the Laguerre polynomials, named after Edmond Laguerre ,are the canonical solutions of Laguerre's equation:x\,y + \,y' + n\,y = 0\,which is a second-order linear differential equation....
in the definition given hereLaguerre polynomialsIn mathematics, the Laguerre polynomials, named after Edmond Laguerre ,are the canonical solutions of Laguerre's equation:x\,y + \,y' + n\,y = 0\,which is a second-order linear differential equation....
. -
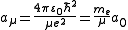
- Here,
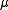is the reduced mass of the nucleus-electron system, that is, 
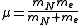where 
is the mass of the nucleus. Typically, the nucleus is much more massive than the electron, so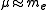 
.
-
. -
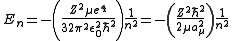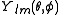function is a spherical harmonicSpherical HarmonicSpherical Harmonic is a science fiction novel from the Saga of the Skolian Empire by Catherine Asaro. It tells the story of Dyhianna Selei , the Ruby Pharaoh of the Skolian Imperialate, as she strives to reform her government and reunite her family in the aftermath of a devastating interstellar...
.
-
parity due to angular wave function is -1 whole to the power l.
Quantum numbers
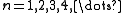
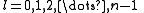
The quantum numbers n, l and m are integers and can have the following values:See for a group theoretical interpretation of these quantum numbers this article. Among other things,
this article gives group theoretical reasons why
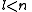and 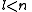.Angular momentum
Each atomic orbital is associated with an angular momentumAngular momentum
In physics, angular momentum, moment of momentum, or rotational momentum is a conserved vector quantity that can be used to describe the overall state of a physical system...
L. It is a vector operator, and the eigenvalues of its square L2 ≡ Lx2 + Ly2 + Lz2 are given by:
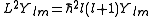
The projection of this vector onto an arbitrary direction is quantized
Quantization (physics)
In physics, quantization is the process of explaining a classical understanding of physical phenomena in terms of a newer understanding known as "quantum mechanics". It is a procedure for constructing a quantum field theory starting from a classical field theory. This is a generalization of the...
. If the arbitrary direction is called z, the quantization is given by:
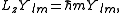
where m is restricted as described above. Note that L2 and Lz commute and have a common eigenstate, which is in accordance with Heisenberg's uncertainty principle
Uncertainty principle
In quantum mechanics, the Heisenberg uncertainty principle states a fundamental limit on the accuracy with which certain pairs of physical properties of a particle, such as position and momentum, can be simultaneously known...
. Since Lx and Ly do not commute with Lz, it is not possible to find a state which is an eigenstate of all three components simultaneously. Hence the values of the x and y components are not sharp, but are given by a probability function of finite width. The fact that the x and y components are not well-determined, implies that the direction of the angular momentum vector is not well determined either, although its component along the z-axis is sharp.
These relations do not give the total angular momentum of the electron. For that, electron spin
Spin (physics)
In quantum mechanics and particle physics, spin is a fundamental characteristic property of elementary particles, composite particles , and atomic nuclei.It is worth noting that the intrinsic property of subatomic particles called spin and discussed in this article, is related in some small ways,...
must be included.
This quantization of angular momentum closely parallels that proposed by Niels Bohr
Niels Bohr
Niels Henrik David Bohr was a Danish physicist who made foundational contributions to understanding atomic structure and quantum mechanics, for which he received the Nobel Prize in Physics in 1922. Bohr mentored and collaborated with many of the top physicists of the century at his institute in...
(see Bohr model
Bohr model
In atomic physics, the Bohr model, introduced by Niels Bohr in 1913, depicts the atom as a small, positively charged nucleus surrounded by electrons that travel in circular orbits around the nucleus—similar in structure to the solar system, but with electrostatic forces providing attraction,...
) in 1913, with no knowledge of wavefunctions.
Including spin-orbit interaction
In a real atom the spinSpin (physics)
In quantum mechanics and particle physics, spin is a fundamental characteristic property of elementary particles, composite particles , and atomic nuclei.It is worth noting that the intrinsic property of subatomic particles called spin and discussed in this article, is related in some small ways,...
interacts with the magnetic field
Magnetic field
A magnetic field is a mathematical description of the magnetic influence of electric currents and magnetic materials. The magnetic field at any given point is specified by both a direction and a magnitude ; as such it is a vector field.Technically, a magnetic field is a pseudo vector;...
created by the electron movement around the nucleus, a phenomenon known as spin-orbit interaction
Spin-orbit interaction
In quantum physics, the spin-orbit interaction is any interaction of a particle's spin with its motion. The first and best known example of this is that spin-orbit interaction causes shifts in an electron's atomic energy levels due to electromagnetic interaction between the electron's spin and...
. When one takes this into account, the spin
Spin (physics)
In quantum mechanics and particle physics, spin is a fundamental characteristic property of elementary particles, composite particles , and atomic nuclei.It is worth noting that the intrinsic property of subatomic particles called spin and discussed in this article, is related in some small ways,...
and angular momentum
Angular momentum
In physics, angular momentum, moment of momentum, or rotational momentum is a conserved vector quantity that can be used to describe the overall state of a physical system...
are no longer conserved, which can be pictured by the electron
Electron
The electron is a subatomic particle with a negative elementary electric charge. It has no known components or substructure; in other words, it is generally thought to be an elementary particle. An electron has a mass that is approximately 1/1836 that of the proton...
precessing. Therefore one has to replace the quantum numbers l, m and the projection of the spin
Spin (physics)
In quantum mechanics and particle physics, spin is a fundamental characteristic property of elementary particles, composite particles , and atomic nuclei.It is worth noting that the intrinsic property of subatomic particles called spin and discussed in this article, is related in some small ways,...
ms by quantum numbers which represent the total angular momentum (including spin
Spin (physics)
In quantum mechanics and particle physics, spin is a fundamental characteristic property of elementary particles, composite particles , and atomic nuclei.It is worth noting that the intrinsic property of subatomic particles called spin and discussed in this article, is related in some small ways,...
), j and mj, as well as the quantum number
Quantum number
Quantum numbers describe values of conserved quantities in the dynamics of the quantum system. Perhaps the most peculiar aspect of quantum mechanics is the quantization of observable quantities. This is distinguished from classical mechanics where the values can range continuously...
of parity
Parity (physics)
In physics, a parity transformation is the flip in the sign of one spatial coordinate. In three dimensions, it is also commonly described by the simultaneous flip in the sign of all three spatial coordinates:...
.