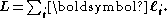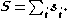Angular momentum coupling
Encyclopedia
In quantum mechanics
, the procedure of constructing eigenstates of total angular momentum out of eigenstates of separate angular momenta is called angular momentum coupling. For instance, the orbit and spin of a single particle can interact through spin-orbit interaction
, in which case the complete physical picture must include spin-orbit coupling. Or two charged particles, each with a well-defined angular momentum, may interact by Coulomb forces, in which case coupling of the two one-particle angular momenta to a total angular momentum is a useful step in the solution of the two-particle Schrödinger equation
.
In both cases the separate angular momenta are no longer constants of motion, but the sum of the two angular momenta usually still is. Angular momentum coupling in atoms is of importance in atomic spectroscopy
. Angular momentum coupling of electron spins is of importance in quantum chemistry
. Also in the nuclear shell model angular momentum coupling is ubiquitous.
In astronomy
, spin-orbit coupling reflects the general law of conservation of angular momentum, which holds for celestial systems as well. In simple cases, the direction of the angular momentum
vector is neglected, and the spin-orbit coupling is the ratio between the frequency with which a planet
or other celestial body
spins about its own axis to that with which it orbits another body. This is more commonly known as orbital resonance
. Often, the underlying physical effects are tidal forces
.
is a property of a physical system that is a constant of motion
(is time-independent and well-defined) in two situations: (i) The system experiences a spherically symmetric potential field. (ii) The system moves (in quantum mechanical sense) in isotropic space. In both cases the angular momentum operator commutes with the Hamiltonian
of the system. By Heisenberg's uncertainty relation this means that the angular momentum can assume a sharp value simultaneously with the energy (eigenvalue of the Hamiltonian).
An example of the first situation is an atom whose electrons only feel the Coulomb field of its nucleus. If we ignore the electron-electron interaction (and other small interactions such as spin-orbit coupling), the orbital angular momentum l of each electron commutes with the total Hamiltonian. In this model the atomic Hamiltonian is a sum of kinetic energies of the electrons and the spherically symmetric electron-nucleus interactions. The individual electron angular momenta l(i) commute with this Hamiltonian. That is, they are conserved properties of this approximate model of the atom.
An example of the second situation is a rigid rotor
moving in field-free space. A rigid rotor has a well-defined, time-independent, angular momentum.
These two situations originate in classical mechanics. The third kind of conserved angular momentum, associated with spin
, does not have a classical counterpart. However, all rules of angular momentum coupling apply to spin as well.
In general the conservation of angular momentum implies full rotational symmetry
(described by the groups SO(3) and SU(2)) and, conversely, spherical symmetry implies conservation of angular momentum. If two or more physical systems have conserved angular momenta, it can be useful to add these momenta to a total angular momentum of the combined system—a conserved property of the total system.
The building of eigenstates of the total conserved angular momentum from the angular momentum eigenstates of the individual subsystems is referred to as angular momentum coupling.
Application of angular momentum coupling is useful when there is an interaction between subsystems that, without interaction, would have conserved angular momentum. By the very interaction the spherical symmetry of the subsystems is broken, but the angular momentum of the total system remains a constant of motion. Use of the latter fact is helpful in the solution of the Schrödinger equation.
As an example we consider two electrons, 1 and 2, in an atom (say the helium atom). If there is no electron-electron interaction, but only electron-nucleus interaction, the two electrons can be rotated around the nucleus independently of each other; nothing happens to their energy. Both operators, l(1) and l(2), are conserved.
However, if we switch on the electron-electron interaction that depends on the distance d(1,2) between the electrons, then only a simultaneous
and equal rotation of the two electrons will leave d(1,2) invariant. In such a case neither
l(1) nor l(2) is a constant of motion in general, but L = l(1) + l(2)
is. Given the eigenstates of l(1) and l(2), the construction of eigenstates of L (which still is conserved) is the coupling of the angular momenta of electrons 1 and 2.
In quantum mechanics
, coupling also exists between angular momenta belonging to different Hilbert space
s of a single object, e.g. its spin
and its orbital angular momentum
.
Reiterating slightly differently the above: one expands the quantum states of composed systems (i.e. made of subunits like two hydrogen atom
s or two electron
s) in basis sets
which are made of tensor product
s of quantum states which in turn describe the subsystems individually. We assume that the states of the subsystems can be chosen as eigenstates of their angular momentum operators (and of their component along any arbitrary z axis). The subsystems are therefore correctly described by a set of l, m quantum number
s (see angular momentum
for details). When there is interaction among the subsystems, the total Hamiltonian contains terms that do not commute with the angular operators acting on the subsystems only. However, these terms do commute with the total angular momentum operator. Sometimes one refers to the non-commuting interaction terms in the Hamiltonian as angular momentum coupling terms, because they necessitate the angular momentum coupling.
is well described by the theory of quantum mechanics
, in which each particle has an intrinsic angular momentum called spin
and specific configurations (of e.g. electrons in an atom) are described by a set of quantum numbers. Collections of particles also have angular momenta and corresponding quantum numbers, and under different circumstances the angular momenta of the parts add in different ways to form the angular momentum of the whole. Angular momentum coupling is a category including some of the ways that subatomic particles can interact with each other.
In atomic physics
, spin-orbit coupling, also known as spin-pairing, describes a weak magnetic interaction, or coupling
, of the particle spin
and the orbital motion
of this particle, e.g. the electron
spin and its motion around an atom
ic nucleus
. One of its effects is to separate the energy of internal states of the atom, e.g. spin-aligned and spin-antialigned that would otherwise be identical in energy. This interaction is responsible for many of the details of atomic structure.
In the macroscopic
world of orbital mechanics
, the term spin-orbit coupling is sometimes used in the same sense as spin-orbital resonance.
–Saunders coupling or LS coupling. Then S and L add together and form a total angular momentum J:
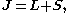
where
and
This is an approximation which is good as long as any external magnetic fields are weak. In larger magnetic fields, these two momenta decouple, giving rise to a different splitting pattern in the energy levels (the Paschen–Back effect.), and the size of LS coupling term becomes small.
For an extensive example on how LS-coupling is practically applied, see the article on term symbol
s.
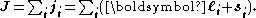
This description, facilitating calculation of this kind of interaction, is known as jj coupling.
and Dipolar coupling in NMR spectroscopy
Spin-spin coupling is the coupling of the intrinsic angular momentum (spin
) of different particles.
Such coupling between pairs of nuclear spins is an important feature of nuclear magnetic resonance
(NMR) spectroscopy as it can
provide detailed information about the structure and conformation of molecules.
Spin-spin coupling between nuclear spin and electronic spin is responsible for hyperfine structure
in atomic spectra.
s are used to represent the states and spectral transitions of atoms, they are found from coupling of angular momenta mentioned above. When the state of an atom has been specified with a term symbol, the allowed transitions can be found through selection rule
s by considering which transitions would conserve angular momentum
. A photon
has spin 1, and when there is a transition with emission or absorption of a photon the atom will need to change state to conserve angular momentum. The term symbol selection rules are. ΔS = 0, ΔL = 0, ±1, Δl = ± 1, ΔJ = 0, ±1
The expression "term symbol" is derived from the "term series" associated with the Rydberg states of an atom and their energy levels. In the Rydberg formula
the frequency or wave number of the light emitted by a hydrogen-like atom is proportional to the difference between the two terms of a transition. The series known to early spectroscopy
were designated sharp, principal, diffuse and fundamental and consequently the letters S, P, D, and F were used to represent the orbital angular momentum states of an atom.
, which assumes an average potential rather than a central Coulombic potential, the nucleons that go into the l + s and l − s nuclear states are considered degenerate within each orbital (e.g. The 2p3/2 contains four nucleons, all of the same energy. Higher in energy is the 2p1/2 which contains two equal-energy nucleons).
Quantum mechanics
Quantum mechanics, also known as quantum physics or quantum theory, is a branch of physics providing a mathematical description of much of the dual particle-like and wave-like behavior and interactions of energy and matter. It departs from classical mechanics primarily at the atomic and subatomic...
, the procedure of constructing eigenstates of total angular momentum out of eigenstates of separate angular momenta is called angular momentum coupling. For instance, the orbit and spin of a single particle can interact through spin-orbit interaction
Spin-orbit interaction
In quantum physics, the spin-orbit interaction is any interaction of a particle's spin with its motion. The first and best known example of this is that spin-orbit interaction causes shifts in an electron's atomic energy levels due to electromagnetic interaction between the electron's spin and...
, in which case the complete physical picture must include spin-orbit coupling. Or two charged particles, each with a well-defined angular momentum, may interact by Coulomb forces, in which case coupling of the two one-particle angular momenta to a total angular momentum is a useful step in the solution of the two-particle Schrödinger equation
Schrödinger equation
The Schrödinger equation was formulated in 1926 by Austrian physicist Erwin Schrödinger. Used in physics , it is an equation that describes how the quantum state of a physical system changes in time....
.
In both cases the separate angular momenta are no longer constants of motion, but the sum of the two angular momenta usually still is. Angular momentum coupling in atoms is of importance in atomic spectroscopy
Spectroscopy
Spectroscopy is the study of the interaction between matter and radiated energy. Historically, spectroscopy originated through the study of visible light dispersed according to its wavelength, e.g., by a prism. Later the concept was expanded greatly to comprise any interaction with radiative...
. Angular momentum coupling of electron spins is of importance in quantum chemistry
Quantum chemistry
Quantum chemistry is a branch of chemistry whose primary focus is the application of quantum mechanics in physical models and experiments of chemical systems...
. Also in the nuclear shell model angular momentum coupling is ubiquitous.
In astronomy
Astronomy
Astronomy is a natural science that deals with the study of celestial objects and phenomena that originate outside the atmosphere of Earth...
, spin-orbit coupling reflects the general law of conservation of angular momentum, which holds for celestial systems as well. In simple cases, the direction of the angular momentum
Angular momentum
In physics, angular momentum, moment of momentum, or rotational momentum is a conserved vector quantity that can be used to describe the overall state of a physical system...
vector is neglected, and the spin-orbit coupling is the ratio between the frequency with which a planet
Planet
A planet is a celestial body orbiting a star or stellar remnant that is massive enough to be rounded by its own gravity, is not massive enough to cause thermonuclear fusion, and has cleared its neighbouring region of planetesimals.The term planet is ancient, with ties to history, science,...
or other celestial body
Celestial Body
Celestial Body is a Croatian film directed by Lukas Nola. It was released in 2000....
spins about its own axis to that with which it orbits another body. This is more commonly known as orbital resonance
Orbital resonance
In celestial mechanics, an orbital resonance occurs when two orbiting bodies exert a regular, periodic gravitational influence on each other, usually due to their orbital periods being related by a ratio of two small integers. Orbital resonances greatly enhance the mutual gravitational influence of...
. Often, the underlying physical effects are tidal forces
Tide
Tides are the rise and fall of sea levels caused by the combined effects of the gravitational forces exerted by the moon and the sun and the rotation of the Earth....
.
General theory and detailed origin
Conservation of angular momentum is the principle that the total angular momentum of a system has a constant magnitude and direction if the system is subjected to no external force. Angular momentumAngular momentum
In physics, angular momentum, moment of momentum, or rotational momentum is a conserved vector quantity that can be used to describe the overall state of a physical system...
is a property of a physical system that is a constant of motion
Constant of motion
In mechanics, a constant of motion is a quantity that is conserved throughout the motion, imposing in effect a constraint on the motion. However, it is a mathematical constraint, the natural consequence of the equations of motion, rather than a physical constraint...
(is time-independent and well-defined) in two situations: (i) The system experiences a spherically symmetric potential field. (ii) The system moves (in quantum mechanical sense) in isotropic space. In both cases the angular momentum operator commutes with the Hamiltonian
Hamiltonian (quantum mechanics)
In quantum mechanics, the Hamiltonian H, also Ȟ or Ĥ, is the operator corresponding to the total energy of the system. Its spectrum is the set of possible outcomes when one measures the total energy of a system...
of the system. By Heisenberg's uncertainty relation this means that the angular momentum can assume a sharp value simultaneously with the energy (eigenvalue of the Hamiltonian).
An example of the first situation is an atom whose electrons only feel the Coulomb field of its nucleus. If we ignore the electron-electron interaction (and other small interactions such as spin-orbit coupling), the orbital angular momentum l of each electron commutes with the total Hamiltonian. In this model the atomic Hamiltonian is a sum of kinetic energies of the electrons and the spherically symmetric electron-nucleus interactions. The individual electron angular momenta l(i) commute with this Hamiltonian. That is, they are conserved properties of this approximate model of the atom.
An example of the second situation is a rigid rotor
Rigid rotor
The rigid rotor is a mechanical model that is used to explain rotating systems.An arbitrary rigid rotor is a 3-dimensional rigid object, such as a top. To orient such an object in space three angles are required. A special rigid rotor is the linear rotor which isa 2-dimensional object, requiring...
moving in field-free space. A rigid rotor has a well-defined, time-independent, angular momentum.
These two situations originate in classical mechanics. The third kind of conserved angular momentum, associated with spin
Spin (physics)
In quantum mechanics and particle physics, spin is a fundamental characteristic property of elementary particles, composite particles , and atomic nuclei.It is worth noting that the intrinsic property of subatomic particles called spin and discussed in this article, is related in some small ways,...
, does not have a classical counterpart. However, all rules of angular momentum coupling apply to spin as well.
In general the conservation of angular momentum implies full rotational symmetry
(described by the groups SO(3) and SU(2)) and, conversely, spherical symmetry implies conservation of angular momentum. If two or more physical systems have conserved angular momenta, it can be useful to add these momenta to a total angular momentum of the combined system—a conserved property of the total system.
The building of eigenstates of the total conserved angular momentum from the angular momentum eigenstates of the individual subsystems is referred to as angular momentum coupling.
Application of angular momentum coupling is useful when there is an interaction between subsystems that, without interaction, would have conserved angular momentum. By the very interaction the spherical symmetry of the subsystems is broken, but the angular momentum of the total system remains a constant of motion. Use of the latter fact is helpful in the solution of the Schrödinger equation.
As an example we consider two electrons, 1 and 2, in an atom (say the helium atom). If there is no electron-electron interaction, but only electron-nucleus interaction, the two electrons can be rotated around the nucleus independently of each other; nothing happens to their energy. Both operators, l(1) and l(2), are conserved.
However, if we switch on the electron-electron interaction that depends on the distance d(1,2) between the electrons, then only a simultaneous
and equal rotation of the two electrons will leave d(1,2) invariant. In such a case neither
l(1) nor l(2) is a constant of motion in general, but L = l(1) + l(2)
is. Given the eigenstates of l(1) and l(2), the construction of eigenstates of L (which still is conserved) is the coupling of the angular momenta of electrons 1 and 2.
In quantum mechanics
Quantum mechanics
Quantum mechanics, also known as quantum physics or quantum theory, is a branch of physics providing a mathematical description of much of the dual particle-like and wave-like behavior and interactions of energy and matter. It departs from classical mechanics primarily at the atomic and subatomic...
, coupling also exists between angular momenta belonging to different Hilbert space
Hilbert space
The mathematical concept of a Hilbert space, named after David Hilbert, generalizes the notion of Euclidean space. It extends the methods of vector algebra and calculus from the two-dimensional Euclidean plane and three-dimensional space to spaces with any finite or infinite number of dimensions...
s of a single object, e.g. its spin
Spin (physics)
In quantum mechanics and particle physics, spin is a fundamental characteristic property of elementary particles, composite particles , and atomic nuclei.It is worth noting that the intrinsic property of subatomic particles called spin and discussed in this article, is related in some small ways,...
and its orbital angular momentum
Angular momentum
In physics, angular momentum, moment of momentum, or rotational momentum is a conserved vector quantity that can be used to describe the overall state of a physical system...
.
Reiterating slightly differently the above: one expands the quantum states of composed systems (i.e. made of subunits like two hydrogen atom
Hydrogen atom
A hydrogen atom is an atom of the chemical element hydrogen. The electrically neutral atom contains a single positively-charged proton and a single negatively-charged electron bound to the nucleus by the Coulomb force...
s or two electron
Electron
The electron is a subatomic particle with a negative elementary electric charge. It has no known components or substructure; in other words, it is generally thought to be an elementary particle. An electron has a mass that is approximately 1/1836 that of the proton...
s) in basis sets
Basis (linear algebra)
In linear algebra, a basis is a set of linearly independent vectors that, in a linear combination, can represent every vector in a given vector space or free module, or, more simply put, which define a "coordinate system"...
which are made of tensor product
Tensor product
In mathematics, the tensor product, denoted by ⊗, may be applied in different contexts to vectors, matrices, tensors, vector spaces, algebras, topological vector spaces, and modules, among many other structures or objects. In each case the significance of the symbol is the same: the most general...
s of quantum states which in turn describe the subsystems individually. We assume that the states of the subsystems can be chosen as eigenstates of their angular momentum operators (and of their component along any arbitrary z axis). The subsystems are therefore correctly described by a set of l, m quantum number
Quantum number
Quantum numbers describe values of conserved quantities in the dynamics of the quantum system. Perhaps the most peculiar aspect of quantum mechanics is the quantization of observable quantities. This is distinguished from classical mechanics where the values can range continuously...
s (see angular momentum
Angular momentum
In physics, angular momentum, moment of momentum, or rotational momentum is a conserved vector quantity that can be used to describe the overall state of a physical system...
for details). When there is interaction among the subsystems, the total Hamiltonian contains terms that do not commute with the angular operators acting on the subsystems only. However, these terms do commute with the total angular momentum operator. Sometimes one refers to the non-commuting interaction terms in the Hamiltonian as angular momentum coupling terms, because they necessitate the angular momentum coupling.
Spin-orbit coupling
The behavior of atoms and smaller particlesSubatomic particle
In physics or chemistry, subatomic particles are the smaller particles composing nucleons and atoms. There are two types of subatomic particles: elementary particles, which are not made of other particles, and composite particles...
is well described by the theory of quantum mechanics
Quantum mechanics
Quantum mechanics, also known as quantum physics or quantum theory, is a branch of physics providing a mathematical description of much of the dual particle-like and wave-like behavior and interactions of energy and matter. It departs from classical mechanics primarily at the atomic and subatomic...
, in which each particle has an intrinsic angular momentum called spin
Spin (physics)
In quantum mechanics and particle physics, spin is a fundamental characteristic property of elementary particles, composite particles , and atomic nuclei.It is worth noting that the intrinsic property of subatomic particles called spin and discussed in this article, is related in some small ways,...
and specific configurations (of e.g. electrons in an atom) are described by a set of quantum numbers. Collections of particles also have angular momenta and corresponding quantum numbers, and under different circumstances the angular momenta of the parts add in different ways to form the angular momentum of the whole. Angular momentum coupling is a category including some of the ways that subatomic particles can interact with each other.
In atomic physics
Atomic physics
Atomic physics is the field of physics that studies atoms as an isolated system of electrons and an atomic nucleus. It is primarily concerned with the arrangement of electrons around the nucleus and...
, spin-orbit coupling, also known as spin-pairing, describes a weak magnetic interaction, or coupling
Coupling (physics)
In physics, two systems are coupled if they are interacting with each other. Of special interest is the coupling of two vibratory systems by means of springs or magnetic fields, etc...
, of the particle spin
Spin (physics)
In quantum mechanics and particle physics, spin is a fundamental characteristic property of elementary particles, composite particles , and atomic nuclei.It is worth noting that the intrinsic property of subatomic particles called spin and discussed in this article, is related in some small ways,...
and the orbital motion
Orbital motion (quantum)
Electrons don’t actually move in their orbitals. When quantum mechanics refer to “electron orbital motion” they are actually referring to the spatial wave function of the electron....
of this particle, e.g. the electron
Electron
The electron is a subatomic particle with a negative elementary electric charge. It has no known components or substructure; in other words, it is generally thought to be an elementary particle. An electron has a mass that is approximately 1/1836 that of the proton...
spin and its motion around an atom
Atom
The atom is a basic unit of matter that consists of a dense central nucleus surrounded by a cloud of negatively charged electrons. The atomic nucleus contains a mix of positively charged protons and electrically neutral neutrons...
ic nucleus
Atomic nucleus
The nucleus is the very dense region consisting of protons and neutrons at the center of an atom. It was discovered in 1911, as a result of Ernest Rutherford's interpretation of the famous 1909 Rutherford experiment performed by Hans Geiger and Ernest Marsden, under the direction of Rutherford. The...
. One of its effects is to separate the energy of internal states of the atom, e.g. spin-aligned and spin-antialigned that would otherwise be identical in energy. This interaction is responsible for many of the details of atomic structure.
In the macroscopic
Macroscopic
The macroscopic scale is the length scale on which objects or processes are of a size which is measurable and observable by the naked eye.When applied to phenomena and abstract objects, the macroscopic scale describes existence in the world as we perceive it, often in contrast to experiences or...
world of orbital mechanics
Astrodynamics
Orbital mechanics or astrodynamics is the application of ballistics and celestial mechanics to the practical problems concerning the motion of rockets and other spacecraft. The motion of these objects is usually calculated from Newton's laws of motion and Newton's law of universal gravitation. It...
, the term spin-orbit coupling is sometimes used in the same sense as spin-orbital resonance.
LS coupling
In light atoms (generally Z < 30), electron spins si interact among themselves so they combine to form a total spin angular momentum S. The same happens with orbital angular momenta ℓi, forming a total orbital angular momentum L. The interaction between the quantum numbers L and S is called RussellHenry Norris Russell
Henry Norris Russell was an American astronomer who, along with Ejnar Hertzsprung, developed the Hertzsprung–Russell diagram . In 1923, working with Frederick Saunders, he developed Russell–Saunders coupling which is also known as LS coupling.-Biography:Russell was born in 1877 in Oyster Bay, New...
–Saunders coupling or LS coupling. Then S and L add together and form a total angular momentum J:
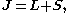
where
and
This is an approximation which is good as long as any external magnetic fields are weak. In larger magnetic fields, these two momenta decouple, giving rise to a different splitting pattern in the energy levels (the Paschen–Back effect.), and the size of LS coupling term becomes small.
For an extensive example on how LS-coupling is practically applied, see the article on term symbol
Term symbol
In quantum mechanics, the Russell-Saunders term symbol is an abbreviated description of the angular momentum quantum numbers in a multi-electron atom. It is related with the energy level of a given electron configuration. LS coupling is assumed...
s.
jj coupling
In heavier atoms the situation is different. In atoms with bigger nuclear charges, spin-orbit interactions are frequently as large as or larger than spin-spin interactions or orbit-orbit interactions. In this situation, each orbital angular momentum ℓi tends to combine with the corresponding individual spin angular momentum si, originating an individual total angular momentum ji. These then add up to form the total angular momentum J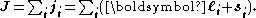
This description, facilitating calculation of this kind of interaction, is known as jj coupling.
Spin-spin coupling
See also: J-couplingJ-coupling
J-coupling is the coupling between two nuclear spins due to the influence of bonding electrons on the magnetic field running between the two nuclei. J-coupling contains information about dihedral angles, which can be estimated using the Karplus equation...
and Dipolar coupling in NMR spectroscopy
Spin-spin coupling is the coupling of the intrinsic angular momentum (spin
Spin (physics)
In quantum mechanics and particle physics, spin is a fundamental characteristic property of elementary particles, composite particles , and atomic nuclei.It is worth noting that the intrinsic property of subatomic particles called spin and discussed in this article, is related in some small ways,...
) of different particles.
Such coupling between pairs of nuclear spins is an important feature of nuclear magnetic resonance
Nuclear magnetic resonance
Nuclear magnetic resonance is a physical phenomenon in which magnetic nuclei in a magnetic field absorb and re-emit electromagnetic radiation...
(NMR) spectroscopy as it can
provide detailed information about the structure and conformation of molecules.
Spin-spin coupling between nuclear spin and electronic spin is responsible for hyperfine structure
Hyperfine structure
The term hyperfine structure refers to a collection of different effects leading to small shifts and splittings in the energy levels of atoms, molecules and ions. The name is a reference to the fine structure which results from the interaction between the magnetic moments associated with electron...
in atomic spectra.
Term symbols
Term symbolTerm symbol
In quantum mechanics, the Russell-Saunders term symbol is an abbreviated description of the angular momentum quantum numbers in a multi-electron atom. It is related with the energy level of a given electron configuration. LS coupling is assumed...
s are used to represent the states and spectral transitions of atoms, they are found from coupling of angular momenta mentioned above. When the state of an atom has been specified with a term symbol, the allowed transitions can be found through selection rule
Selection rule
In physics and chemistry a selection rule, or transition rule, formally constrains the possible transitions of a system from one state to another. Selection rules have been derived for electronic, vibrational, and rotational transitions...
s by considering which transitions would conserve angular momentum
Angular momentum
In physics, angular momentum, moment of momentum, or rotational momentum is a conserved vector quantity that can be used to describe the overall state of a physical system...
. A photon
Photon
In physics, a photon is an elementary particle, the quantum of the electromagnetic interaction and the basic unit of light and all other forms of electromagnetic radiation. It is also the force carrier for the electromagnetic force...
has spin 1, and when there is a transition with emission or absorption of a photon the atom will need to change state to conserve angular momentum. The term symbol selection rules are. ΔS = 0, ΔL = 0, ±1, Δl = ± 1, ΔJ = 0, ±1
The expression "term symbol" is derived from the "term series" associated with the Rydberg states of an atom and their energy levels. In the Rydberg formula
Rydberg formula
The Rydberg formula is used in atomic physics to describe the wavelengths of spectral lines of many chemical elements. It was formulated by the Swedish physicist Johannes Rydberg, and presented on November 5, 1888.-History:...
the frequency or wave number of the light emitted by a hydrogen-like atom is proportional to the difference between the two terms of a transition. The series known to early spectroscopy
Atomic spectral line
In physics, atomic spectral lines are of two types:* An emission line is formed when an electron makes a transition from a particular discrete energy level of an atom, to a lower energy state, emitting a photon of a particular energy and wavelength...
were designated sharp, principal, diffuse and fundamental and consequently the letters S, P, D, and F were used to represent the orbital angular momentum states of an atom.
Relativistic effects
In very heavy atoms, relativistic shifting of the energies of the electron energy levels accentuates spin-orbit coupling effect. Thus, for example, uranium molecular orbital diagrams must directly incorporate relativistic symbols when considering interactions with other atoms.Nuclear coupling
In atomic nuclei, the spin-orbit interaction is much stronger than for atomic electrons, and is incorporated directly into the nuclear shell model. In addition, unlike atomic-electron term symbols, the lowest energy state is not L − S, but rather, l + s. All nuclear levels whose l value (orbital angular momentum) is greater than zero are thus split in the shell model to create states designated by l + s and l − s. Due to the nature of the shell modelShell model
In nuclear physics and nuclear chemistry, the nuclear shell model is a model of the atomic nucleus which uses the Pauli exclusion principle to describe the structure of the nucleus in terms of energy levels. The first shell model was proposed by Dmitry Ivanenko in 1932...
, which assumes an average potential rather than a central Coulombic potential, the nucleons that go into the l + s and l − s nuclear states are considered degenerate within each orbital (e.g. The 2p3/2 contains four nucleons, all of the same energy. Higher in energy is the 2p1/2 which contains two equal-energy nucleons).