Shell model
Encyclopedia
In nuclear physics
and nuclear chemistry
, the nuclear shell model is a model of the atomic nucleus
which uses the Pauli exclusion principle
to describe the structure of the nucleus in terms of energy levels. The first shell model was proposed by Dmitry Ivanenko (together with E. Gapon) in 1932. The model was developed in 1949 following independent work by several physicists, most notably Eugene Paul Wigner, Maria Goeppert-Mayer and J. Hans D. Jensen
, who shared the 1963 Nobel Prize in Physics
for their contributions.
The shell model is partly analogous to the atomic shell model
which describes the arrangement of electron
s in an atom, in that a filled shell results in greater stability. When adding nucleon
s (proton
s or neutron
s) to a nucleus, there are certain points where the binding energy of the next nucleon is significantly less than the last one. This observation, that there are certain magic number
s of nucleons: 2, 8, 20, 28, 50, 82, 126 which are more tightly bound than the next higher number, is the origin of the shell model.
Note that the shells exist for both protons and neutrons individually, so that we can speak of "magic nuclei" where one nucleon type is at a magic number, and "doubly magic nuclei", where both are. Due to some variations in orbital filling, the upper magic numbers are 126 and, speculatively, 184 for neutrons but only 114 for protons, playing a role in the search of the so-called island of stability
. There have been found some semimagic numbers, notably Z=40. 16 may also be a magic number.
In order to get these numbers, the nuclear shell model starts from an average potential with a shape something between the square well and the harmonic oscillator
. To this potential a spin orbit term is added. Even so, the total perturbation does not coincide with experiment, and an empirical spin orbit coupling, named the Nilsson Term, must be added with at least two or three different values of its coupling constant, depending on the nuclei being studied.
Nevertheless, the magic numbers of nucleons, as well as other properties, can be arrived at by approximating the model with a three-dimensional harmonic oscillator plus a spin-orbit interaction
. A more realistic but also complicated potential is known as Woods Saxon potential
.
Igal Talmi
developed a method to obtain the information from experimental data and use it to calculate and predict energies which have not been measured. This method has been successfully used by many nuclear physicists and has led to deeper understanding of nuclear structure. The theory which gives a good description of these properties was developed. This description turned out to furnish the shell model basis of the elegant and successful Interacting boson model
.
We can imagine ourselves building a nucleus by adding protons and neutrons. These will always fill the lowest available level. Thus the first two protons fill level zero, the next six protons fill level one, and so on. As with electrons in the periodic table
, protons in the outermost shell will be relatively loosely bound to the nucleus if there are only few protons in that shell, because they are farthest from the center of the nucleus. Therefore nuclei which have a full outer proton shell will have a higher binding energy
than other nuclei with a similar total number of protons. All this is true for neutrons as well.
This means that the magic numbers are expected to be those in which all occupied shells are full. We see that for the first two numbers we get 2 (level 0 full) and 8 (levels 0 and 1 full), in accord with experiment. However the full set of magic numbers does not turn out correctly. These can be computed as follows:
In particular, the first six shells are:
where for every l there are 2l+1 different values of ml and 2 values of ms, giving a total of 4l+2 states for every specific level.
These numbers are twice the values of triangular numbers from the Pascal Triangle: 1,3,6,10,15,21....
. First we have to describe the system by the quantum numbers j, mj and parity
instead of l, ml and ms, as in the Hydrogen-like atom. Since every even level includes only even values of l, it includes only states of even (positive) parity; Similarly every odd level includes only states of odd (negative) parity. Thus we can ignore parity in counting states. The first six shells, described by the new quantum numbers, are
where for every j there are different states from different values of mj.
Due to the spin-orbit interaction the energies of states of the same level but with different j will no longer be identical. This is because in the original quantum numbers, when
is parallel to 
, the interaction energy is negative; and in this case j = l + s = l + . When 
is anti-parallel to 
(i.e. aligned oppositely), the interaction energy is positive, and in this case . Furthermore, the strength of the interaction is roughly proportional to l.
For example, consider the states at level 4:
potential
grows infinitely as the distance from the center r goes to infinity. A more realistic potential, such as Woods Saxon potential
, would approach a constant at this limit. One main consequence is that the average radius of nucleons orbits would be larger in a realistic potential; This leads to a reduced term
in the Laplace operator
of the Hamiltonian
. Another main difference is that orbits with high average radii, such as those with high n or high l, will have a lower energy than in a harmonic oscillator potential. Both effects lead to a reduction in the energy levels of high l orbits.
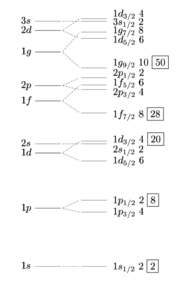Together with the spin-orbit interaction, and for appropriate magnitudes of both effects, one is led to the following qualitative picture: At all levels, the highest j states have their energies shifted downwards, especially for high n (where the highest j is high). This is both due to the negative spin-orbit interaction energy and to the reduction in energy resulting from deforming the potential to a more realistic one. The second-to-highest j states, on the contrary, have their energy shifted up by the first effect and down by the second effect, leading to a small overall shift. The shifts in the energy of the highest j states can thus bring the energy of states of one level to be closer to the energy of states of a lower level. The "shells" of the shell model are then no longer identical to the levels denoted by n, and the magic numbers are changed.
We may then suppose that the highest j states for n = 3 have an intermediate energy between the average energies of n = 2 and n = 3, and suppose that the highest j states for larger n (at least up to n = 7) have an energy closer to the average energy of . Then we get the following shells (see the figure)
and so on.
The magic numbers are then
and so on. This gives all the observed magic numbers, and also predicts a new one (the so-called island of stability
) at the value of 184 (for protons, the magic number 126 has not been observed yet, and more complicated theoretical considerations predict the magic number to be 114 instead).
Another way to predict magic (and semi-magic) numbers is by laying out the idealized filling order (with spin-orbit splitting but energy levels not overlapping). For consistency s is split into j = 1⁄2 and j = -1⁄2 components with 2 and 0 members respectively. Taking leftmost and rightmost total counts within sequences marked bounded by / here gives the magic and semi-magic numbers.
and parity
of nuclei ground state
s, and to some extent their excited state
s as well. Take as an example — its nucleus has eight protons filling the two first proton shells, eight neutrons filling the two first neutron shells, and one extra neutron. All protons in a complete proton shell have total angular momentum
zero, since their angular momenta cancel each other; The same is true for neutrons. All protons in the same level (n) have the same parity (either +1 or −1), and since the parity of a pair of particles is the product of their parities, an even number of protons from the same level (n) will have +1 parity. Thus the total angular momentum of the eight protons and the first eight neutrons is zero, and their total parity is +1. This means that the spin (i.e. angular momentum) of the nucleus, as well as its parity, are fully determined by that of the ninth neutron. This one is in the first (i.e. lowest energy) state of the 3rd shell, and therefore have n = 2, giving it +1 parity, and j = . Thus the nucleus of is expected to have positive parity and spin , which indeed it has.
For nuclei farther from the magic numbers
one must add the assumption that due to the relation between the strong nuclear force and angular momentum, proton
s or neutron
s with the same n tend to form pairs of opposite angular momenta. Therefore a nucleus with an even number of protons and an even number of neutrons has 0 spin and positive parity. A nucleus with an even number of protons and an odd number of neutrons (or vice versa) has the parity of the last neutron (or proton), and the spin equal to the total angular momentum of this neutron (or proton). By "last" we mean the properties coming from the highest energy level.
In the case of a nucleus with an odd number of protons and an odd number of neutrons, one must consider the total angular momentum and parity of both the last neutron and the last proton. The nucleus parity will be a product of theirs, while the nucleus spin will be one of the possible results of the sum of their angular momenta (with other possible results being excited states of the nucleus).
The ordering of angular momentum levels within each shell is according to the principles described above - due to spin-orbit interaction, with high angular momentum states having their energies shifted downwards due to the deformation of the potential (i.e. moving form a harmonic oscillator potential to a more realistic one). For nucleon pairs, however, it is often energetically favorable to be at high angular momentum, even if its energy level for a single nucleon would be higher. This is due to the relation between angular momentum and the strong nuclear force.
Nuclear magnetic moment
is partly predicted by this simple version of the shell model. The magnetic moment is calculated through j, l and s of the "last" nucleon, but nuclei are not in states of well defined l and s. Furthermore, for odd-odd nuclei, one has to consider the two "last" nucleons, as in deuterium. Therefore one gets several possible answers for the nuclear magnetic moment, one for each possible combined l and s state, and the real state of the nucleus is a superposition
of them. Thus the real (measured) nuclear magnetic moment is somewhere in between the possible answers.
The electric dipole of a nucleus is always zero, because its ground state
has a definite parity, so its matter density (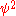
, where 
is the wavefunction
) is always invariant under parity. This is usually the situations with the atomic electric dipole as well.
Higher electric and magnetic multipole moments
cannot be predicted by this simple version of the shell model, for the reasons similar to those in the case of the deuterium.
Nuclear physics
Nuclear physics is the field of physics that studies the building blocks and interactions of atomic nuclei. The most commonly known applications of nuclear physics are nuclear power generation and nuclear weapons technology, but the research has provided application in many fields, including those...
and nuclear chemistry
Nuclear chemistry
Nuclear chemistry is the subfield of chemistry dealing with radioactivity, nuclear processes and nuclear properties.It is the chemistry of radioactive elements such as the actinides, radium and radon together with the chemistry associated with equipment which are designed to perform nuclear...
, the nuclear shell model is a model of the atomic nucleus
Atomic nucleus
The nucleus is the very dense region consisting of protons and neutrons at the center of an atom. It was discovered in 1911, as a result of Ernest Rutherford's interpretation of the famous 1909 Rutherford experiment performed by Hans Geiger and Ernest Marsden, under the direction of Rutherford. The...
which uses the Pauli exclusion principle
Pauli exclusion principle
The Pauli exclusion principle is the quantum mechanical principle that no two identical fermions may occupy the same quantum state simultaneously. A more rigorous statement is that the total wave function for two identical fermions is anti-symmetric with respect to exchange of the particles...
to describe the structure of the nucleus in terms of energy levels. The first shell model was proposed by Dmitry Ivanenko (together with E. Gapon) in 1932. The model was developed in 1949 following independent work by several physicists, most notably Eugene Paul Wigner, Maria Goeppert-Mayer and J. Hans D. Jensen
J. Hans D. Jensen
Johannes Hans Daniel Jensen was a German nuclear physicist. During World War II, he worked on the German nuclear energy project, known as the Uranium Club, in which he made contributions to the separation of uranium isotopes. After the war Jensen was a professor at the University of Heidelberg...
, who shared the 1963 Nobel Prize in Physics
Nobel Prize in Physics
The Nobel Prize in Physics is awarded once a year by the Royal Swedish Academy of Sciences. It is one of the five Nobel Prizes established by the will of Alfred Nobel in 1895 and awarded since 1901; the others are the Nobel Prize in Chemistry, Nobel Prize in Literature, Nobel Peace Prize, and...
for their contributions.
The shell model is partly analogous to the atomic shell model
Electron configuration
In atomic physics and quantum chemistry, electron configuration is the arrangement of electrons of an atom, a molecule, or other physical structure...
which describes the arrangement of electron
Electron
The electron is a subatomic particle with a negative elementary electric charge. It has no known components or substructure; in other words, it is generally thought to be an elementary particle. An electron has a mass that is approximately 1/1836 that of the proton...
s in an atom, in that a filled shell results in greater stability. When adding nucleon
Nucleon
In physics, a nucleon is a collective name for two particles: the neutron and the proton. These are the two constituents of the atomic nucleus. Until the 1960s, the nucleons were thought to be elementary particles...
s (proton
Proton
The proton is a subatomic particle with the symbol or and a positive electric charge of 1 elementary charge. One or more protons are present in the nucleus of each atom, along with neutrons. The number of protons in each atom is its atomic number....
s or neutron
Neutron
The neutron is a subatomic hadron particle which has the symbol or , no net electric charge and a mass slightly larger than that of a proton. With the exception of hydrogen, nuclei of atoms consist of protons and neutrons, which are therefore collectively referred to as nucleons. The number of...
s) to a nucleus, there are certain points where the binding energy of the next nucleon is significantly less than the last one. This observation, that there are certain magic number
Magic number (physics)
In nuclear physics, a magic number is a number of nucleons such that they are arranged into complete shells within the atomic nucleus...
s of nucleons: 2, 8, 20, 28, 50, 82, 126 which are more tightly bound than the next higher number, is the origin of the shell model.
Note that the shells exist for both protons and neutrons individually, so that we can speak of "magic nuclei" where one nucleon type is at a magic number, and "doubly magic nuclei", where both are. Due to some variations in orbital filling, the upper magic numbers are 126 and, speculatively, 184 for neutrons but only 114 for protons, playing a role in the search of the so-called island of stability
Island of stability
The island of stability in nuclear physics describes a set of as-yet undiscovered isotopes of transuranium elements which are theorized to be much more stable than others...
. There have been found some semimagic numbers, notably Z=40. 16 may also be a magic number.
In order to get these numbers, the nuclear shell model starts from an average potential with a shape something between the square well and the harmonic oscillator
Harmonic oscillator
In classical mechanics, a harmonic oscillator is a system that, when displaced from its equilibrium position, experiences a restoring force, F, proportional to the displacement, x: \vec F = -k \vec x \, where k is a positive constant....
. To this potential a spin orbit term is added. Even so, the total perturbation does not coincide with experiment, and an empirical spin orbit coupling, named the Nilsson Term, must be added with at least two or three different values of its coupling constant, depending on the nuclei being studied.
Nevertheless, the magic numbers of nucleons, as well as other properties, can be arrived at by approximating the model with a three-dimensional harmonic oscillator plus a spin-orbit interaction
Spin-orbit interaction
In quantum physics, the spin-orbit interaction is any interaction of a particle's spin with its motion. The first and best known example of this is that spin-orbit interaction causes shifts in an electron's atomic energy levels due to electromagnetic interaction between the electron's spin and...
. A more realistic but also complicated potential is known as Woods Saxon potential
Woods Saxon potential
The Woods–Saxon potential is a mean field potential for the nucleons inside the atomic nucleus, which is used to approximately describe the forces applied on each nucleon, in the shell model for the structure of the nucleus....
.
Igal Talmi
Igal Talmi
Igal Talmi is a distinguished Israeli nuclear physicist.-Biography:Igal Talmi was born in 1925 in Kiev, Ukraine, then part of the Soviet Union. His family immigrated to Mandate Palestine later that year and settled in Kfar Yehezkel...
developed a method to obtain the information from experimental data and use it to calculate and predict energies which have not been measured. This method has been successfully used by many nuclear physicists and has led to deeper understanding of nuclear structure. The theory which gives a good description of these properties was developed. This description turned out to furnish the shell model basis of the elegant and successful Interacting boson model
Interacting boson model
The interacting boson model is a model in nuclear physics in whichnucleons pair up, essentiallyacting as a single particle with boson properties, withintegral spin of 0, 2 or 4....
.
Deformed harmonic oscillator approximated model
Consider a three-dimensional harmonic oscillator. This would give, for example, in the first two levels ("l" is angular momentum)| level n | l | ml | ms |
|---|---|---|---|
| 0 | 0 | 0 | |
| − | |||
| 1 | 1 | 1 | |
| − | |||
| 0 | |||
| − | |||
| −1 | |||
| − |
We can imagine ourselves building a nucleus by adding protons and neutrons. These will always fill the lowest available level. Thus the first two protons fill level zero, the next six protons fill level one, and so on. As with electrons in the periodic table
Periodic table
The periodic table of the chemical elements is a tabular display of the 118 known chemical elements organized by selected properties of their atomic structures. Elements are presented by increasing atomic number, the number of protons in an atom's atomic nucleus...
, protons in the outermost shell will be relatively loosely bound to the nucleus if there are only few protons in that shell, because they are farthest from the center of the nucleus. Therefore nuclei which have a full outer proton shell will have a higher binding energy
Binding energy
Binding energy is the mechanical energy required to disassemble a whole into separate parts. A bound system typically has a lower potential energy than its constituent parts; this is what keeps the system together—often this means that energy is released upon the creation of a bound state...
than other nuclei with a similar total number of protons. All this is true for neutrons as well.
This means that the magic numbers are expected to be those in which all occupied shells are full. We see that for the first two numbers we get 2 (level 0 full) and 8 (levels 0 and 1 full), in accord with experiment. However the full set of magic numbers does not turn out correctly. These can be computed as follows:
- In a three-dimensional harmonic oscillator the total degeneracyDegenerate energy levelIn physics, two or more different quantum states are said to be degenerate if they are all at the same energy level. Statistically this means that they are all equally probable of being filled, and in Quantum Mechanics it is represented mathematically by the Hamiltonian for the system having more...
at level n is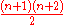
. Due to the spinSpin (physics)In quantum mechanics and particle physics, spin is a fundamental characteristic property of elementary particles, composite particles , and atomic nuclei.It is worth noting that the intrinsic property of subatomic particles called spin and discussed in this article, is related in some small ways,...
, the degeneracy is doubled and is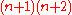
. - Thus the magic numbers would be
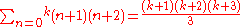
- for all integer k. This gives the following magic numbers: 2,8,20,40,70,112..., which agree with experiment only in the first three entries.
In particular, the first six shells are:
- level 0: 2 states (l = 0) = 2.
- level 1: 6 states (l = 1) = 6.
- level 2: 2 states (l = 0) + 10 states (l = 2) = 12.
- level 3: 6 states (l = 1) + 14 states (l = 3) = 20.
- level 4: 2 states (l = 0) + 10 states (l = 2) + 18 states (l = 4) = 30.
- level 5: 6 states (l = 1) + 14 states (l = 3) + 22 states (l = 5) = 42.
where for every l there are 2l+1 different values of ml and 2 values of ms, giving a total of 4l+2 states for every specific level.
These numbers are twice the values of triangular numbers from the Pascal Triangle: 1,3,6,10,15,21....
Including a spin-orbit interaction
We next include a spin-orbit interactionSpin-orbit interaction
In quantum physics, the spin-orbit interaction is any interaction of a particle's spin with its motion. The first and best known example of this is that spin-orbit interaction causes shifts in an electron's atomic energy levels due to electromagnetic interaction between the electron's spin and...
. First we have to describe the system by the quantum numbers j, mj and parity
Parity (physics)
In physics, a parity transformation is the flip in the sign of one spatial coordinate. In three dimensions, it is also commonly described by the simultaneous flip in the sign of all three spatial coordinates:...
instead of l, ml and ms, as in the Hydrogen-like atom. Since every even level includes only even values of l, it includes only states of even (positive) parity; Similarly every odd level includes only states of odd (negative) parity. Thus we can ignore parity in counting states. The first six shells, described by the new quantum numbers, are
- level 0 (n=0): 2 states (j = ). Even parity.
- level 1 (n=1): 2 states (j = ) + 4 states (j = ) = 6. Odd parity.
- level 2 (n=2): 2 states (j = ) + 4 states (j = ) + 6 states (j = ) = 12. Even parity.
- level 3 (n=3): 2 states (j = ) + 4 states (j = ) + 6 states (j = ) + 8 states (j = ) = 20. Odd parity.
- level 4 (n=4): 2 states (j = ) + 4 states (j = ) + 6 states (j = ) + 8 states (j = ) + 10 states (j = ) = 30. Even parity.
- level 5 (n=5): 2 states (j = ) + 4 states (j = ) + 6 states (j = ) + 8 states (j = ) + 10 states (j = ) + 12 states (j = ) = 42. Odd parity.
where for every j there are different states from different values of mj.
Due to the spin-orbit interaction the energies of states of the same level but with different j will no longer be identical. This is because in the original quantum numbers, when
is parallel to , the interaction energy is negative; and in this case j = l + s = l + . When is anti-parallel to (i.e. aligned oppositely), the interaction energy is positive, and in this case . Furthermore, the strength of the interaction is roughly proportional to l.For example, consider the states at level 4:
- The 10 states with j = come from l = 4 and s parallel to l. Thus they have a negative spin-orbit interaction energy.
- The 8 states with j = came from l = 4 and s anti-parallel to l. Thus they have a positive spin-orbit interaction energy.
- The 6 states with j = came from l = 2 and s parallel to l. Thus they have a negative spin-orbit interaction energy. However its magnitude is half compared to the states with j = .
- The 4 states with j = came from l = 2 and s anti-parallel to l. Thus they have a positive spin-orbit interaction energy. However its magnitude is half compared to the states with j = .
- The 2 states with j = came from l = 0 and thus have zero spin-orbit interaction energy.
Deforming the potential
The harmonic oscillatorHarmonic oscillator
In classical mechanics, a harmonic oscillator is a system that, when displaced from its equilibrium position, experiences a restoring force, F, proportional to the displacement, x: \vec F = -k \vec x \, where k is a positive constant....
potential
grows infinitely as the distance from the center r goes to infinity. A more realistic potential, such as Woods Saxon potentialWoods Saxon potential
The Woods–Saxon potential is a mean field potential for the nucleons inside the atomic nucleus, which is used to approximately describe the forces applied on each nucleon, in the shell model for the structure of the nucleus....
, would approach a constant at this limit. One main consequence is that the average radius of nucleons orbits would be larger in a realistic potential; This leads to a reduced term
in the Laplace operatorLaplace operator
In mathematics the Laplace operator or Laplacian is a differential operator given by the divergence of the gradient of a function on Euclidean space. It is usually denoted by the symbols ∇·∇, ∇2 or Δ...
of the Hamiltonian
Hamiltonian (quantum mechanics)
In quantum mechanics, the Hamiltonian H, also Ȟ or Ĥ, is the operator corresponding to the total energy of the system. Its spectrum is the set of possible outcomes when one measures the total energy of a system...
. Another main difference is that orbits with high average radii, such as those with high n or high l, will have a lower energy than in a harmonic oscillator potential. Both effects lead to a reduction in the energy levels of high l orbits.
Predicted magic numbers
We may then suppose that the highest j states for n = 3 have an intermediate energy between the average energies of n = 2 and n = 3, and suppose that the highest j states for larger n (at least up to n = 7) have an energy closer to the average energy of . Then we get the following shells (see the figure)
- 1st shell: 2 states (n = 0, j = ).
- 2nd shell: 6 states (n = 1, j = or ).
- 3rd shell: 12 states (n = 2, j = , or ).
- 4th shell: 8 states (n = 3, j = ).
- 5th shell: 22 states (n = 3, j = , or ; n = 4, j = ).
- 6th shell: 32 states (n = 4, j = , , or ; n = 5, j = ).
- 7th shell: 44 states (n = 5, j = , , , or ; n = 6, j = ).
- 8th shell: 58 states (n = 6, j = , , , , or ; n = 7, j = ).
and so on.
The magic numbers are then
- 2
- |2|+|6|+|12|+|8|+|22|+|32|+|44}}|2|+|6|+|12|+|8|+|22|+|32|+|44|+|58}}
and so on. This gives all the observed magic numbers, and also predicts a new one (the so-called island of stability
Island of stability
The island of stability in nuclear physics describes a set of as-yet undiscovered isotopes of transuranium elements which are theorized to be much more stable than others...
) at the value of 184 (for protons, the magic number 126 has not been observed yet, and more complicated theoretical considerations predict the magic number to be 114 instead).
Another way to predict magic (and semi-magic) numbers is by laying out the idealized filling order (with spin-orbit splitting but energy levels not overlapping). For consistency s is split into j = 1⁄2 and j = -1⁄2 components with 2 and 0 members respectively. Taking leftmost and rightmost total counts within sequences marked bounded by / here gives the magic and semi-magic numbers.
- s(2,0)/p(4,2)> 2,2/6,8, so (semi)magic numbers 2,2/6,8
- d(6,4):s(2,0)/f(8,6):p(4,2)> 14,18:20,20/28,34:38,40, so 14,20/28,40
- g(10,8):d(6,4):s(2,0)/h(12,10):f(8,6):p(4,2)> 50,58,64,68,70,70/82,92,100,106,110,112, so 50,70/82,112
- i(14,12):g(10,8):d(6,4):s(2,0)/j(16,14):h(12,10):f(8,6):p(4,2)> 126,138,148,156,162,166,168,168/184,198,210,220,228,234,238,240, so 126,168/184,240
Other properties of nuclei
This model also predicts or explains with some success other properties of nuclei, in particular spinSpin (physics)
In quantum mechanics and particle physics, spin is a fundamental characteristic property of elementary particles, composite particles , and atomic nuclei.It is worth noting that the intrinsic property of subatomic particles called spin and discussed in this article, is related in some small ways,...
and parity
Parity (physics)
In physics, a parity transformation is the flip in the sign of one spatial coordinate. In three dimensions, it is also commonly described by the simultaneous flip in the sign of all three spatial coordinates:...
of nuclei ground state
Ground state
The ground state of a quantum mechanical system is its lowest-energy state; the energy of the ground state is known as the zero-point energy of the system. An excited state is any state with energy greater than the ground state...
s, and to some extent their excited state
Excited state
Excitation is an elevation in energy level above an arbitrary baseline energy state. In physics there is a specific technical definition for energy level which is often associated with an atom being excited to an excited state....
s as well. Take as an example — its nucleus has eight protons filling the two first proton shells, eight neutrons filling the two first neutron shells, and one extra neutron. All protons in a complete proton shell have total angular momentum
Angular momentum
In physics, angular momentum, moment of momentum, or rotational momentum is a conserved vector quantity that can be used to describe the overall state of a physical system...
zero, since their angular momenta cancel each other; The same is true for neutrons. All protons in the same level (n) have the same parity (either +1 or −1), and since the parity of a pair of particles is the product of their parities, an even number of protons from the same level (n) will have +1 parity. Thus the total angular momentum of the eight protons and the first eight neutrons is zero, and their total parity is +1. This means that the spin (i.e. angular momentum) of the nucleus, as well as its parity, are fully determined by that of the ninth neutron. This one is in the first (i.e. lowest energy) state of the 3rd shell, and therefore have n = 2, giving it +1 parity, and j = . Thus the nucleus of is expected to have positive parity and spin , which indeed it has.
For nuclei farther from the magic numbers
Magic number (physics)
In nuclear physics, a magic number is a number of nucleons such that they are arranged into complete shells within the atomic nucleus...
one must add the assumption that due to the relation between the strong nuclear force and angular momentum, proton
Proton
The proton is a subatomic particle with the symbol or and a positive electric charge of 1 elementary charge. One or more protons are present in the nucleus of each atom, along with neutrons. The number of protons in each atom is its atomic number....
s or neutron
Neutron
The neutron is a subatomic hadron particle which has the symbol or , no net electric charge and a mass slightly larger than that of a proton. With the exception of hydrogen, nuclei of atoms consist of protons and neutrons, which are therefore collectively referred to as nucleons. The number of...
s with the same n tend to form pairs of opposite angular momenta. Therefore a nucleus with an even number of protons and an even number of neutrons has 0 spin and positive parity. A nucleus with an even number of protons and an odd number of neutrons (or vice versa) has the parity of the last neutron (or proton), and the spin equal to the total angular momentum of this neutron (or proton). By "last" we mean the properties coming from the highest energy level.
In the case of a nucleus with an odd number of protons and an odd number of neutrons, one must consider the total angular momentum and parity of both the last neutron and the last proton. The nucleus parity will be a product of theirs, while the nucleus spin will be one of the possible results of the sum of their angular momenta (with other possible results being excited states of the nucleus).
The ordering of angular momentum levels within each shell is according to the principles described above - due to spin-orbit interaction, with high angular momentum states having their energies shifted downwards due to the deformation of the potential (i.e. moving form a harmonic oscillator potential to a more realistic one). For nucleon pairs, however, it is often energetically favorable to be at high angular momentum, even if its energy level for a single nucleon would be higher. This is due to the relation between angular momentum and the strong nuclear force.
Nuclear magnetic moment
Nuclear magnetic moment
The nuclear magnetic moment is the magnetic moment of an atomic nucleus and arises from the spin of the protons and neutrons. It is mainly a magnetic dipole moment; the quadrupole moment does cause some small shifts in the hyperfine structure as well....
is partly predicted by this simple version of the shell model. The magnetic moment is calculated through j, l and s of the "last" nucleon, but nuclei are not in states of well defined l and s. Furthermore, for odd-odd nuclei, one has to consider the two "last" nucleons, as in deuterium. Therefore one gets several possible answers for the nuclear magnetic moment, one for each possible combined l and s state, and the real state of the nucleus is a superposition
Superposition principle
In physics and systems theory, the superposition principle , also known as superposition property, states that, for all linear systems, the net response at a given place and time caused by two or more stimuli is the sum of the responses which would have been caused by each stimulus individually...
of them. Thus the real (measured) nuclear magnetic moment is somewhere in between the possible answers.
The electric dipole of a nucleus is always zero, because its ground state
Ground state
The ground state of a quantum mechanical system is its lowest-energy state; the energy of the ground state is known as the zero-point energy of the system. An excited state is any state with energy greater than the ground state...
has a definite parity, so its matter density (
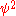, where is the wavefunctionWavefunction
Not to be confused with the related concept of the Wave equationA wave function or wavefunction is a probability amplitude in quantum mechanics describing the quantum state of a particle and how it behaves. Typically, its values are complex numbers and, for a single particle, it is a function of...
) is always invariant under parity. This is usually the situations with the atomic electric dipole as well.
Higher electric and magnetic multipole moments
Multipole moments
In mathematics, especially as applied to physics, multipole moments are the coefficients of a series expansion of a potential due to continuous or discrete sources . A multipole moment usually involves powers of the distance to the origin, as well as some angular dependence...
cannot be predicted by this simple version of the shell model, for the reasons similar to those in the case of the deuterium.
See also
- Interacting boson modelInteracting boson modelThe interacting boson model is a model in nuclear physics in whichnucleons pair up, essentiallyacting as a single particle with boson properties, withintegral spin of 0, 2 or 4....
- Liquid drop model
- Nuclear structureNuclear structureUnderstanding the structure of the atomic nucleus is one of the central challenges in nuclear physics. This article is written from a nuclear physics perspective; as such, it is suggested that a casual reader first read the main nuclear physics article....
- Isomeric shiftIsomeric shiftThe isomeric shift is the shift on atomic spectral lines and gamma spectral lines, which occurs as a consequence of replacement of one nuclear isomer by another. It is usually called isomeric shift on atomic spectral lines and Mössbauer isomeric shift respectively...