
Atomic spectral line
Encyclopedia

Physics
Physics is a natural science that involves the study of matter and its motion through spacetime, along with related concepts such as energy and force. More broadly, it is the general analysis of nature, conducted in order to understand how the universe behaves.Physics is one of the oldest academic...
, atomic spectral lines are of two types:
- An emission line is formed when an electron makes a transition from a particular discrete energy levelEnergy levelA quantum mechanical system or particle that is bound -- that is, confined spatially—can only take on certain discrete values of energy. This contrasts with classical particles, which can have any energy. These discrete values are called energy levels...
of an atom, to a lower energy state, emitting a photon of a particular energy and wavelength. A spectrum of many such photons will show an emission spike at the wavelength associated with these photons. - An absorption line is formed when an electron makes a transition from a lower to a higher discrete energy state, with a photon being absorbed in the process. These absorbed photons generally come from background continuum radiation and a spectrum will show a drop in the continuum radiation at the wavelength associated with the absorbed photons.
The two states must be bound state
Bound state
In physics, a bound state describes a system where a particle is subject to a potential such that the particle has a tendency to remain localised in one or more regions of space...
s in which the electron is bound to the atom, so the transition is sometimes referred to as a "bound–bound" transition, as opposed to a transition in which the electron is ejected out of the atom completely ("bound–free" transition) into a continuum
Continuous spectrum
The spectrum of a linear operator is commonly divided into three parts: point spectrum, continuous spectrum, and residual spectrum.If H is a topological vector space and A:H \to H is a linear map, the spectrum of A is the set of complex numbers \lambda such that A - \lambda I : H \to H is not...
state, leaving an ionized
Ionization
Ionization is the process of converting an atom or molecule into an ion by adding or removing charged particles such as electrons or other ions. This is often confused with dissociation. A substance may dissociate without necessarily producing ions. As an example, the molecules of table sugar...
atom, and generating continuum radiation.
A photon
Photon
In physics, a photon is an elementary particle, the quantum of the electromagnetic interaction and the basic unit of light and all other forms of electromagnetic radiation. It is also the force carrier for the electromagnetic force...
with an energy equal to the energy difference between the levels is released or absorbed in the process. The frequency
 at which the spectral line occurs is related to the photon energy
at which the spectral line occurs is related to the photon energy  by Planck's law
by Planck's law  where
where  is Planck's constant.
is Planck's constant.Emission and absorption coefficients
An atomic spectral line refers to emission and absorption events in a gas in which is the density of atoms in the upper energy state for the line, and
is the density of atoms in the upper energy state for the line, and  is the density of atoms in the lower energy state for the line.
is the density of atoms in the lower energy state for the line.The emission of atomic line radiation may be described by an emission coefficient
 with units of energy/time/volume/solid angle. ε dt dV dΩ is then the energy emitted by a volume element
with units of energy/time/volume/solid angle. ε dt dV dΩ is then the energy emitted by a volume element  in time
in time  into solid angle
into solid angle  . For atomic line radiation:
. For atomic line radiation:
where
 is the Einstein coefficient for spontaneous emission, which is fixed by the intrinsic properties of the relevant atom for the two relevant energy levels.
is the Einstein coefficient for spontaneous emission, which is fixed by the intrinsic properties of the relevant atom for the two relevant energy levels.The absorption of atomic line radiation may be described by an absorption coefficient
 with units of 1/length. The expression κ' dx gives the fraction of intensity absorbed for a light beam at frequency ν while traveling distance dx. The absorption coefficient is given by:
with units of 1/length. The expression κ' dx gives the fraction of intensity absorbed for a light beam at frequency ν while traveling distance dx. The absorption coefficient is given by:
where
 and
and  are the Einstein coefficients for photo absorption and induced emission respectively. Like the coefficient
are the Einstein coefficients for photo absorption and induced emission respectively. Like the coefficient  , these are also fixed by the intrinsic properties of the relevant atom for the two relevant energy levels. For thermodynamics and for the application of Kirchhoff's law, it is necessary that the total absorption be expressed as the algebraic sum of two components, described respectively by
, these are also fixed by the intrinsic properties of the relevant atom for the two relevant energy levels. For thermodynamics and for the application of Kirchhoff's law, it is necessary that the total absorption be expressed as the algebraic sum of two components, described respectively by  and
and  , which may be regarded as positive and negative absorption, respectively the photo absorption and what is commonly called stimulated or induced emission.
, which may be regarded as positive and negative absorption, respectively the photo absorption and what is commonly called stimulated or induced emission.The above equations have ignored the influence of the spectral line shape. To be accurate, the above equations need to be multiplied by the (normalized) spectral line shape, in which case the units will change to include a 1/Hz term.
The number densities
 and
and  and the Einstein coefficients provide sufficient information to determine the absorption and emission rates, without further need for information about the physical state of the gas or about the local radiation field. Thus the above absorption and emission coefficients work for any state of the gas, so for equilibrium states and even for laser conditions.
and the Einstein coefficients provide sufficient information to determine the absorption and emission rates, without further need for information about the physical state of the gas or about the local radiation field. Thus the above absorption and emission coefficients work for any state of the gas, so for equilibrium states and even for laser conditions.In contrast to the Einstein coefficients, the number densities, however, are not set simply by the intrinsic properties of the relevant atom.
Equilibrium conditions
The number densities and
and  are set by the physical state of the gas in which the spectral line occurs, including the local specific radiative intensity
are set by the physical state of the gas in which the spectral line occurs, including the local specific radiative intensitySpecific radiative intensity
Specific intensity is a fundamental quantity used in theoretical physics that fully describes the field of classical electromagnetic radiation of any kind, including thermal radiation and light. It is a description based on radiometry rather than Maxwellian electromagnetic fields or photon...
. When that state is either one of strict thermodynamic equilibrium
Thermodynamic equilibrium
In thermodynamics, a thermodynamic system is said to be in thermodynamic equilibrium when it is in thermal equilibrium, mechanical equilibrium, radiative equilibrium, and chemical equilibrium. The word equilibrium means a state of balance...
, or one of so-called 'local thermodynamic equilibrium', then the distribution of atomic states of excitation (which includes
 and
and  ) determines the rates of atomic emissions and absorptions to be such that Kirchhoff's law of equality of radiative absorptivity and emissivity
) determines the rates of atomic emissions and absorptions to be such that Kirchhoff's law of equality of radiative absorptivity and emissivityKirchhoff's law of thermal radiation
In thermodynamics, Kirchhoff's law of thermal radiation, or Kirchhoff's law for short, is a general statement equating emission and absorption in heated objects, proposed by Gustav Kirchhoff in 1859, following from general considerations of thermodynamic equilibrium and detailed balance.An object...
shall hold. In strict thermodynamic equilibrium, the radiation field is said to be black body
Black body
A black body is an idealized physical body that absorbs all incident electromagnetic radiation. Because of this perfect absorptivity at all wavelengths, a black body is also the best possible emitter of thermal radiation, which it radiates incandescently in a characteristic, continuous spectrum...
radiation, and is described by Planck's law. For local thermodynamic equilibrium, the radiation field does not have be a black body field, but the rate of interatomic collisions must vastly exceed the rates of absorption and emission of quanta of light, so that the interatomic collisions entirely dominate the distribution of states of atomic excitation.
In the cases of thermodynamic equilibrium
Thermodynamic equilibrium
In thermodynamics, a thermodynamic system is said to be in thermodynamic equilibrium when it is in thermal equilibrium, mechanical equilibrium, radiative equilibrium, and chemical equilibrium. The word equilibrium means a state of balance...
and of local thermodynamic equilibrium, the densities of the atoms, both excited and unexcited, may be calculated from the Maxwell–Boltzmann distribution, but for other cases, (e.g. laser
Laser
A laser is a device that emits light through a process of optical amplification based on the stimulated emission of photons. The term "laser" originated as an acronym for Light Amplification by Stimulated Emission of Radiation...
s) the calculation is more complicated.
The Einstein coefficients
In 1916, Albert EinsteinAlbert Einstein
Albert Einstein was a German-born theoretical physicist who developed the theory of general relativity, effecting a revolution in physics. For this achievement, Einstein is often regarded as the father of modern physics and one of the most prolific intellects in human history...
proposed that there are essentially three processes occurring in the formation of an atomic spectral line. The three processes are referred to as spontaneous emission, stimulated emission and absorption and with each is associated an Einstein coefficient which is a measure of the probability of that particular process occurring.
Spontaneous emission
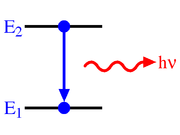
 will decay spontaneously to state 1 with energy
will decay spontaneously to state 1 with energy  , emitting a photon with an energy
, emitting a photon with an energy  . Due to the energy-time uncertainty principle, the transition actually produces photons within a narrow range of frequencies called the spectral linewidth
. Due to the energy-time uncertainty principle, the transition actually produces photons within a narrow range of frequencies called the spectral linewidthSpectral linewidth
The spectral linewidth characterizes the width of a spectral line, such as in the electromagnetic emission spectrum of an atom, or the frequency spectrum of an acoustic or electronic system...
. If
 is the number density of atoms in state i then the change in the number density of atoms in state 1 per unit time due to spontaneous emission will be:
is the number density of atoms in state i then the change in the number density of atoms in state 1 per unit time due to spontaneous emission will be:
Stimulated emission
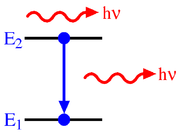
Stimulated emission
In optics, stimulated emission is the process by which an atomic electron interacting with an electromagnetic wave of a certain frequency may drop to a lower energy level, transferring its energy to that field. A photon created in this manner has the same phase, frequency, polarization, and...
(also known as induced emission) is the process by which an electron is induced to jump from a higher energy level to a lower one by the presence of electromagnetic radiation at (or near) the frequency of the transition. The process is described by the Einstein coefficient
 (sr·m2·Hz·W−1·s−1 = sr·m2·J−1·s−1), which gives the probability per unit time per unit spectral radiance of the radiation field that an electron in state 2 with energy
(sr·m2·Hz·W−1·s−1 = sr·m2·J−1·s−1), which gives the probability per unit time per unit spectral radiance of the radiation field that an electron in state 2 with energy  will decay to state 1 with energy
will decay to state 1 with energy  , emitting a photon with an energy
, emitting a photon with an energy  . The change in the number density of atoms in state 1 per unit time due to induced emission will be:
. The change in the number density of atoms in state 1 per unit time due to induced emission will be:
where
 is the radiation density of the radiation field at the frequency of the transition (see Planck's law).
is the radiation density of the radiation field at the frequency of the transition (see Planck's law).Stimulated emission is one of the fundamental processes that led to the development of the laser
Laser
A laser is a device that emits light through a process of optical amplification based on the stimulated emission of photons. The term "laser" originated as an acronym for Light Amplification by Stimulated Emission of Radiation...
.
Photo absorption
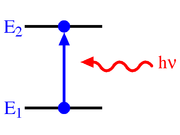
 (sr·m2·Hz·W−1·s−1 = sr·m2·J−1·s−1), which gives the probability per unit time per unit spectral radiance of the radiation field that an electron in state 1 with energy
(sr·m2·Hz·W−1·s−1 = sr·m2·J−1·s−1), which gives the probability per unit time per unit spectral radiance of the radiation field that an electron in state 1 with energy  will absorb a photon with an energy
will absorb a photon with an energy  and jump to state 2 with energy
and jump to state 2 with energy  . The change in the number density of atoms in state 1 per unit time due to absorption will be:
. The change in the number density of atoms in state 1 per unit time due to absorption will be:
Detailed balancing
The Einstein coefficients are fixed probabilities associated with each atom, and do not depend on the state of the gas of which the atoms are a part. Therefore, any relationship that we can derive between the coefficients at, say, thermal equilibrium will be valid universally.At equilibrium, we will have a simple balancing, in which the net change in the number of any excited atoms is zero, being balanced by loss and gain due to all processes. With respect to bound-bound transitions, we will have detailed balancing
Detailed balance
The principle of detailed balance is formulated for kinetic systems which are decomposed into elementary processes : At equilibrium, each elementary process should be equilibrated by its reverse process....
as well, which states that the net exchange between any two levels will be balanced. This is because the probabilities of transition cannot be affected by the presence or absence of other excited atoms. Detailed balance (valid only at equilibrium) requires that the change in time of the number of atoms in level 1 due to the above three processes be zero:

Along with detailed balancing, we may use our knowledge of the equilibrium energy distribution of the atoms, as stated in the Maxwell–Boltzmann distribution , and the equilibrium distribution of the photons, as stated in Planck's law of black body radiation
Planck's law of black body radiation
In physics, Planck's law describes the amount of energy emitted by a black body in radiation of a certain wavelength . The law is named after Max Planck, who originally proposed it in 1900. The law was the first to accurately describe black body radiation, and resolved the ultraviolet catastrophe...
to derive universal relationships between the Einstein coefficients.
From the Maxwell–Boltzmann distribution we have for the number of excited atomic specie i:

where n is the total density of the atomic specie, excited and unexcited, k is Boltzmann's constant, T is the temperature
Temperature
Temperature is a physical property of matter that quantitatively expresses the common notions of hot and cold. Objects of low temperature are cold, while various degrees of higher temperatures are referred to as warm or hot...
,
 is the degeneracy of state i, and Z is the partition function
is the degeneracy of state i, and Z is the partition functionPartition function (statistical mechanics)
Partition functions describe the statistical properties of a system in thermodynamic equilibrium. It is a function of temperature and other parameters, such as the volume enclosing a gas...
. From Planck's law of black body radiation we have for the spectral radiance at frequency


where:

where
 is the speed of light
is the speed of lightSpeed of light
The speed of light in vacuum, usually denoted by c, is a physical constant important in many areas of physics. Its value is 299,792,458 metres per second, a figure that is exact since the length of the metre is defined from this constant and the international standard for time...
and
 is Planck's constant.
is Planck's constant.Note that in some treatments, the blackbody energy density is used rather than the spectral radiance, in which case:

Substituting these expressions into the equation of detailed balancing and remembering that
 yields:
yields:
separating to:

The above equation must hold at any temperature, so


Therefore the three Einstein coefficients are interrelated by:

and

When this relation is inserted into the original equation, one can also find a relation between
 and
and  , involving Planck's law.
, involving Planck's law.Oscillator strengths
The oscillator strength is defined by the following relation to the cross section
is defined by the following relation to the cross section  for absorption:
for absorption:
where
 is the electron charge and
is the electron charge and  is the electron mass. This allows all three Einstein coefficients to be expressed in terms of the single oscillator strength associated with the particular atomic spectral line:
is the electron mass. This allows all three Einstein coefficients to be expressed in terms of the single oscillator strength associated with the particular atomic spectral line:


See also
- Transition dipole moment
- Oscillator strengthOscillator strengthAn atom or a molecule can absorb light and undergo a transition fromone quantum state to another. The oscillator strength is a dimensionlessquantity to express the strength of the transition....
- Breit–Wigner distribution
- Electronic configuration
- Fano resonanceFano resonanceIn physics, a Fano resonance is a type of resonant scattering phenomenon that gives rise to an asymmetric line-shape. Interference between a background and a resonant scattering process produces the asymmetric line-shape. It is named after Italian physicist Ugo Fano who gave a theoretical...
- Siegbahn notationSiegbahn notationThe Siegbahn notation is used in X-ray spectroscopy to name the spectral lines that are characteristic to elements. It was created by Manne Siegbahn....
- Atomic spectroscopyAtomic spectroscopyAtomic spectroscopy is the determination of elemental composition by its electromagnetic or mass spectrum. Atomic spectroscopy is closely related to other forms of spectroscopy. It can be divided by atomization source or by the type of spectroscopy used. In the latter case, the main division is...
- Molecular radiation, continuous spectra emitted by molecules

