
Specific radiative intensity
Encyclopedia
Specific intensity is a fundamental quantity used in theoretical physics that fully describes the field of classical electromagnetic
radiation
of any kind, including thermal radiation
and light
. It is a description based on radiometry rather than Maxwellian
electromagnetic fields or photon
distribution, and refers to material physics
as distinct from psychophysics
. Though it is not an SI term, specific (radiative) intensity can be expressed in SI units .
Specific intensity is a term used in much of the older scientific literature, but is nowadays not the preferred SI term for its purpose. Specific intensity is identical in meaning to the SI term spectral radiance. The theory of radiative transfer
uses the concept of specific intensity to give a radiometric description of a continuous field
of electromagnetic radiation. For this concept, the area of radiative emission is merely mathematical, lying in a semi-transparent medium which varies continuously in its optical properties.
The term brightness has also sometimes been used for this concept. The SI system states that the word brightness should not be so used, but should instead refer only to psychophysics.
where:
is defined to be such that a virtual source area, , containing the point , is an apparent emitter of a small but finite amount of energy transported by radiation of frequencies in a small time duration , where
and where is the angle between and the normal to ; the effective destination of is a finite small area , containing the point , that defines a finite small solid angle about in the direction of .
The use of the differential notation for areas indicates they are very small compared to , the square of the magnitude of vector , and thus the solid angles are also small.
There is no radiation that is attributed to itself as its source, because is a geometrical point
with no magnitude. A finite area is needed to emit a finite amount of light.
This may be understood by looking at the diagram. The factor has the effect of converting the effective emitting area into a virtual projected area at right angles to the vector from source to detector. The solid angle also has the effect of converting the detecting area into a virtual projected area at right angles to the vector , so that . Substituting this for in the above expression for the collected energy , one finds : when the emitting and detecting areas and angles and , and , are held constant, the collected energy is inversely proportional to the square of the distance between them, with invariant .
This may be expressed also by the statement that is invariant with respect to the length of ; that is to say, provided the optical devices have adequate resolution, and that the transmitting medium is perfectly transparent, as for example a vacuum, then the specific intensity of the source is unaffected by the length of the ray .
For the propagation of light in a transparent medium with a non-unit non-uniform refractive index, the invariant quantity along a ray is the specific intensity divided by the square of the absolute refractive index.
applies, because absorption and emission are the same for both senses of a given direction at a point in a stationary medium.
is used to focus attention specifically on the geometrical aspects. The reciprocal character of étendue
is indicated in the article about it. Étendue is defined as a second differential. In the notation of the present article, the second differential of the étendue, , of the pencil of light
which "connects" the two surface elements and is defined as
This can help understand the geometrical aspects of the Stokes-Helmholtz reversion-reciprocity principle.
, but apart from this, a collimated beam is rarely if ever found in nature, though artificially produced beams can be very nearly collimated. For some purposes the rays of the sun can be considered as practically collimated, because the sun subtends an angle of only 32′ of arc. The specific (radiative) intensity is suitable for the description of an uncollimated radiative field. The integrals of specific (radiative) intensity with respect to solid angle, used for the definition of spectral flux density
, are singular for exactly collimated beams, or may be viewed as Dirac delta function
s. Therefore the specific (radiative) intensity is unsuitable for the description of a collimated beam, while spectral flux density
is suitable for that purpose.
of rays of light
.
In an optically isotropic medium, the rays are normals to the wavefront
s, but in an optically anisotropic crystalline medium, they are in general at angles to those normals. That is to say, in an optically anisotropic crystal, the energy does not in general propagate at right angles to the wavefronts.
The idea common to the photon and the radiometric concepts is that the energy travels along rays.
Another way to describe the radiative field is in terms of the Maxwell electromagnetic field, which includes the concept of the wavefront
. The rays of the radiometric and photon concepts are along the time-averaged Poynting vector
of the Maxwell field. In an anisotropic medium, the rays are not in general perpendicular to the wavefront.
According to Paltridge and Platt (1976), there are various nomenclatures and general approaches to electromagnetic radiative transfer
. A term identical in meaning to the present term specific (radiative) intensity is spectral radiance
. These two terms are purely physically oriented without concern for the psychophysical aspect referred to by the term luminance
.
Classical electromagnetism
Classical electromagnetism is a branch of theoretical physics that studies consequences of the electromagnetic forces between electric charges and currents...
radiation
Electromagnetic radiation
Electromagnetic radiation is a form of energy that exhibits wave-like behavior as it travels through space...
of any kind, including thermal radiation
Thermal radiation
Thermal radiation is electromagnetic radiation generated by the thermal motion of charged particles in matter. All matter with a temperature greater than absolute zero emits thermal radiation....
and light
Light
Light or visible light is electromagnetic radiation that is visible to the human eye, and is responsible for the sense of sight. Visible light has wavelength in a range from about 380 nanometres to about 740 nm, with a frequency range of about 405 THz to 790 THz...
. It is a description based on radiometry rather than Maxwellian
James Clerk Maxwell
James Clerk Maxwell of Glenlair was a Scottish physicist and mathematician. His most prominent achievement was formulating classical electromagnetic theory. This united all previously unrelated observations, experiments and equations of electricity, magnetism and optics into a consistent theory...
electromagnetic fields or photon
Photon
In physics, a photon is an elementary particle, the quantum of the electromagnetic interaction and the basic unit of light and all other forms of electromagnetic radiation. It is also the force carrier for the electromagnetic force...
distribution, and refers to material physics
Physics
Physics is a natural science that involves the study of matter and its motion through spacetime, along with related concepts such as energy and force. More broadly, it is the general analysis of nature, conducted in order to understand how the universe behaves.Physics is one of the oldest academic...
as distinct from psychophysics
Psychophysics
Psychophysics quantitatively investigates the relationship between physical stimuli and the sensations and perceptions they effect. Psychophysics has been described as "the scientific study of the relation between stimulus and sensation" or, more completely, as "the analysis of perceptual...
. Though it is not an SI term, specific (radiative) intensity can be expressed in SI units .
Specific intensity is a term used in much of the older scientific literature, but is nowadays not the preferred SI term for its purpose. Specific intensity is identical in meaning to the SI term spectral radiance. The theory of radiative transfer
Radiative transfer
Radiative transfer is the physical phenomenon of energy transfer in the form of electromagnetic radiation. The propagation of radiation through a medium is affected by absorption, emission and scattering processes. The equation of radiative transfer describes these interactions mathematically...
uses the concept of specific intensity to give a radiometric description of a continuous field
Field (physics)
In physics, a field is a physical quantity associated with each point of spacetime. A field can be classified as a scalar field, a vector field, a spinor field, or a tensor field according to whether the value of the field at each point is a scalar, a vector, a spinor or, more generally, a tensor,...
of electromagnetic radiation. For this concept, the area of radiative emission is merely mathematical, lying in a semi-transparent medium which varies continuously in its optical properties.
The term brightness has also sometimes been used for this concept. The SI system states that the word brightness should not be so used, but should instead refer only to psychophysics.
Definition
The specific (radiative) intensity is a quantity that describes the rate of radiative transfer of energy at , a point of space with coordinates , at time . It is a scalar-valued function of four variables, customarily written aswhere:
- denotes frequency.
- denotes a unit vector, with the direction and sense of the geometrical vector from
- the point , to
- a detection point .
is defined to be such that a virtual source area, , containing the point , is an apparent emitter of a small but finite amount of energy transported by radiation of frequencies in a small time duration , where
- ,
and where is the angle between and the normal to ; the effective destination of is a finite small area , containing the point , that defines a finite small solid angle about in the direction of .
The use of the differential notation for areas indicates they are very small compared to , the square of the magnitude of vector , and thus the solid angles are also small.
There is no radiation that is attributed to itself as its source, because is a geometrical point
Point (geometry)
In geometry, topology and related branches of mathematics a spatial point is a primitive notion upon which other concepts may be defined. In geometry, points are zero-dimensional; i.e., they do not have volume, area, length, or any other higher-dimensional analogue. In branches of mathematics...
with no magnitude. A finite area is needed to emit a finite amount of light.
Invariance
For propagation of light in a vacuum, the definition of specific (radiative) intensity implicitly allows for the inverse square law of radiative propagation. The concept of specific (radiative) intensity of a source at the point presumes that the destination detector at the point has optical devices (telescopic lenses and so forth) that can resolve the details of the source area . Then the specific radiative intensity of the source is independent of the distance from source to detector; it is a property of the source alone. This is because it is defined per unit solid angle, the definition of which refers to the area of the detecting surface.This may be understood by looking at the diagram. The factor has the effect of converting the effective emitting area into a virtual projected area at right angles to the vector from source to detector. The solid angle also has the effect of converting the detecting area into a virtual projected area at right angles to the vector , so that . Substituting this for in the above expression for the collected energy , one finds : when the emitting and detecting areas and angles and , and , are held constant, the collected energy is inversely proportional to the square of the distance between them, with invariant .
This may be expressed also by the statement that is invariant with respect to the length of ; that is to say, provided the optical devices have adequate resolution, and that the transmitting medium is perfectly transparent, as for example a vacuum, then the specific intensity of the source is unaffected by the length of the ray .
For the propagation of light in a transparent medium with a non-unit non-uniform refractive index, the invariant quantity along a ray is the specific intensity divided by the square of the absolute refractive index.
Reciprocity
For the propagation of light in a semi-transparent medium, specific intensity is not invariant along a ray, because of absorption and emission. Nevertheless, the Stokes-Helmholtz reversion-reciprocity principleHelmholtz reciprocity
The Helmholtz reciprocity principle describes how a ray of light and its reverse ray encounter matched optical adventures, such as reflections, refractions, and absorptions in a passive medium, or at an interface....
applies, because absorption and emission are the same for both senses of a given direction at a point in a stationary medium.
Étendue and Reciprocity
The term étendueEtendue
Etendue or étendue is a property of pencils of rays in an optical system, which characterizes how "spread out" light is in area and angle. It may also be seen as a volume in phase space....
is used to focus attention specifically on the geometrical aspects. The reciprocal character of étendue
Etendue
Etendue or étendue is a property of pencils of rays in an optical system, which characterizes how "spread out" light is in area and angle. It may also be seen as a volume in phase space....
is indicated in the article about it. Étendue is defined as a second differential. In the notation of the present article, the second differential of the étendue, , of the pencil of light
Pencil beam
In optics, a pencil or pencil of rays is a geometric construct used to describe a beam or portion of a beam of electromagnetic radiation or charged particles, typically in the form of a narrow cone or cylinder....
which "connects" the two surface elements and is defined as
-
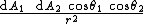 .
.
This can help understand the geometrical aspects of the Stokes-Helmholtz reversion-reciprocity principle.
Collimated beam
For the present purposes, the light from a star can be treated as a practically collimated beamCollimated light
Collimated light is light whose rays are parallel, and therefore will spread slowly as it propagates. The word is related to "collinear" and implies light that does not disperse with distance , or that will disperse minimally...
, but apart from this, a collimated beam is rarely if ever found in nature, though artificially produced beams can be very nearly collimated. For some purposes the rays of the sun can be considered as practically collimated, because the sun subtends an angle of only 32′ of arc. The specific (radiative) intensity is suitable for the description of an uncollimated radiative field. The integrals of specific (radiative) intensity with respect to solid angle, used for the definition of spectral flux density
Spectral flux density
In spectroscopy, spectral flux density is the quantity that describes the rate at which energy is transferred by electromagnetic radiation through a real or virtual surface, per unit surface area and per unit wavelength. It is a radiometric measure, as distinct from measures that characterize light...
, are singular for exactly collimated beams, or may be viewed as Dirac delta function
Dirac delta function
The Dirac delta function, or δ function, is a generalized function depending on a real parameter such that it is zero for all values of the parameter except when the parameter is zero, and its integral over the parameter from −∞ to ∞ is equal to one. It was introduced by theoretical...
s. Therefore the specific (radiative) intensity is unsuitable for the description of a collimated beam, while spectral flux density
Spectral flux density
In spectroscopy, spectral flux density is the quantity that describes the rate at which energy is transferred by electromagnetic radiation through a real or virtual surface, per unit surface area and per unit wavelength. It is a radiometric measure, as distinct from measures that characterize light...
is suitable for that purpose.
Rays
Specific (radiative) intensity is built on the idea of a pencilPencil beam
In optics, a pencil or pencil of rays is a geometric construct used to describe a beam or portion of a beam of electromagnetic radiation or charged particles, typically in the form of a narrow cone or cylinder....
of rays of light
Ray (optics)
In optics, a ray is an idealized narrow beam of light. Rays are used to model the propagation of light through an optical system, by dividing the real light field up into discrete rays that can be computationally propagated through the system by the techniques of ray tracing. This allows even very...
.
In an optically isotropic medium, the rays are normals to the wavefront
Wavefront
In physics, a wavefront is the locus of points having the same phase. Since infrared, optical, x-ray and gamma-ray frequencies are so high, the temporal component of electromagnetic waves is usually ignored at these wavelengths, and it is only the phase of the spatial oscillation that is described...
s, but in an optically anisotropic crystalline medium, they are in general at angles to those normals. That is to say, in an optically anisotropic crystal, the energy does not in general propagate at right angles to the wavefronts.
Alternative approaches
The specific (radiative) intensity is a radiometric concept. Related to it is the intensity in terms of the photon distribution function, which uses the metaphor of a particle of light that traces the path of a ray.The idea common to the photon and the radiometric concepts is that the energy travels along rays.
Another way to describe the radiative field is in terms of the Maxwell electromagnetic field, which includes the concept of the wavefront
Wavefront
In physics, a wavefront is the locus of points having the same phase. Since infrared, optical, x-ray and gamma-ray frequencies are so high, the temporal component of electromagnetic waves is usually ignored at these wavelengths, and it is only the phase of the spatial oscillation that is described...
. The rays of the radiometric and photon concepts are along the time-averaged Poynting vector
Poynting vector
In physics, the Poynting vector can be thought of as representing the directional energy flux density of an electromagnetic field. It is named after its inventor John Henry Poynting. Oliver Heaviside and Nikolay Umov independently co-invented the Poynting vector...
of the Maxwell field. In an anisotropic medium, the rays are not in general perpendicular to the wavefront.
According to Paltridge and Platt (1976), there are various nomenclatures and general approaches to electromagnetic radiative transfer
Radiative transfer
Radiative transfer is the physical phenomenon of energy transfer in the form of electromagnetic radiation. The propagation of radiation through a medium is affected by absorption, emission and scattering processes. The equation of radiative transfer describes these interactions mathematically...
. A term identical in meaning to the present term specific (radiative) intensity is spectral radiance
Radiance
Radiance and spectral radiance are radiometric measures that describe the amount of radiation such as light or radiant heat that passes through or is emitted from a particular area, and falls within a given solid angle in a specified direction. They are used to characterize both emission from...
. These two terms are purely physically oriented without concern for the psychophysical aspect referred to by the term luminance
Luminance
Luminance is a photometric measure of the luminous intensity per unit area of light travelling in a given direction. It describes the amount of light that passes through or is emitted from a particular area, and falls within a given solid angle. The SI unit for luminance is candela per square...
.

