Spectral flux density
Encyclopedia
In spectroscopy
, spectral flux density is the quantity that describes the rate at which energy
is transferred by electromagnetic radiation
through a real or virtual surface, per unit surface area and per unit wavelength. It is a radiometric
measure, as distinct from measures that characterize light in terms of the electromagnetic field
or photon
s. In SI units
it is measured in W m-3, though it is more practical to measure it in W m-2 nm-1 (1 W m-2 nm-1 = 1 GW m-3 = 1 W mm-3) or W m-2 μm-1 (1 W m-2 μm-1 = 1 MW m-3). The terms irradiance
, radiant exitance, radiant emittance, and radiosity
are closely related to spectral flux density.
The terms used to describe spectral flux density vary between fields, sometimes including adjectives such as "electromagnetic" or "radiative", and sometimes dropping the word "density". Applications include:
transferred by electromagnetic radiation
is received from that unresolved point source, per unit receiving area facing the source, per unit wavelength range. In SI units
it is measured in W m-3, though it is more practical to measure it in W m-2 nm-1 (1 W m-2 nm-1 = 1 GW m-3 = 1 W mm-3) or W m-2 μm-1 (1 W m-2 μm-1 = 1 MW m-3).
At any given wavelength λ, the spectral flux density, Fλ, can be determined by the following procedure:
Spectral flux density is often used as the quantity on the y-axis of a graph representing the spectrum
of a light-source, such as a star
.
or specific intensity) at the point, while the scalar definition refers to the many possible hemispheric integrals of the spectral radiance (or specific intensity) at the point. The vector definition seems to be preferred for theoretical investigations of the physics of the radiative field. The scalar definition seems to be preferred for practical applications.
where
denotes the spectral radiance (or specific intensity) at the point 
at time 
and frequency 
, 
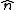denotes a variable unit vector with origin at the point 
, 
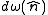denotes an element of solid angle arou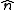nd 
, and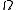 
indicates that the integration extends over the full range of solid angles of a sphere.
Mathematically, defined as an unweighted integral over the solid angle of a full sphere, the flux density is the first moment of the spectral radiance (or specific intensity) with respect to solid angle. It is not common practice to make the full spherical range of measurements of the spectral radiance (or specific intensity) at the point of interest, as is needed for the mathematical spherical integration specified in the strict definition; the concept is nevertheless used in theoretical analysis of radiative transfer.
As described below, if the direction of the flux density vector is known in advance because of a symmetry, namely that the radiative field is uniformly layered and flat, then the vector flux density can be measured as the 'net flux', by algebraic summation of two oppositely sensed pyrgeometric readings in the known direction, perpendicular to the layers.
At a given point in space, in a steady-state field, the vector flux density, a radiometric quantity, is equal to the time-averaged Poynting vector
, an electromagnetic field quantity.
Within the vector approach to the definition, however, there are several specialized sub-definitions. Sometimes the investigator is interested only in a specific direction, for example the vertical direction referred to a point in a planetary or stellar atmosphere, because the atmosphere there is considered to be the same in every horizontal direction, so that only the vertical component of the flux is of interest. Then the horizontal components of flux are considered to cancel each other by symmetry, leaving only the vertical component of the flux as non-zero. In this case some astrophysicists think in terms of the astrophysical flux (density), which they define as the vertical component of the flux (of the above general definition) divided by the number . And sometimes the astrophysicist uses the term Eddington flux to refer to the vertical component of the flux (of the above general definition) divided by the number .
where with the notation above,
indicates that the integration extends only over the solid angles of the relevant hemisphere, and 
denotes the angle between 
and the prescribed direction. The term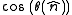 
is needed on account of Lambert's law
. Mathematically, the quantity
is not a vector because it is a positive scalar-valued function of the prescribed direction and sense, in this example, of the downward vertical. In this example, when the collected radiation is propagating in the downward sense, the detector is said to be "looking upwards". The measurement can be made directly with an instrument (such as a pyrgeometer) that collects the measured radiation all at once from all the directions of the imaginary hemisphere; in this case, Lambert-cosine-weighted integration of the spectral radiance (or specific intensity) is not performed mathematically after the measurement; the Lambert-cosine-weighted integration has been performed by the physical process of measurement itself.
and homogeneous
, let the spectral radiance (or specific intensity) be denoted by , a scalar-valued function of its arguments , , , and , where denotes a unit vector with the direction and sense of the geometrical vector from the source point to the detection point , where denotes the coordinates of , at time and wave frequency . Then, in the region, takes a constant scalar value, which we here denote by . In this case, the value of the vector flux density at is the zero vector, while the scalar or hemispheric flux density at in every direction in both senses takes the constant scalar value . The reason for the value is that the hemispheric integral is half the full spherical integral, and the integrated effect of the angles of incidence of the radiation on the detector requires a halving of the energy flux according to Lambert's cosine law
; the solid angle of a sphere is .
The vector definition is suitable for the study of general radiative fields. The scalar or hemispheric spectral flux density is convenient for discussions in terms of the two-stream model of the radiative field, which is reasonable for a field that is uniformly stratified in flat layers, when the base of the hemisphere is chosen to be parallel to the layers, and one or other sense (up or down) is specified. In an inhomogeneous non-isotropic radiative field, the spectral flux density defined as a scalar-valued function of direction and sense contains much more directional information than does the spectral flux density defined as a vector, but the full radiometric information is customarily stated as the spectral radiance (or specific intensity).
, but apart from this, a collimated beam is rarely if ever found in nature, though artificially produced beams can be very nearly collimated. The spectral radiance (or specific intensity) is suitable for the description of an uncollimated radiative field. The integrals of spectral radiance (or specific intensity) with respect to solid angle, used above, are singular for exactly collimated beams, or may be viewed as Dirac delta function
s. Therefore the specific radiative intenstity is unsuitable for the description of a collimated beam, while spectral flux density is suitable for that purpose. At a point within a collimated beam, the spectral flux density vector has a value equal to the Poynting vector
, a quantity defined in the classical Maxwell theory of electromagnetic radiation.
Spectra showing the relative spectral flux density are used when we are interested in comparing the spectral flux densities of different sources; for example, if we want to show how the spectra of blackbody sources vary with absolute temperature, it is not necessary to show the absolute values. The relative spectral flux density is also useful if we wish to compare a source's flux density at one wavelength with the same source's flux density at another wavelength; for example, if we wish to demonstrate how the Sun's spectrum peaks in the visible part of the EM spectrum, a graph of the Sun's relative spectral flux density will suffice.
Spectroscopy
Spectroscopy is the study of the interaction between matter and radiated energy. Historically, spectroscopy originated through the study of visible light dispersed according to its wavelength, e.g., by a prism. Later the concept was expanded greatly to comprise any interaction with radiative...
, spectral flux density is the quantity that describes the rate at which energy
Energy
In physics, energy is an indirectly observed quantity. It is often understood as the ability a physical system has to do work on other physical systems...
is transferred by electromagnetic radiation
Electromagnetic radiation
Electromagnetic radiation is a form of energy that exhibits wave-like behavior as it travels through space...
through a real or virtual surface, per unit surface area and per unit wavelength. It is a radiometric
Radiometry
In optics, radiometry is a set of techniques for measuring electromagnetic radiation, including visible light. Radiometric techniques characterize the distribution of the radiation's power in space, as opposed to photometric techniques, which characterize the light's interaction with the human eye...
measure, as distinct from measures that characterize light in terms of the electromagnetic field
Electromagnetic field
An electromagnetic field is a physical field produced by moving electrically charged objects. It affects the behavior of charged objects in the vicinity of the field. The electromagnetic field extends indefinitely throughout space and describes the electromagnetic interaction...
or photon
Photon
In physics, a photon is an elementary particle, the quantum of the electromagnetic interaction and the basic unit of light and all other forms of electromagnetic radiation. It is also the force carrier for the electromagnetic force...
s. In SI units
International System of Units
The International System of Units is the modern form of the metric system and is generally a system of units of measurement devised around seven base units and the convenience of the number ten. The older metric system included several groups of units...
it is measured in W m-3, though it is more practical to measure it in W m-2 nm-1 (1 W m-2 nm-1 = 1 GW m-3 = 1 W mm-3) or W m-2 μm-1 (1 W m-2 μm-1 = 1 MW m-3). The terms irradiance
Irradiance
Irradiance is the power of electromagnetic radiation per unit area incident on a surface. Radiant emittance or radiant exitance is the power per unit area radiated by a surface. The SI units for all of these quantities are watts per square meter , while the cgs units are ergs per square centimeter...
, radiant exitance, radiant emittance, and radiosity
Radiosity (heat transfer)
Radiosity is a convenient quantity in optics and heat transfer that represents the total radiation intensity leaving a surface. Radiosity accounts for two components: the radiation being emitted by the surface, and the radiation being reflected from the surface...
are closely related to spectral flux density.
The terms used to describe spectral flux density vary between fields, sometimes including adjectives such as "electromagnetic" or "radiative", and sometimes dropping the word "density". Applications include:
- Characterizing remote telescopically unresolved sources such as starStarA star is a massive, luminous sphere of plasma held together by gravity. At the end of its lifetime, a star can also contain a proportion of degenerate matter. The nearest star to Earth is the Sun, which is the source of most of the energy on Earth...
s, observed from a specified observation point such as an observatory on earth. - Characterizing a natural electromagnetic radiative field at a point, measured there with an instrument that collects radiation from a whole sphere or hemisphere of remote sources.
- Characterizing an artificial collimated electromagnetic radiative beam.
Flux density received from an unresolvable "point source"
For the flux density received from a remote unresolvable "point source", the measuring instrument, usually telescopic, though not able to resolve any detail of the source itself, must be able to optically resolve enough details of the sky around the point source, so as to record radiation coming from it only, uncontaminated by radiation from other sources. In this case, spectral flux density is the quantity that describes the rate at which energyEnergy
In physics, energy is an indirectly observed quantity. It is often understood as the ability a physical system has to do work on other physical systems...
transferred by electromagnetic radiation
Electromagnetic radiation
Electromagnetic radiation is a form of energy that exhibits wave-like behavior as it travels through space...
is received from that unresolved point source, per unit receiving area facing the source, per unit wavelength range. In SI units
International System of Units
The International System of Units is the modern form of the metric system and is generally a system of units of measurement devised around seven base units and the convenience of the number ten. The older metric system included several groups of units...
it is measured in W m-3, though it is more practical to measure it in W m-2 nm-1 (1 W m-2 nm-1 = 1 GW m-3 = 1 W mm-3) or W m-2 μm-1 (1 W m-2 μm-1 = 1 MW m-3).
At any given wavelength λ, the spectral flux density, Fλ, can be determined by the following procedure:
- An appropriate detector of cross-sectional area 1 m2 is pointed directly at the source of the radiation.
- A narrow band-pass filterBand-pass filterA band-pass filter is a device that passes frequencies within a certain range and rejects frequencies outside that range.Optical band-pass filters are of common usage....
is placed in front of the detector so that only radiation whose wavelength lies within a very narrow range, Δλ, centred on λ, reaches the detector.
- The rate at which EMElectromagnetic radiationElectromagnetic radiation is a form of energy that exhibits wave-like behavior as it travels through space...
energy is detected by the detector is measured.
- This measured rate is then divided by Δλ to obtain the detected power per square metre per unit wavelength range.
Spectral flux density is often used as the quantity on the y-axis of a graph representing the spectrum
Spectrum
A spectrum is a condition that is not limited to a specific set of values but can vary infinitely within a continuum. The word saw its first scientific use within the field of optics to describe the rainbow of colors in visible light when separated using a prism; it has since been applied by...
of a light-source, such as a star
Star
A star is a massive, luminous sphere of plasma held together by gravity. At the end of its lifetime, a star can also contain a proportion of degenerate matter. The nearest star to Earth is the Sun, which is the source of most of the energy on Earth...
.
Flux density of the radiative field at a measuring point
There are two main approaches to definition of the spectral flux density at a measuring point in an electromagnetic radiative field. One may be conveniently here labelled the 'vector approach', the other the 'scalar approach'. The vector definition refers to the full spherical integral of the spectral radiance (also known as the specific radiative intensitySpecific radiative intensity
Specific intensity is a fundamental quantity used in theoretical physics that fully describes the field of classical electromagnetic radiation of any kind, including thermal radiation and light. It is a description based on radiometry rather than Maxwellian electromagnetic fields or photon...
or specific intensity) at the point, while the scalar definition refers to the many possible hemispheric integrals of the spectral radiance (or specific intensity) at the point. The vector definition seems to be preferred for theoretical investigations of the physics of the radiative field. The scalar definition seems to be preferred for practical applications.
Vector definition of flux density - 'full spherical flux density'
The vector approach defines flux density as a vector at a point of space and time prescribed by the investigator. To distinguish this approach, one might speak of the 'full spherical flux density'. In this case, nature tells the investigator what is the magnitude, direction, and sense of the flux density at the prescribed point.. For the flux density vector, one may writewhere
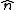denotes the spectral radiance (or specific intensity) at the point at time and frequency , denotes a variable unit vector with origin at the point , 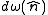denotes an element of solid angle around 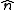, and indicates that the integration extends over the full range of solid angles of a sphere.Mathematically, defined as an unweighted integral over the solid angle of a full sphere, the flux density is the first moment of the spectral radiance (or specific intensity) with respect to solid angle. It is not common practice to make the full spherical range of measurements of the spectral radiance (or specific intensity) at the point of interest, as is needed for the mathematical spherical integration specified in the strict definition; the concept is nevertheless used in theoretical analysis of radiative transfer.
As described below, if the direction of the flux density vector is known in advance because of a symmetry, namely that the radiative field is uniformly layered and flat, then the vector flux density can be measured as the 'net flux', by algebraic summation of two oppositely sensed pyrgeometric readings in the known direction, perpendicular to the layers.
At a given point in space, in a steady-state field, the vector flux density, a radiometric quantity, is equal to the time-averaged Poynting vector
Poynting vector
In physics, the Poynting vector can be thought of as representing the directional energy flux density of an electromagnetic field. It is named after its inventor John Henry Poynting. Oliver Heaviside and Nikolay Umov independently co-invented the Poynting vector...
, an electromagnetic field quantity.
Within the vector approach to the definition, however, there are several specialized sub-definitions. Sometimes the investigator is interested only in a specific direction, for example the vertical direction referred to a point in a planetary or stellar atmosphere, because the atmosphere there is considered to be the same in every horizontal direction, so that only the vertical component of the flux is of interest. Then the horizontal components of flux are considered to cancel each other by symmetry, leaving only the vertical component of the flux as non-zero. In this case some astrophysicists think in terms of the astrophysical flux (density), which they define as the vertical component of the flux (of the above general definition) divided by the number . And sometimes the astrophysicist uses the term Eddington flux to refer to the vertical component of the flux (of the above general definition) divided by the number .
Scalar definition of flux density - 'hemispheric flux density'
The scalar approach defines flux density as a scalar-valued function of a direction and sense in space prescribed by the investigator at a point prescribed by the investigator. Sometimes this approach is indicated by the use of the term 'hemispheric flux'. For example, an investigator of thermal radiation, emitted from the material substance of the atmosphere, received at the surface of the earth, is interested in the vertical direction, and the downward sense in that direction. This investigator thinks of a unit area in a horizontal plane, surrounding the prescribed point. The investigator wants to know the total power of all the radiation from the atmosphere above in every direction, propagating with a downward sense, received by that unit area.. For the flux density scalar for the prescribed direction and sense, we may writewhere with the notation above,
indicates that the integration extends only over the solid angles of the relevant hemisphere, and denotes the angle between 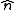and the prescribed direction. The term 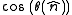is needed on account of Lambert's lawLambert's cosine law
In optics, Lambert's cosine law says that the radiant intensity observed from a Lambertian surface or a Lambertian radiator is directly proportional to the cosine of the angle θ between the observer's line of sight and the surface normal. A Lambertian surface is also known as an ideal diffusely...
. Mathematically, the quantity
is not a vector because it is a positive scalar-valued function of the prescribed direction and sense, in this example, of the downward vertical. In this example, when the collected radiation is propagating in the downward sense, the detector is said to be "looking upwards". The measurement can be made directly with an instrument (such as a pyrgeometer) that collects the measured radiation all at once from all the directions of the imaginary hemisphere; in this case, Lambert-cosine-weighted integration of the spectral radiance (or specific intensity) is not performed mathematically after the measurement; the Lambert-cosine-weighted integration has been performed by the physical process of measurement itself.Net flux
In a flat horizontal uniformly layered radiative field, the hemispheric fluxes, upwards and downwards, at a point, can be subtracted to yield what is often called the net flux. The net flux then has a value equal to the magnitude of the full spherical flux vector at that point, as described above.Comparison between vector and scalar definitions of flux density
The radiometric description of the electromagnetic radiative field at a point in space and time is completely represented by the spectral radiance (or specific intensity) at that point. In a region in which the material is uniform and the radiative field is isotropicIsotropy
Isotropy is uniformity in all orientations; it is derived from the Greek iso and tropos . Precise definitions depend on the subject area. Exceptions, or inequalities, are frequently indicated by the prefix an, hence anisotropy. Anisotropy is also used to describe situations where properties vary...
and homogeneous
Homogeneity (physics)
In general, homogeneity is defined as the quality or state of being homogeneous . For instance, a uniform electric field would be compatible with homogeneity...
, let the spectral radiance (or specific intensity) be denoted by , a scalar-valued function of its arguments , , , and , where denotes a unit vector with the direction and sense of the geometrical vector from the source point to the detection point , where denotes the coordinates of , at time and wave frequency . Then, in the region, takes a constant scalar value, which we here denote by . In this case, the value of the vector flux density at is the zero vector, while the scalar or hemispheric flux density at in every direction in both senses takes the constant scalar value . The reason for the value is that the hemispheric integral is half the full spherical integral, and the integrated effect of the angles of incidence of the radiation on the detector requires a halving of the energy flux according to Lambert's cosine law
Lambert's cosine law
In optics, Lambert's cosine law says that the radiant intensity observed from a Lambertian surface or a Lambertian radiator is directly proportional to the cosine of the angle θ between the observer's line of sight and the surface normal. A Lambertian surface is also known as an ideal diffusely...
; the solid angle of a sphere is .
The vector definition is suitable for the study of general radiative fields. The scalar or hemispheric spectral flux density is convenient for discussions in terms of the two-stream model of the radiative field, which is reasonable for a field that is uniformly stratified in flat layers, when the base of the hemisphere is chosen to be parallel to the layers, and one or other sense (up or down) is specified. In an inhomogeneous non-isotropic radiative field, the spectral flux density defined as a scalar-valued function of direction and sense contains much more directional information than does the spectral flux density defined as a vector, but the full radiometric information is customarily stated as the spectral radiance (or specific intensity).
Collimated beam
For the present purposes, the light from a star, and for some particular purposes, the light of the sun, can be treated as a practically collimated beamCollimated light
Collimated light is light whose rays are parallel, and therefore will spread slowly as it propagates. The word is related to "collinear" and implies light that does not disperse with distance , or that will disperse minimally...
, but apart from this, a collimated beam is rarely if ever found in nature, though artificially produced beams can be very nearly collimated. The spectral radiance (or specific intensity) is suitable for the description of an uncollimated radiative field. The integrals of spectral radiance (or specific intensity) with respect to solid angle, used above, are singular for exactly collimated beams, or may be viewed as Dirac delta function
Dirac delta function
The Dirac delta function, or δ function, is a generalized function depending on a real parameter such that it is zero for all values of the parameter except when the parameter is zero, and its integral over the parameter from −∞ to ∞ is equal to one. It was introduced by theoretical...
s. Therefore the specific radiative intenstity is unsuitable for the description of a collimated beam, while spectral flux density is suitable for that purpose. At a point within a collimated beam, the spectral flux density vector has a value equal to the Poynting vector
Poynting vector
In physics, the Poynting vector can be thought of as representing the directional energy flux density of an electromagnetic field. It is named after its inventor John Henry Poynting. Oliver Heaviside and Nikolay Umov independently co-invented the Poynting vector...
, a quantity defined in the classical Maxwell theory of electromagnetic radiation.
Relative spectral flux density
Sometimes it is more convenient to display graphical spectra with vertical axes that show the relative spectral flux density. In this case, the spectral flux density at a given wavelength is expressed as a fraction of some arbitrarily chosen reference value. Relative spectral flux densities are expressed as pure numbers without any units.Spectra showing the relative spectral flux density are used when we are interested in comparing the spectral flux densities of different sources; for example, if we want to show how the spectra of blackbody sources vary with absolute temperature, it is not necessary to show the absolute values. The relative spectral flux density is also useful if we wish to compare a source's flux density at one wavelength with the same source's flux density at another wavelength; for example, if we wish to demonstrate how the Sun's spectrum peaks in the visible part of the EM spectrum, a graph of the Sun's relative spectral flux density will suffice.