Poynting vector
Encyclopedia
In physics
, the Poynting vector can be thought of as representing the directional energy flux
density (the rate of energy transfer per unit area, in W/m2) of an electromagnetic field
. It is named after its inventor John Henry Poynting
. Oliver Heaviside
and Nikolay Umov
independently co-invented the Poynting vector. In Poynting's original paper and in many textbooks it is defined as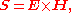
which is often called the Abraham form;
here E is the electric field
and H the auxiliary magnetic field. (All bold letters represent vectors.) Sometimes, an alternative definition in terms of electric field E and the magnetic field
B is used, which is explained below. It is even possible to combine the displacement field D with the magnetic field B to get the Minkowski form of the Poynting vector, or use D and H to construct another.
The choice has been controversial: Pfeifer et al.
summarize the century-long dispute between proponents of the Abraham and Minkowski forms.
, an energy-conservation law,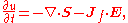
where Jf is the current density
of free charges and u is the electromagnetic energy density,
where B is the magnetic field
and D the electric displacement field.
The first term in the right-hand side represents the net electromagnetic energy flow into a small volume, while the second term represents the subtracted portion of the work done by free electrical currents that are not necessarily converted into electromagnetic energy (dissipation
, heat). In this definition, bound electrical currents are not included in this term, and instead contribute to S and u.
Note that u can only be given if linear, nondispersive
and uniform materials are involved, i.e., if the constitutive relations can be written as
where ε and μ are constants (which depend on the material through which the energy flows), called the permittivity
and permeability
, respectively, of the material.
This practically limits Poynting's theorem in this form to fields in vacuum. A generalization to dispersive materials is possible under certain circumstances at the cost of additional terms and the loss of their clear physical interpretation.
The Poynting vector is usually interpreted as an energy flux, but this is only strictly correct for electromagnetic radiation
. The more general case is described by Poynting's theorem above, where it occurs as a divergence
, which means that it can only describe the change of energy density in space, rather than the flow.
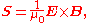
where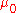
is the magnetic constant.
It can be derived directly from Maxwell's equations in terms of total charge and current and the Lorentz force
law only.
The corresponding form of Poynting's theorem
is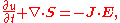
where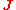
is the total current density
and the energy density
is
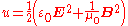
(with the electric constant
).
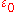The two alternative definitions of the Poynting vector are equivalent in vacuum or in non-magnetic materials, where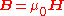
. In all other cases, they differ in that 
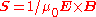and the corresponding u are purely radiative, since the dissipation term, 
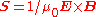, covers the total current, while the definition in terms of 
has contributions from bound currents which then lack in the dissipation term.
Since only the microscopic fields E and B are needed in the derivation of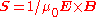
, assumptions about any material possibly present can be completely avoided, and Poynting's vector as well as the theorem in this definition are universally valid, in vacuum as in all kinds of material. This is especially true for the electromagnetic energy density, in contrast to the case above.
, the Poynting vector is arbitrary to the extent that one can add a field curl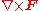 
, since 
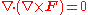for an arbitrary field F. Doing so is not common, though, and will lead to inconsistencies in a relativistic
description of electromagnetic
fields in terms of the stress-energy tensor
.
in 1874 describes energy flux in liquid and elastic media in a completely generalized view.
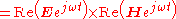
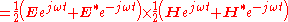
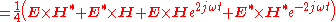
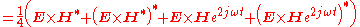
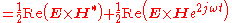
The average over time is given as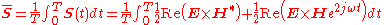
The second term is a sinusoidal curve (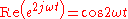
) whose average will be zero, which gives
.
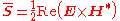insulator of a coaxial cable
is nearly parallel to the wire axis (assuming no fields outside the cable and a wavelength longer than the diameter of the cable, including DC). Electrical energy is flowing entirely through the dielectric between the conductor
s. No energy flows in the conductors themselves, since the electric field strength is zero. No energy flows outside the cable, either, since there the magnetic fields of inner and outer conductors cancel to zero.
and the very slow speed of light inside a conductor. See Hayt page 402 for the definition and computation of the speed of light in a conductor. Inside the conductor, the Poynting vector represents energy flow from the electromagnetic field
into the wire, producing resistive Joule heating
in the wire. For a derivation that starts with Snell's law see Reitz page 454.
of a fixed frequency, the Poynting vector always points in the direction of propagation while oscillating in magnitude. The time-averaged magnitude of the Poynting vector is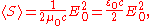
where
is the maximum amplitude of the electric field and 
is the speed of light
in free space. This time-averaged value is also called the irradiance
or intensity I.
and 
are always perpendicular to each other and the direction of propagation. Moreover, their amplitudes are related according to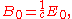
and their time and position dependences are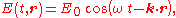
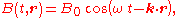
where
is the frequency of the wave and 
is wave vector
.
The time-dependent and position magnitude of the Poynting vector is then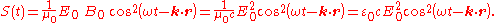
In the last step, we used the equality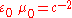
. Since the time- or space-average of 
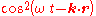is 
, it follows that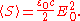
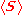divided by the speed of light in free space is the radiation pressure
exerted by an electromagnetic wave on the surface of a target:
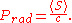
Physics
Physics is a natural science that involves the study of matter and its motion through spacetime, along with related concepts such as energy and force. More broadly, it is the general analysis of nature, conducted in order to understand how the universe behaves.Physics is one of the oldest academic...
, the Poynting vector can be thought of as representing the directional energy flux
Energy flux
Energy flux is the rate of transfer of energy through a surface. The quantity is defined in two different ways, depending on the context:# Rate of energy transfer per unit area...
density (the rate of energy transfer per unit area, in W/m2) of an electromagnetic field
Electromagnetic field
An electromagnetic field is a physical field produced by moving electrically charged objects. It affects the behavior of charged objects in the vicinity of the field. The electromagnetic field extends indefinitely throughout space and describes the electromagnetic interaction...
. It is named after its inventor John Henry Poynting
John Henry Poynting
John Henry Poynting was an English physicist. He was a professor of physics at Mason Science College from 1880 until his death....
. Oliver Heaviside
Oliver Heaviside
Oliver Heaviside was a self-taught English electrical engineer, mathematician, and physicist who adapted complex numbers to the study of electrical circuits, invented mathematical techniques to the solution of differential equations , reformulated Maxwell's field equations in terms of electric and...
and Nikolay Umov
Nikolay Umov
Nikolay Alekseevich Umov was a Russian physicist and mathematician known for discovering the concept of Umov-Poynting vector and Umov effect.-Biography:...
independently co-invented the Poynting vector. In Poynting's original paper and in many textbooks it is defined as
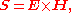
which is often called the Abraham form;
here E is the electric field
Electric field
In physics, an electric field surrounds electrically charged particles and time-varying magnetic fields. The electric field depicts the force exerted on other electrically charged objects by the electrically charged particle the field is surrounding...
and H the auxiliary magnetic field. (All bold letters represent vectors.) Sometimes, an alternative definition in terms of electric field E and the magnetic field
Magnetic field
A magnetic field is a mathematical description of the magnetic influence of electric currents and magnetic materials. The magnetic field at any given point is specified by both a direction and a magnitude ; as such it is a vector field.Technically, a magnetic field is a pseudo vector;...
B is used, which is explained below. It is even possible to combine the displacement field D with the magnetic field B to get the Minkowski form of the Poynting vector, or use D and H to construct another.
The choice has been controversial: Pfeifer et al.
summarize the century-long dispute between proponents of the Abraham and Minkowski forms.
Interpretation
The Poynting vector appears in Poynting's theoremPoynting's theorem
Poynting's theorem is a statement due to British physicist John Henry Poynting about the conservation of energy for the electromagnetic field. Poynting's theorem takes into account the case when the electric and magnetic fields are coupled – static or stationary electric and magnetic fields are not...
, an energy-conservation law,
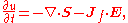
where Jf is the current density
Current density
Current density is a measure of the density of flow of a conserved charge. Usually the charge is the electric charge, in which case the associated current density is the electric current per unit area of cross section, but the term current density can also be applied to other conserved...
of free charges and u is the electromagnetic energy density,
where B is the magnetic field
Magnetic field
A magnetic field is a mathematical description of the magnetic influence of electric currents and magnetic materials. The magnetic field at any given point is specified by both a direction and a magnitude ; as such it is a vector field.Technically, a magnetic field is a pseudo vector;...
and D the electric displacement field.
The first term in the right-hand side represents the net electromagnetic energy flow into a small volume, while the second term represents the subtracted portion of the work done by free electrical currents that are not necessarily converted into electromagnetic energy (dissipation
Dissipation
In physics, dissipation embodies the concept of a dynamical system where important mechanical models, such as waves or oscillations, lose energy over time, typically from friction or turbulence. The lost energy converts into heat, which raises the temperature of the system. Such systems are called...
, heat). In this definition, bound electrical currents are not included in this term, and instead contribute to S and u.
Note that u can only be given if linear, nondispersive
Dispersion (optics)
In optics, dispersion is the phenomenon in which the phase velocity of a wave depends on its frequency, or alternatively when the group velocity depends on the frequency.Media having such a property are termed dispersive media...
and uniform materials are involved, i.e., if the constitutive relations can be written as
where ε and μ are constants (which depend on the material through which the energy flows), called the permittivity
Permittivity
In electromagnetism, absolute permittivity is the measure of the resistance that is encountered when forming an electric field in a medium. In other words, permittivity is a measure of how an electric field affects, and is affected by, a dielectric medium. The permittivity of a medium describes how...
and permeability
Permeability (electromagnetism)
In electromagnetism, permeability is the measure of the ability of a material to support the formation of a magnetic field within itself. In other words, it is the degree of magnetization that a material obtains in response to an applied magnetic field. Magnetic permeability is typically...
, respectively, of the material.
This practically limits Poynting's theorem in this form to fields in vacuum. A generalization to dispersive materials is possible under certain circumstances at the cost of additional terms and the loss of their clear physical interpretation.
The Poynting vector is usually interpreted as an energy flux, but this is only strictly correct for electromagnetic radiation
Electromagnetic radiation
Electromagnetic radiation is a form of energy that exhibits wave-like behavior as it travels through space...
. The more general case is described by Poynting's theorem above, where it occurs as a divergence
Divergence
In vector calculus, divergence is a vector operator that measures the magnitude of a vector field's source or sink at a given point, in terms of a signed scalar. More technically, the divergence represents the volume density of the outward flux of a vector field from an infinitesimal volume around...
, which means that it can only describe the change of energy density in space, rather than the flow.
Formulation in terms of microscopic fields
In some cases, it may be more appropriate to define the Poynting vector S as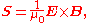where
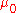is the magnetic constant.It can be derived directly from Maxwell's equations in terms of total charge and current and the Lorentz force
Lorentz force
In physics, the Lorentz force is the force on a point charge due to electromagnetic fields. It is given by the following equation in terms of the electric and magnetic fields:...
law only.
The corresponding form of Poynting's theorem
Poynting's theorem
Poynting's theorem is a statement due to British physicist John Henry Poynting about the conservation of energy for the electromagnetic field. Poynting's theorem takes into account the case when the electric and magnetic fields are coupled – static or stationary electric and magnetic fields are not...
is
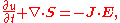
where
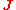is the total current densityCurrent density
Current density is a measure of the density of flow of a conserved charge. Usually the charge is the electric charge, in which case the associated current density is the electric current per unit area of cross section, but the term current density can also be applied to other conserved...
and the energy density
is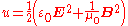(with the electric constant
Electric constant
The physical constant ε0, commonly called the vacuum permittivity, permittivity of free space or electric constant is an ideal, physical constant, which is the value of the absolute dielectric permittivity of classical vacuum...
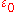).The two alternative definitions of the Poynting vector are equivalent in vacuum or in non-magnetic materials, where
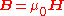. In all other cases, they differ in that 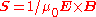and the corresponding u are purely radiative, since the dissipation term, 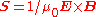, covers the total current, while the definition in terms of has contributions from bound currents which then lack in the dissipation term.Since only the microscopic fields E and B are needed in the derivation of
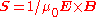, assumptions about any material possibly present can be completely avoided, and Poynting's vector as well as the theorem in this definition are universally valid, in vacuum as in all kinds of material. This is especially true for the electromagnetic energy density, in contrast to the case above.Invariance to adding a curl of a field
Since the Poynting vector only occurs in Poynting's theorem as a divergenceDivergence
In vector calculus, divergence is a vector operator that measures the magnitude of a vector field's source or sink at a given point, in terms of a signed scalar. More technically, the divergence represents the volume density of the outward flux of a vector field from an infinitesimal volume around...
, the Poynting vector is arbitrary to the extent that one can add a field curl 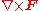, since 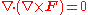for an arbitrary field F. Doing so is not common, though, and will lead to inconsistencies in a relativisticTheory of relativity
The theory of relativity, or simply relativity, encompasses two theories of Albert Einstein: special relativity and general relativity. However, the word relativity is sometimes used in reference to Galilean invariance....
description of electromagnetic
fields in terms of the stress-energy tensor
Stress-energy tensor
The stress–energy tensor is a tensor quantity in physics that describes the density and flux of energy and momentum in spacetime, generalizing the stress tensor of Newtonian physics. It is an attribute of matter, radiation, and non-gravitational force fields...
.
Generalization
The Poynting vector represents the particular case of an energy flux vector for electromagnetic energy. However, any type of energy has its direction of movement in space, as well as its density, so energy flux vectors can be defined for other types of energy as well, e.g., for mechanical energy. The Umov-Poynting vector discovered by Nikolay UmovNikolay Umov
Nikolay Alekseevich Umov was a Russian physicist and mathematician known for discovering the concept of Umov-Poynting vector and Umov effect.-Biography:...
in 1874 describes energy flux in liquid and elastic media in a completely generalized view.
Time-averaged Poynting vector
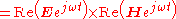
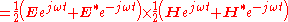
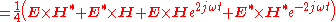
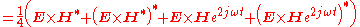
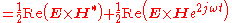
For time-harmonic (sinusoidal) electromagnetic fields, the average power flow over time is often more useful, and can be found as follows,The average over time is given as
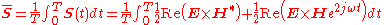
The second term is a sinusoidal curve (
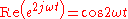) whose average will be zero, which gives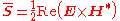.In a coaxial cable
For example, the Poynting vector within the dielectricDielectric
A dielectric is an electrical insulator that can be polarized by an applied electric field. When a dielectric is placed in an electric field, electric charges do not flow through the material, as in a conductor, but only slightly shift from their average equilibrium positions causing dielectric...
insulator of a coaxial cable
Coaxial cable
Coaxial cable, or coax, has an inner conductor surrounded by a flexible, tubular insulating layer, surrounded by a tubular conducting shield. The term coaxial comes from the inner conductor and the outer shield sharing the same geometric axis...
is nearly parallel to the wire axis (assuming no fields outside the cable and a wavelength longer than the diameter of the cable, including DC). Electrical energy is flowing entirely through the dielectric between the conductor
Electrical conductor
In physics and electrical engineering, a conductor is a material which contains movable electric charges. In metallic conductors such as copper or aluminum, the movable charged particles are electrons...
s. No energy flows in the conductors themselves, since the electric field strength is zero. No energy flows outside the cable, either, since there the magnetic fields of inner and outer conductors cancel to zero.
Resistive dissipation
If a conductor has significant resistance, then, near the surface of that conductor, the Poynting vector would be tilted toward and impinge upon the conductor. Once the Poynting vector enters the conductor, it is bent to a direction that is almost perpendicular to the surface. This is a consequence of Snell's lawSnell's law
In optics and physics, Snell's law is a formula used to describe the relationship between the angles of incidence and refraction, when referring to light or other waves passing through a boundary between two different isotropic media, such as water and glass...
and the very slow speed of light inside a conductor. See Hayt page 402 for the definition and computation of the speed of light in a conductor. Inside the conductor, the Poynting vector represents energy flow from the electromagnetic field
Electromagnetic field
An electromagnetic field is a physical field produced by moving electrically charged objects. It affects the behavior of charged objects in the vicinity of the field. The electromagnetic field extends indefinitely throughout space and describes the electromagnetic interaction...
into the wire, producing resistive Joule heating
Joule heating
Joule heating, also known as ohmic heating and resistive heating, is the process by which the passage of an electric current through a conductor releases heat. It was first studied by James Prescott Joule in 1841. Joule immersed a length of wire in a fixed mass of water and measured the temperature...
in the wire. For a derivation that starts with Snell's law see Reitz page 454.
In plane waves
In a propagating sinusoidal linearly polarized electromagnetic plane wavePlane wave
In the physics of wave propagation, a plane wave is a constant-frequency wave whose wavefronts are infinite parallel planes of constant peak-to-peak amplitude normal to the phase velocity vector....
of a fixed frequency, the Poynting vector always points in the direction of propagation while oscillating in magnitude. The time-averaged magnitude of the Poynting vector is
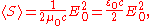
where
is the maximum amplitude of the electric field and is the speed of lightSpeed of light
The speed of light in vacuum, usually denoted by c, is a physical constant important in many areas of physics. Its value is 299,792,458 metres per second, a figure that is exact since the length of the metre is defined from this constant and the international standard for time...
in free space. This time-averaged value is also called the irradiance
Irradiance
Irradiance is the power of electromagnetic radiation per unit area incident on a surface. Radiant emittance or radiant exitance is the power per unit area radiated by a surface. The SI units for all of these quantities are watts per square meter , while the cgs units are ergs per square centimeter...
or intensity I.
Derivation
In an electromagnetic plane wave, and are always perpendicular to each other and the direction of propagation. Moreover, their amplitudes are related according to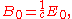and their time and position dependences are
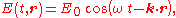
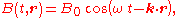
where
is the frequency of the wave and is wave vectorWave vector
In physics, a wave vector is a vector which helps describe a wave. Like any vector, it has a magnitude and direction, both of which are important: Its magnitude is either the wavenumber or angular wavenumber of the wave , and its direction is ordinarily the direction of wave propagation In...
.
The time-dependent and position magnitude of the Poynting vector is then
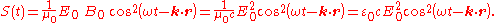
In the last step, we used the equality
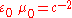. Since the time- or space-average of 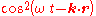is , it follows that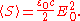Radiation pressure
S divided by the square of the speed of light in free space is the density of the linear momentum of the electromagnetic field. The time-averaged intensity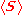 divided by the speed of light in free space is the radiation pressureRadiation pressure
Radiation pressure is the pressure exerted upon any surface exposed to electromagnetic radiation. If absorbed, the pressure is the power flux density divided by the speed of light...
exerted by an electromagnetic wave on the surface of a target:
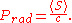
Further reading
- "Poynting Vector" from ScienceWorld (A Wolfram Web Resource) by Eric W. Weisstein