Fock state
Encyclopedia
A Fock state in quantum mechanics
, is any element of a Fock space
with a well-defined number of particle
s (or quanta
). These states are named after the Soviet physicist, V. A. Fock.
. Elements of a Fock space which are superpositions of states of differing particle number
(and thus not eigenstates of the number operator) are, therefore, not Fock states. Thus, not all elements of a Fock space are referred to as "Fock states."
If we limit to a single mode for simplicity (doing so we formally describe a mere harmonic oscillator
), a Fock state is of the type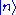
with n an integer value. This means that there are n quanta of excitation in the mode. 
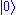corresponds to the ground state (no excitation). It is different from 0, which is the null vector.
Fock states form the most convenient basis
of the Fock space. They are defined to obey the following relations in the boson
ic algebra:
with
(resp. 
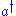) the annihilation (resp. creation) bose operator
. Similar relations hold for fermion
ic algebra.
This allows to check that
and 
, i.e., that measuring the number of particles 
in a Fock state returns always a definite value with no fluctuation.
of the field:
where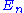
is the energy eigenvalue corresponding to 
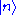. When we put in the expression for the Hamiltonian we get:
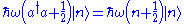
Therefore energy of the state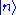
is given by 
where 
is the frequency of the field. Note that even at 
the energy does not vanish. This is the zero-point energy
.
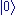is the state of lowest energy and the expectation values of 
and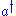 
vanish in this state:
The electrical and magnetic fields and the vector potential have the mode expansion of the same general form:
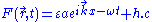
Thus it is easy to see that the expectation values of these field operators vanishes in the vacuum state:
However, it can be shown that the expectation values of the square of these field operators is non-zero. Thus there are fluctuations in the field about the zero ensemble average. These vacuum fluctuations are responsible for many interesting phenomenon including the Lamb shift in quantum optics.
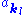and 
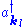will operate only on 
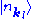. Since operators corresponding to different modes operate in different sub-spaces of the Hilbert space
, the entire field is a direct product of
over all the modes:
The creation and annihilation operators operate on the multi-mode state by only raising or lowering the number state of their own mode:
We also define the total number operator for the field which is a sum of number operators of each mode:
The multi-mode Fock state is an eigenvector of the total number operator whose eigenvalue is the total occupation number of all the modes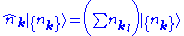
The multi-mode Fock states are also eigenstates of the multi-mode Hamiltonian
of these states in the representation is a 
'th derivative of the Dirac delta function
and therefore not a classical probability distribution.
Quantum mechanics
Quantum mechanics, also known as quantum physics or quantum theory, is a branch of physics providing a mathematical description of much of the dual particle-like and wave-like behavior and interactions of energy and matter. It departs from classical mechanics primarily at the atomic and subatomic...
, is any element of a Fock space
Fock space
The Fock space is an algebraic system used in quantum mechanics to describe quantum states with a variable or unknown number of particles. It is named after V. A...
with a well-defined number of particle
Elementary particle
In particle physics, an elementary particle or fundamental particle is a particle not known to have substructure; that is, it is not known to be made up of smaller particles. If an elementary particle truly has no substructure, then it is one of the basic building blocks of the universe from which...
s (or quanta
Quantum
In physics, a quantum is the minimum amount of any physical entity involved in an interaction. Behind this, one finds the fundamental notion that a physical property may be "quantized," referred to as "the hypothesis of quantization". This means that the magnitude can take on only certain discrete...
). These states are named after the Soviet physicist, V. A. Fock.
Definition
A more mathematical definition is that Fock states are those elements of a Fock space which are eigenstates of the particle number operatorParticle number operator
In quantum mechanics, for systems where the total number of particles may not be preserved, the number operator is the observable that counts the number of particles.The number operator acts on Fock space...
. Elements of a Fock space which are superpositions of states of differing particle number
Particle number
The particle number of a thermodynamic system, conventionally indicated with the letter N, is the number of constituent particles in that system. The particle number is a fundamental parameter in thermodynamics which is conjugate to the chemical potential. Unlike most physical quantities, particle...
(and thus not eigenstates of the number operator) are, therefore, not Fock states. Thus, not all elements of a Fock space are referred to as "Fock states."
If we limit to a single mode for simplicity (doing so we formally describe a mere harmonic oscillator
Harmonic oscillator
In classical mechanics, a harmonic oscillator is a system that, when displaced from its equilibrium position, experiences a restoring force, F, proportional to the displacement, x: \vec F = -k \vec x \, where k is a positive constant....
), a Fock state is of the type
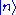with n an integer value. This means that there are n quanta of excitation in the mode. 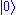corresponds to the ground state (no excitation). It is different from 0, which is the null vector.Fock states form the most convenient basis
Basis (linear algebra)
In linear algebra, a basis is a set of linearly independent vectors that, in a linear combination, can represent every vector in a given vector space or free module, or, more simply put, which define a "coordinate system"...
of the Fock space. They are defined to obey the following relations in the boson
Boson
In particle physics, bosons are subatomic particles that obey Bose–Einstein statistics. Several bosons can occupy the same quantum state. The word boson derives from the name of Satyendra Nath Bose....
ic algebra:
with
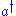(resp. ) the annihilation (resp. creation) bose operatorCreation and annihilation operators
Creation and annihilation operators are mathematical operators that have widespread applications in quantum mechanics, notably in the study of quantum harmonic oscillators and many-particle systems. An annihilation operator lowers the number of particles in a given state by one...
. Similar relations hold for fermion
Fermion
In particle physics, a fermion is any particle which obeys the Fermi–Dirac statistics . Fermions contrast with bosons which obey Bose–Einstein statistics....
ic algebra.
This allows to check that
and , i.e., that measuring the number of particles in a Fock state returns always a definite value with no fluctuation.Energy eigenstates
Fock states are eigenstates of the HamiltonianHamiltonian (quantum mechanics)
In quantum mechanics, the Hamiltonian H, also Ȟ or Ĥ, is the operator corresponding to the total energy of the system. Its spectrum is the set of possible outcomes when one measures the total energy of a system...
of the field:
where
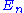is the energy eigenvalue corresponding to 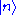. When we put in the expression for the Hamiltonian we get: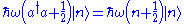Therefore energy of the state
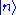is given by where is the frequency of the field. Note that even at the energy does not vanish. This is the zero-point energyZero-point energy
Zero-point energy is the lowest possible energy that a quantum mechanical physical system may have; it is the energy of its ground state. All quantum mechanical systems undergo fluctuations even in their ground state and have an associated zero-point energy, a consequence of their wave-like nature...
.
Vacuum fluctuations
The vacuum state or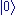 is the state of lowest energy and the expectation values of and 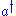vanish in this state:The electrical and magnetic fields and the vector potential have the mode expansion of the same general form:
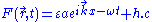
Thus it is easy to see that the expectation values of these field operators vanishes in the vacuum state:
However, it can be shown that the expectation values of the square of these field operators is non-zero. Thus there are fluctuations in the field about the zero ensemble average. These vacuum fluctuations are responsible for many interesting phenomenon including the Lamb shift in quantum optics.
Multi-mode Fock states
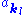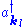In a multi-mode field each creation and annihilation operator operates on its own mode. So and will operate only on 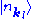. Since operators corresponding to different modes operate in different sub-spaces of the Hilbert spaceHilbert space
The mathematical concept of a Hilbert space, named after David Hilbert, generalizes the notion of Euclidean space. It extends the methods of vector algebra and calculus from the two-dimensional Euclidean plane and three-dimensional space to spaces with any finite or infinite number of dimensions...
, the entire field is a direct product of
over all the modes:The creation and annihilation operators operate on the multi-mode state by only raising or lowering the number state of their own mode:
We also define the total number operator for the field which is a sum of number operators of each mode:
The multi-mode Fock state is an eigenvector of the total number operator whose eigenvalue is the total occupation number of all the modes
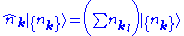
The multi-mode Fock states are also eigenstates of the multi-mode Hamiltonian
Non-classical behaviour
The Glauber-Sudarshan P-representation of Fock states shows that these states are purely quantum mechanical and have no classical counterpart. The of these states in the representation is a 'th derivative of the Dirac delta functionDirac delta function
The Dirac delta function, or δ function, is a generalized function depending on a real parameter such that it is zero for all values of the parameter except when the parameter is zero, and its integral over the parameter from −∞ to ∞ is equal to one. It was introduced by theoretical...
and therefore not a classical probability distribution.
External links
- Vladan Vuletic of MIT has used an ensemble of atoms to produce a Fock state (a.k.a single photon) source (PDF)
- Produce and measure a single photon state (Fock state) with an interactive experiment QuantumLab