Linear least squares - AbsoluteAstronomy.com

Statistics

Statistics is the study of the collection, organization, analysis, and interpretation of data. It deals with all aspects of this, including the planning of data collection in terms of the design of surveys and experiments....

and mathematics

Mathematics

Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...

, linear least squares is an approach to fitting a mathematical

Mathematical model

A mathematical model is a description of a system using mathematical concepts and language. The process of developing a mathematical model is termed mathematical modeling. Mathematical models are used not only in the natural sciences and engineering disciplines A mathematical model is a...

or statistical model

Statistical model

A statistical model is a formalization of relationships between variables in the form of mathematical equations. A statistical model describes how one or more random variables are related to one or more random variables. The model is statistical as the variables are not deterministically but...

to data

Data

The term data refers to qualitative or quantitative attributes of a variable or set of variables. Data are typically the results of measurements and can be the basis of graphs, images, or observations of a set of variables. Data are often viewed as the lowest level of abstraction from which...

in cases where the idealized value provided by the model for any data point is expressed linearly in terms of the unknown parameter

Parameter

Parameter from Ancient Greek παρά also “para” meaning “beside, subsidiary” and μέτρον also “metron” meaning “measure”, can be interpreted in mathematics, logic, linguistics, environmental science and other disciplines....

s of the model. The resulting fitted model can be used to summarize

Descriptive statistics

Descriptive statistics quantitatively describe the main features of a collection of data. Descriptive statistics are distinguished from inferential statistics , in that descriptive statistics aim to summarize a data set, rather than use the data to learn about the population that the data are...

the data, to predict

Prediction

A prediction or forecast is a statement about the way things will happen in the future, often but not always based on experience or knowledge...

unobserved values from the same system, and to understand the mechanisms that may underlie the system.

Mathematically, linear least squares is the problem of approximately solving an overdetermined system

Overdetermined system

In mathematics, a system of linear equations is considered overdetermined if there are more equations than unknowns. The terminology can be described in terms of the concept of counting constraints. Each unknown can be seen as an available degree of freedom...

of linear equations, where the best approximation is defined as that which minimizes the sum of squared differences between the data values and their corresponding modeled values. The approach is called "linear" least squares since the solution depends linearly on the data. Linear least squares problems are convex

Convex function

In mathematics, a real-valued function f defined on an interval is called convex if the graph of the function lies below the line segment joining any two points of the graph. Equivalently, a function is convex if its epigraph is a convex set...

and have a closed-form solution

Closed-form expression

In mathematics, an expression is said to be a closed-form expression if it can be expressed analytically in terms of a bounded number of certain "well-known" functions...

that is unique, provided that the number of data-points used for fitting equals or exceeds the number of unknown parameters, except in special degenerate situations. In contrast, non-linear least squares

Non-linear least squares

Non-linear least squares is the form of least squares analysis which is used to fit a set of m observations with a model that is non-linear in n unknown parameters . It is used in some forms of non-linear regression. The basis of the method is to approximate the model by a linear one and to...

problems generally must be solved by an iterative procedure

Iterative method

In computational mathematics, an iterative method is a mathematical procedure that generates a sequence of improving approximate solutions for a class of problems. A specific implementation of an iterative method, including the termination criteria, is an algorithm of the iterative method...

, and the problems can be non-convex with multiple optima for the objective function.

In statistics, linear least squares problems correspond to a particularly important type of statistical model

Statistical model

called linear regression

Linear regression

In statistics, linear regression is an approach to modeling the relationship between a scalar variable y and one or more explanatory variables denoted X. The case of one explanatory variable is called simple regression...

which arises as a particular form of regression analysis

Regression analysis

In statistics, regression analysis includes many techniques for modeling and analyzing several variables, when the focus is on the relationship between a dependent variable and one or more independent variables...

. One basic form of such a model is an ordinary least squares

Ordinary least squares

In statistics, ordinary least squares or linear least squares is a method for estimating the unknown parameters in a linear regression model. This method minimizes the sum of squared vertical distances between the observed responses in the dataset and the responses predicted by the linear...

model. The present article concentrates on the mathematical aspects of linear least squares problems, with discussion of the formulation and interpretation of statistical regression models, and of statistical inference

Statistical inference

In statistics, statistical inference is the process of drawing conclusions from data that are subject to random variation, for example, observational errors or sampling variation...

s related to these are dealt with in the articles just mentioned. See outline of regression analysis

Outline of regression analysis

In statistics, regression analysis includes any technique for learning about the relationship between one or more dependent variables Y and one or more independent variables X....

for an outline of the topic.

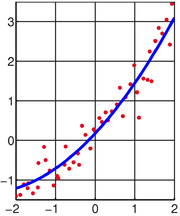
Motivational example

As a result of an experiment, four

data points were obtained,

and

(shown in red in the picture on the right). It is desired to find a line

that fits "best" these four points. In other words, we would like to find the numbers

and

that approximately solve the overdetermined linear system

of four equations in two unknowns in some "best" sense.

The least squares

Least squares

The method of least squares is a standard approach to the approximate solution of overdetermined systems, i.e., sets of equations in which there are more equations than unknowns. "Least squares" means that the overall solution minimizes the sum of the squares of the errors made in solving every...

approach to solving this problem is to try to make as small as possible the sum of squares of "errors" between the right- and left-hand sides of these equations, that is, to find the minimum

Maxima and minima

In mathematics, the maximum and minimum of a function, known collectively as extrema , are the largest and smallest value that the function takes at a point either within a given neighborhood or on the function domain in its entirety .More generally, the...

of the function

The minimum is determined by calculating the partial derivative

Partial derivative

In mathematics, a partial derivative of a function of several variables is its derivative with respect to one of those variables, with the others held constant...

s of

with respect to

and

and setting them to zero. This results in a system of two equations in two unknowns, called the normal equations, which give, when solved

and the equation

of the line of best fit. The residuals, that is, the discrepancies between the

values from the experiment and the

values calculated using the line of best fit are then found to be

and

(see the picture on the right). The minimum value of the sum of squares is

The general problem

Consider an overdetermined system

Overdetermined system

of m linear equation

Linear equation

A linear equation is an algebraic equation in which each term is either a constant or the product of a constant and a single variable....

s in n unknown coefficients, β₁,β₂,…,β_n, with m > n. This can be written in matrix

Matrix (mathematics)

In mathematics, a matrix is a rectangular array of numbers, symbols, or expressions. The individual items in a matrix are called its elements or entries. An example of a matrix with six elements isMatrices of the same size can be added or subtracted element by element...

form as

where

Such a system usually has no solution, so the goal is instead to find the coefficients β which fit the equations "best," in the sense of solving the quadratic

Quadratic

In mathematics, the term quadratic describes something that pertains to squares, to the operation of squaring, to terms of the second degree, or equations or formulas that involve such terms...

minimization problem

where the objective function S is given by

A justification for choosing this criterion is given in properties below. This minimization problem has a unique solution, provided that the n columns of the matrix X are linearly independent, given by solving the normal equations

Derivation of the normal equations

Define the

th residual to be

.

Then

can be rewritten

S is minimized

Maxima and minima

when its gradient vector is zero. (This follows by definition: if the gradient vector is not zero, there is a direction in which we can move to minimize it further - see maxima and minima

Maxima and minima

.) The elements of the gradient vector are the partial derivatives of S with respect to the parameters:

The derivatives are

Substitution of the expressions for the residuals and the derivatives into the gradient equations gives

Thus if

minimizes S, we have

Upon rearrangement, we obtain the normal equations:

The normal equations are written in matrix notation as

(where X^T is the matrix transpose of X)

The solution of the normal equations yields the vector

of the optimal parameter values.

Computation

A general approach to the least squares problem

can be described as follows. Suppose that we can find a n by m matrix S
such that XS is an
orthogonal projection onto the image of X. Then a solution to our minimization problem is given by

simply because

is exactly a sought for orthogonal projection of

onto an image of X
(see the picture below and note that as explained in the
next section the image of X is just a subspace generated by column vectors of X).
A few popular ways to find such a matrix S are described below.

Inverting the matrix of the normal equations

The algebraic solution of the normal equations can be written as

where X⁺ is the Moore–Penrose pseudoinverse of X. Although this equation is correct, and can work in many applications, it is not computationally efficient to invert the normal equations matrix. An exception occurs in numerical smoothing and differentiation

Numerical smoothing and differentiation

An experimental datum value can be conceptually described as the sum of a signal and some noise, but in practice the two contributions cannot be separated. The purpose of smoothing is to increase the Signal-to-noise ratio without greatly distorting the signal...

where an analytical expression is required.

If the matrix X^TX is well-conditioned

Condition number

In the field of numerical analysis, the condition number of a function with respect to an argument measures the asymptotically worst case of how much the function can change in proportion to small changes in the argument...

and positive definite

Positive-definite matrix

In linear algebra, a positive-definite matrix is a matrix that in many ways is analogous to a positive real number. The notion is closely related to a positive-definite symmetric bilinear form ....

, that is, it has full rank

Rank (linear algebra)

The column rank of a matrix A is the maximum number of linearly independent column vectors of A. The row rank of a matrix A is the maximum number of linearly independent row vectors of A...

, the normal equations can be solved directly by using the Cholesky decomposition

Cholesky decomposition

In linear algebra, the Cholesky decomposition or Cholesky triangle is a decomposition of a Hermitian, positive-definite matrix into the product of a lower triangular matrix and its conjugate transpose. It was discovered by André-Louis Cholesky for real matrices...

R^TR, where R is an upper triangular matrix

Triangular matrix

In the mathematical discipline of linear algebra, a triangular matrix is a special kind of square matrix where either all the entries below or all the entries above the main diagonal are zero...

, giving:

The solution is obtained in two stages, a forward substitution step, solving for z:

followed by a backward substitution, solving for

Both substitutions are facilitated by the triangular nature of R.

See example of linear regression for a worked-out numerical example with three parameters.

Orthogonal decomposition methods

Orthogonal decomposition methods of solving the least squares problem are slower than the normal equations method but are more numerically stable

Numerical stability

In the mathematical subfield of numerical analysis, numerical stability is a desirable property of numerical algorithms. The precise definition of stability depends on the context, but it is related to the accuracy of the algorithm....

, from not having to form the product X^TX.

The residuals are written in matrix notation as

The matrix X is subjected to an orthogonal decomposition; the QR decomposition

QR decomposition

In linear algebra, a QR decomposition of a matrix is a decomposition of a matrix A into a product A=QR of an orthogonal matrix Q and an upper triangular matrix R...

will serve to illustrate the process.

where Q is an m×m orthogonal matrix

Orthogonal matrix

In linear algebra, an orthogonal matrix , is a square matrix with real entries whose columns and rows are orthogonal unit vectors ....

and R is an m×n matrix which is partitioned

Block matrix

In the mathematical discipline of matrix theory, a block matrix or a partitioned matrix is a matrix broken into sections called blocks. Looking at it another way, the matrix is written in terms of smaller matrices. We group the rows and columns into adjacent 'bunches'. A partition is the rectangle...

into a n×n upper triangular

Triangular matrix

In the mathematical discipline of linear algebra, a triangular matrix is a special kind of square matrix where either all the entries below or all the entries above the main diagonal are zero...

block, R_n, and a (m − n)×n zero block 0.

The residual vector is left-multiplied by Q^T.

Because Q is orthogonal

Orthogonal matrix

In linear algebra, an orthogonal matrix , is a square matrix with real entries whose columns and rows are orthogonal unit vectors ....

, the sum of squares of the residuals, s, may be written as:

Since v doesn't depend on β, the minimum value of s is attained when the upper block, u, is zero. Therefore the parameters are found by solving:

These equations are easily solved as R_n is upper triangular.

An alternative decomposition of X is the singular value decomposition

Singular value decomposition

In linear algebra, the singular value decomposition is a factorization of a real or complex matrix, with many useful applications in signal processing and statistics....

(SVD)

where U is m by m orthogonal matrix, V is n by n orthogonal matrix and

is an m by n matrix with all its elements outside of the main diagonal equal to 0. The (pseudo)-inverse of

is easily obtained by inverting its non-zero diagonal elements. Hence,

where P is obtained from

by replacing its non-zero diagonal elements with ones. Since X and

are obviously of the same rank (one of the many advantages of singular value decomposition

Singular value decomposition

In linear algebra, the singular value decomposition is a factorization of a real or complex matrix, with many useful applications in signal processing and statistics....

)

is an orthogonal projection onto the image (column-space) of X and in accordance with a general approach described in the introduction above,

is a solution of a least squares problem. This method is the most computationally intensive, but is particularly useful if the normal equations matrix, X^TX, is very ill-conditioned (i.e. if its condition number

Condition number

multiplied by the machine's relative round-off error

Round-off error

A round-off error, also called rounding error, is the difference between the calculated approximation of a number and its exact mathematical value. Numerical analysis specifically tries to estimate this error when using approximation equations and/or algorithms, especially when using finitely many...

is appreciably large). In that case, including the smallest singular values in the inversion merely adds numerical noise to the solution. This can be cured using the truncated SVD approach, giving a more stable and exact answer, by explicitly setting to zero all singular values below a certain threshold and so ignoring them, a process closely related to factor analysis

Factor analysis

Factor analysis is a statistical method used to describe variability among observed, correlated variables in terms of a potentially lower number of unobserved, uncorrelated variables called factors. In other words, it is possible, for example, that variations in three or four observed variables...

Properties of the least-squares estimators

The gradient equations at the minimum can be written as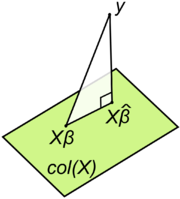

A geometrical interpretation of these equations is that the vector of residuals,

is orthogonal to the column space

Column space

In linear algebra, the column space of a matrix is the set of all possible linear combinations of its column vectors. The column space of an m × n matrix is a subspace of m-dimensional Euclidean space...

of X, since the dot product

is equal to zero for any conformal vector, v. This means that

is the shortest of all possible vectors

, that is, the variance of the residuals is the minimum possible. This is illustrated at the right.

Introducing

and a matrix K with the assumption that a matrix

is non-sigular and K^T X = 0 (cf. Orthogonal projections), the residual vector should satisfy the following equation:

The equation and solution of linear least squares are thus described as follows:

If the experimental errors,

, are uncorrelated, have a mean of zero and a constant variance,

, the Gauss-Markov theorem states that the least-squares estimator,

, has the minimum variance of all estimators that are linear combinations of the observations. In this sense it is the best, or optimal, estimator of the parameters. Note particularly that this property is independent of the statistical distribution function

Distribution function

In molecular kinetic theory in physics, a particle's distribution function is a function of seven variables, f, which gives the number of particles per unit volume in phase space. It is the number of particles per unit volume having approximately the velocity near the place and time...

of the errors. In other words, the distribution function of the errors need not be a normal distribution. However, for some probability distributions, there is no guarantee that the least-squares solution is even possible given the observations; still, in such cases it is the best estimator that is both linear and unbiased.

For example, it is easy to show that the arithmetic mean

Arithmetic mean

In mathematics and statistics, the arithmetic mean, often referred to as simply the mean or average when the context is clear, is a method to derive the central tendency of a sample space...

of a set of measurements of a quantity is the least-squares estimator of the value of that quantity. If the conditions of the Gauss-Markov theorem apply, the arithmetic mean is optimal, whatever the distribution of errors of the measurements might be.

However, in the case that the experimental errors do belong to a normal distribution, the least-squares estimator is also a maximum likelihood

Maximum likelihood

In statistics, maximum-likelihood estimation is a method of estimating the parameters of a statistical model. When applied to a data set and given a statistical model, maximum-likelihood estimation provides estimates for the model's parameters....

estimator.

These properties underpin the use of the method of least squares for all types of data fitting, even when the assumptions are not strictly valid.

Limitations

An assumption underlying the treatment given above is that the independent variable, x, is free of error. In practice, the errors on the measurements of the independent variable are usually much smaller than the errors on the dependent variable and can therefore be ignored. When this is not the case, total least squares also known as Errors-in-variables models
Errors-in-variables models
In statistics and econometrics, errors-in-variables models or measurement errors models are regression models that account for measurement errors in the independent variables...

, or Rigorous least squares, should be used. This can be done by adjusting the weighting scheme to take into account errors on both the dependent and independent variables and then following the standard procedure.

In some cases the (weighted) normal equations matrix X^TX is ill-conditioned. When fitting polynomials the normal equations matrix is a Vandermonde matrix. Vandermode matrices become increasingly ill-conditioned as the order of the matrix increases. In these cases, the least squares estimate amplifies the measurement noise and may be grossly inaccurate. Various regularization

Regularization (mathematics)

In mathematics and statistics, particularly in the fields of machine learning and inverse problems, regularization involves introducing additional information in order to solve an ill-posed problem or to prevent overfitting...

techniques can be applied in such cases, the most common of which is called ridge regression

Tikhonov regularization

Tikhonov regularization, named for Andrey Tikhonov, is the most commonly used method of regularization of ill-posed problems. In statistics, the method is known as ridge regression, and, with multiple independent discoveries, it is also variously known as the Tikhonov-Miller method, the...

. If further information about the parameters is known, for example, a range of possible values of

, then various techniques can be used to increase the stability of the solution. For example, see constrained least squares.

Another drawback of the least squares estimator is the fact that the norm of the residuals,

is minimized, whereas in some cases one is truly interested in obtaining small error in the parameter

, e.g., a small value of

. However, since

is unknown, this quantity cannot be directly minimized. If a prior probability

Prior probability

In Bayesian statistical inference, a prior probability distribution, often called simply the prior, of an uncertain quantity p is the probability distribution that would express one's uncertainty about p before the "data"...

is known, then a Bayes estimator

Bayes estimator

In estimation theory and decision theory, a Bayes estimator or a Bayes action is an estimator or decision rule that minimizes the posterior expected value of a loss function . Equivalently, it maximizes the posterior expectation of a utility function...

can be used to minimize the mean squared error

Mean squared error

In statistics, the mean squared error of an estimator is one of many ways to quantify the difference between values implied by a kernel density estimator and the true values of the quantity being estimated. MSE is a risk function, corresponding to the expected value of the squared error loss or...

. The least squares method is often applied when no prior is known. Surprisingly, when several parameters are being estimated jointly, better estimators can be constructed, an effect known as Stein's phenomenon. For example, if the measurement error is Gaussian, several estimators are known which dominate

Dominating decision rule

In decision theory, a decision rule is said to dominate another if the performance of the former is sometimes better, and never worse, than that of the latter....

, or outperform, the least squares technique; the best known of these is the James–Stein estimator. This is an example of more general shrinkage estimator

Shrinkage estimator

In statistics, a shrinkage estimator is an estimator that, either explicitly or implicitly, incorporates the effects of shrinkage. In loose terms this means that a naïve or raw estimate is improved by combining it with other information. The term relates to the notion that the improved estimate is...

s that have been applied to regression problems.

Weighted linear least squares

In some cases the observations may be weighted—for example, they may not be equally reliable. In this case, one can minimize the weighted sum of squares:

where w_i > 0 is the weight of the ith observation, and W is the diagonal matrix

Diagonal matrix

In linear algebra, a diagonal matrix is a matrix in which the entries outside the main diagonal are all zero. The diagonal entries themselves may or may not be zero...

of such weights.

The weights should, ideally, be equal to the reciprocal

Multiplicative inverse

In mathematics, a multiplicative inverse or reciprocal for a number x, denoted by 1/x or x−1, is a number which when multiplied by x yields the multiplicative identity, 1. The multiplicative inverse of a fraction a/b is b/a. For the multiplicative inverse of a real number, divide 1 by the...

of the variance

Variance

In probability theory and statistics, the variance is a measure of how far a set of numbers is spread out. It is one of several descriptors of a probability distribution, describing how far the numbers lie from the mean . In particular, the variance is one of the moments of a distribution...

of the measurement.
The normal equations are then:

This method is used in iteratively reweighted least squares.

Parameter errors, correlation and confidence limits

The estimated parameter values are linear combinations of the observed values

Therefore an expression for the residuals (i.e., the estimated errors in the observations) can be obtained by error propagation from the errors in the observations. Let the variance-covariance matrix for the observations be denoted by M and that of the parameters by M^β. Then,

When W = M⁻¹ this simplifies to

When unit weights are used (W = I) it is implied that the experimental errors are uncorrelated and all equal: M = σ²I, where σ² is the variance of an observation, and I is the identity matrix

Identity matrix

In linear algebra, the identity matrix or unit matrix of size n is the n×n square matrix with ones on the main diagonal and zeros elsewhere. It is denoted by In, or simply by I if the size is immaterial or can be trivially determined by the context...

. In this case σ² is approximated by

, where S is the minimum value of the objective function

The denominator, m-n, is the statistical degrees of freedom

Degrees of freedom (statistics)

In statistics, the number of degrees of freedom is the number of values in the final calculation of a statistic that are free to vary.Estimates of statistical parameters can be based upon different amounts of information or data. The number of independent pieces of information that go into the...

; see effective degrees of freedom for generalizations for the case of correlated observations. In all cases, the variance

Variance

of the parameter

is given by

and the covariance

Covariance

In probability theory and statistics, covariance is a measure of how much two variables change together. Variance is a special case of the covariance when the two variables are identical.- Definition :...

between parameters

and

is given by

. Standard deviation

Standard deviation

Standard deviation is a widely used measure of variability or diversity used in statistics and probability theory. It shows how much variation or "dispersion" there is from the average...

is the square root of variance and the correlation coefficient is given by

. These error estimates reflect only random errors in the measurements. The true uncertainty in the parameters is larger due to the presence of systematic errors which, by definition, cannot be quantified.
Note that even though the observations may be un-correlated, the parameters are always correlated

Pearson product-moment correlation coefficient

In statistics, the Pearson product-moment correlation coefficient is a measure of the correlation between two variables X and Y, giving a value between +1 and −1 inclusive...

.

It is often assumed, for want of any concrete evidence, that the error on an observation belongs to a normal distribution with a mean of zero and standard deviation

. Under that assumption the following probabilities can be derived.

68% within the interval

95% within the interval

99% within the interval

The assumption is not unreasonable when m >> n. If the experimental errors are normally distributed the parameters will belong to a Student's t-distribution with m − n degrees of freedom

Degrees of freedom (statistics)

. When m >> n Student's t-distribution approximates to a Normal distribution. Note, however, that these confidence limits cannot take systematic error into account. Also, parameter errors should be quoted to one significant figure only, as they are subject to sampling error

Sampling error

-Random sampling:In statistics, sampling error or estimation error is the error caused by observing a sample instead of the whole population. The sampling error can be found by subtracting the value of a parameter from the value of a statistic...

.

When the number of observations is relatively small, Chebychev's inequality can be used for an upper bound on probabilities, regardless of any assumptions about the distribution of experimental errors: the maximum probabilities that a parameter will be more than 1, 2 or 3 standard deviations away from its expectation value are 100%, 25% and 11% respectively.

Residual values and correlation

The residuals

Errors and residuals in statistics

In statistics and optimization, statistical errors and residuals are two closely related and easily confused measures of the deviation of a sample from its "theoretical value"...

are related to the observations by

where H is the symmetric, idempotent matrix

Idempotent matrix

In algebra, an idempotent matrix is a matrix which, when multiplied by itself, yields itself. That is, the matrix M is idempotent if and only if MM = M...

known as the hat matrix

Hat matrix

In statistics, the hat matrix, H, maps the vector of observed values to the vector of fitted values. It describes the influence each observed value has on each fitted value...

and I is the identity matrix

Identity matrix

. The variance-covariance matrice of the residuals, M^r is given by

Thus the residuals are correlated, even if the observations are not.

When

The sum of residual values is equal to zero whenever the model function contains a constant term. Left-multiply the expression for the residuals by X^T:

Say, for example, that the first term of the model is a constant, so that

for all i. In that case it follows that

Thus, in the motivational example, above, the fact that the sum of residual values is equal to zero it is not accidental but is a consequence of the presence of the constant term, α, in the model.

If experimental error follows a normal distribution, then, because of the linear relationship between residuals and observations, so should residuals, but since the observations are only a sample of the population of all possible observations, the residuals should belong to a Student's t-distribution. Studentized residual

Studentized residual

In statistics, a studentized residual is the quotient resulting from the division of a residual by an estimate of its standard deviation. Typically the standard deviations of residuals in a sample vary greatly from one data point to another even when the errors all have the same standard...

s are useful in making a statistical test for an outlier

Outlier

In statistics, an outlier is an observation that is numerically distant from the rest of the data. Grubbs defined an outlier as: An outlying observation, or outlier, is one that appears to deviate markedly from other members of the sample in which it occurs....

when a particular residual appears to be excessively large.

Objective function

The objective function can be written as

since (I – H) is also symmetric and idempotent. It can be shown from this, that the expected value

Expected value

In probability theory, the expected value of a random variable is the weighted average of all possible values that this random variable can take on...

of S is m-n. Note, however, that this is true only if the weights have been assigned correctly. If unit weights are assumed, the expected value of S is

, where

is the variance of an observation.

If it is assumed that the residuals belong to a Normal distribution, the objective function, being a sum of weighted squared residuals, will belong to a Chi-squared (

) distribution with m-n degrees of freedom

Degrees of freedom (statistics)

. Some illustrative percentile values of

are given in the following table.

m-n
10	9.34	18.3	23.2
25	24.3	37.7	44.3
100	99.3	124	136

These values can be used for a statistical criterion as to the goodness-of-fit. When unit weights are used, the numbers should be divided by the variance of an observation.

Constrained linear least squares

Often it is of interest to solve a linear least squares problem with an additional constraint on the solution. With constrained linear least squares, the original equation

must be satisfied (in the least squares sense) while also ensuring that some other property of

is maintained. There are often special purpose algorithms for solving such problems efficiently. Some examples of constraints are given below:

Equality constrained
Constrained generalized inverse
A constrained generalized inverse inverse is obtained by solving a system of linear equations with an additional constraint that the solution is in a given subspace...

least squares: the elements of must exactly satisfy
Regularized
Tikhonov regularization
Tikhonov regularization, named for Andrey Tikhonov, is the most commonly used method of regularization of ill-posed problems. In statistics, the method is known as ridge regression, and, with multiple independent discoveries, it is also variously known as the Tikhonov-Miller method, the...

least squares: the elements of must satisfy
Non-negative least squares (NNLS): The vector satisfies the vector inequality
Ordered vector space
In mathematics an ordered vector space or partially ordered vector space is a vector space equipped with a partial order which is compatible with the vector space operations.- Definition:...

that is defined componentwise --- that is, each component must be either positive or zero.
Box-constrained least squares: The vector satisfies the vector inequalities
Ordered vector space
In mathematics an ordered vector space or partially ordered vector space is a vector space equipped with a partial order which is compatible with the vector space operations.- Definition:...

, each of which is defined componentwise.
Integer constrained least squares: all elements of must be integer
Integer
The integers are formed by the natural numbers together with the negatives of the non-zero natural numbers .They are known as Positive and Negative Integers respectively...

(instead of real number
Real number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...

s).
Real constrained least squares: all elements of must be real (rather than complex number
Complex number
A complex number is a number consisting of a real part and an imaginary part. Complex numbers extend the idea of the one-dimensional number line to the two-dimensional complex plane by using the number line for the real part and adding a vertical axis to plot the imaginary part...

s).
Phase constrained least squares: all elements of must have the same phase
Arg (mathematics)
In mathematics, arg is a function operating on complex numbers . It gives the angle between the line joining the point to the origin and the positive real axis, shown as in figure 1 opposite, known as an argument of the point In mathematics, arg is a function operating on complex numbers...

.

When the constraint only applies to some of the variables, the mixed problem may be solved using separable least squares by letting

and

represent the unconstrained (1) and constrained (2) components. Then substituting the least squares solution for

, i.e.

back into the original expression gives (following some rearrangement) an equation that can be solved as a purely constrained problem in

where

is a projection matrix. Following the constrained estimation of

the vector

is obtained from the expression above.

Typical uses and applications

Polynomial fitting
Polynomial regression
In statistics, polynomial regression is a form of linear regression in which the relationship between the independent variable x and the dependent variable y is modeled as an nth order polynomial...

: models are polynomial
Polynomial
In mathematics, a polynomial is an expression of finite length constructed from variables and constants, using only the operations of addition, subtraction, multiplication, and non-negative integer exponents...

s in an independent variable, x:
- Straight line: .
- Quadratic: .
- Cubic, quartic and higher polynomials. For regression with high-order polynomials
  Polynomial regression
  In statistics, polynomial regression is a form of linear regression in which the relationship between the independent variable x and the dependent variable y is modeled as an nth order polynomial...
  
  , the use of orthogonal polynomials
  Orthogonal polynomials
  In mathematics, the classical orthogonal polynomials are the most widely used orthogonal polynomials, and consist of the Hermite polynomials, the Laguerre polynomials, the Jacobi polynomials together with their special cases the ultraspherical polynomials, the Chebyshev polynomials, and the...
  
  is recommended.
Numerical smoothing and differentiation
Numerical smoothing and differentiation
An experimental datum value can be conceptually described as the sum of a signal and some noise, but in practice the two contributions cannot be separated. The purpose of smoothing is to increase the Signal-to-noise ratio without greatly distorting the signal...

— this is an application of polynomial fitting.
Multinomials in more than one independent variable, including surface fitting
Curve fitting with B-spline
B-spline
In the mathematical subfield of numerical analysis, a B-spline is a spline function that has minimal support with respect to a given degree, smoothness, and domain partition. B-splines were investigated as early as the nineteenth century by Nikolai Lobachevsky...

s
Chemometrics
Chemometrics
Chemometrics is the science of extracting information from chemical systems by data-driven means. It is a highly interfacial discipline, using methods frequently employed in core data-analytic disciplines such as multivariate statistics, applied mathematics, and computer science, in order to...

, Calibration curve
Calibration curve
In analytical chemistry, a calibration curve is a general method for determining the concentration of a substance in an unknown sample by comparing the unknown to a set of standard samples of known concentration...

, Standard addition
Standard Addition
The method of standard addition is used in instrumental analysis to determine concentration of a substance in an unknown sample by comparison to a set of samples of known concentration, similar to using a calibration curve...

, Gran plot
Gran plot
A Gran plot is a common means of standardizing a titrate or titrant by estimating the equivalence volume or end point in a strong acid-strong base titration or in a potentiometric titration...

, analysis of mixtures

Uses in data fitting

The primary application of linear least squares is in data fitting. Given a set of m data points

consisting of experimentally measured values taken at m values

of an independent variable (

may be scalar or vector quantities), and given a model function

with

it is desired to find the parameters

such that the model function "best" fits the data. In linear least squares, linearity is meant to be with respect to parameters

Here, the functions

may be nonlinear with respect to the variable x.

Ideally, the model function fits the data exactly, so

for all

This is usually not possible in practice, as there are more data points than there are parameters to be determined. The approach chosen then is to find the minimal possible value of the sum of squares of the residuals

so to minimize the function

After substituting for

and then for

, this minimization problem becomes the quadratic minimization problem above with

and the best fit can be found by solving the normal equations.

Further Discussion

The numerical methods for linear least squares are important because linear regression

Linear regression

models are among the most important types of model, both as formal statistical model

Statistical model

s and for exploration of data-sets. The majority of statistical computer packages

Comparison of statistical packages

The following tables compare general and technical information for a number of statistical analysis packages.-General information:Basic information about each product...

contain facilities for regression analysis that make use of linear least squares computations. Hence it is appropriate that considerable effort has been devoted to the task of ensuring that these computations are undertaken efficiently and with due regard to round-off error

Round-off error

.

Individual statistical analyses are seldom undertaken in isolation, but rather are part of a sequence of investigatory steps. Some of the topics involved in considering numerical methods for linear least squares relate to this point. Thus important topics can be

Computations where a number of similar, and often nested, models are considered for the same data-set. That is, where models with the same dependent variable but different sets of independent variables are to be considered, for essentially the same set of data-points.
Computations for analyses that occur in a sequence, as the number of data-points increases.
Special considerations for very extensive data-sets.

Fitting of linear models by least squares often, but not always, arise in the context of statistical analysis. It can therefore be important that considerations of computation efficiency for such problems extend to all of the auxiliary quantities required for such analyses, and are not restricted to the formal solution of the linear least squares problem.

Rounding errors

Matrix calculations, like any other, are affected by rounding errors. An early summary of these effects, regarding the choice of computation methods for matrix inversion, was provided by Wilkinson.

External links

Theory

Online utilities

Online Linear Least Squares Utility

The source of this article is wikipedia, the free encyclopedia. The text of this article is licensed under the GFDL.