Dominating decision rule
Encyclopedia
In decision theory
, a decision rule is said to dominate another if the performance of the former is sometimes better, and never worse, than that of the latter.
Formally, let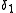
and 
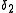be two decision rules
, and let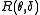
be the risk
of rule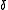
for parameter 
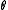. The decision rule 
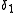is said to dominate the rule 
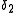if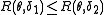 
for all 
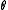, and the inequality is strict for some 
.
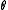This defines a partial order on decision rules; the maximal element
s with respect to this order are called admissible decision rule
s.
Decision theory
Decision theory in economics, psychology, philosophy, mathematics, and statistics is concerned with identifying the values, uncertainties and other issues relevant in a given decision, its rationality, and the resulting optimal decision...
, a decision rule is said to dominate another if the performance of the former is sometimes better, and never worse, than that of the latter.
Formally, let
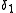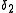and be two decision rulesDecision theory
Decision theory in economics, psychology, philosophy, mathematics, and statistics is concerned with identifying the values, uncertainties and other issues relevant in a given decision, its rationality, and the resulting optimal decision...
, and let
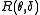be the riskRisk function
In decision theory and estimation theory, the risk function R of a decision rule, δ, is the expected value of a loss function L:...
of rule
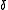for parameter 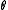. The decision rule 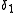is said to dominate the rule 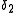if 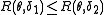for all 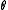, and the inequality is strict for some 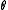.This defines a partial order on decision rules; the maximal element
Maximal element
In mathematics, especially in order theory, a maximal element of a subset S of some partially ordered set is an element of S that is not smaller than any other element in S. The term minimal element is defined dually...
s with respect to this order are called admissible decision rule
Admissible decision rule
In statistical decision theory, an admissible decision rule is a rule for making a decision such that there isn't any other rule that is always "better" than it, in a specific sense defined below....
s.