Idempotent matrix
Encyclopedia
In algebra
, an idempotent matrix is a matrix
which, when multiplied by itself, yields itself. That is, the matrix M is idempotent if and only if MM = M. For this product MM to be conformable for multiplication
, M must necessarily be a square matrix.
, an idempotent matrix is singular; that is, its number of independent rows (and columns) is less than its number of rows (and columns). This can be seen from writing MM = M, assuming that M has full rank (is non-singular), and pre-multiplying by M−1 to obtain M = M−1M = I.
When an idempotent matrix is subtracted from the identity matrix, the result is also idempotent. This holds since [I − M][I − M] = I − M − M + M2 = I − M − M + M = I − M.
An idempotent matrix is always diagonalizable and its eigenvalues are either 0 or 1. The trace
of an idempotent matrix — the sum of the elements on its main diagonal — equals the rank
of the matrix and thus is always an integer. This provides an easy way of computing the rank, or alternatively an easy way of determining the trace of a matrix whose elements are not specifically known (which is helpful in econometrics
, for example, in establishing the degree of bias
in using a sample variance
as an estimate of a population variance
).
and econometrics
. For example, in ordinary least squares
, the regression problem is to choose a vector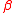
of coefficient estimates so as to minimize the sum of squared residuals (mispredictions) ei: in matrix form,
where y is a vector of dependent variable observations, and X is a matrix each of whose columns is a column of observations on one of the independent variables. The resulting estimator is
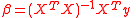
where superscript T indicates a transpose
, and the vector of residuals is
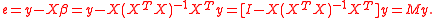
Here both M and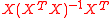
are idempotent matrices, a fact which allows simplification when the sum of squared residuals is computed:
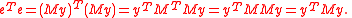
The idempotency of M plays a role in other calculations as well, such as in determining the variance of the estimator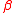
.
Algebra
Algebra is the branch of mathematics concerning the study of the rules of operations and relations, and the constructions and concepts arising from them, including terms, polynomials, equations and algebraic structures...
, an idempotent matrix is a matrix
Matrix (mathematics)
In mathematics, a matrix is a rectangular array of numbers, symbols, or expressions. The individual items in a matrix are called its elements or entries. An example of a matrix with six elements isMatrices of the same size can be added or subtracted element by element...
which, when multiplied by itself, yields itself. That is, the matrix M is idempotent if and only if MM = M. For this product MM to be conformable for multiplication
Matrix multiplication
In mathematics, matrix multiplication is a binary operation that takes a pair of matrices, and produces another matrix. If A is an n-by-m matrix and B is an m-by-p matrix, the result AB of their multiplication is an n-by-p matrix defined only if the number of columns m of the left matrix A is the...
, M must necessarily be a square matrix.
Properties
With the exception of the identity matrixIdentity matrix
In linear algebra, the identity matrix or unit matrix of size n is the n×n square matrix with ones on the main diagonal and zeros elsewhere. It is denoted by In, or simply by I if the size is immaterial or can be trivially determined by the context...
, an idempotent matrix is singular; that is, its number of independent rows (and columns) is less than its number of rows (and columns). This can be seen from writing MM = M, assuming that M has full rank (is non-singular), and pre-multiplying by M−1 to obtain M = M−1M = I.
When an idempotent matrix is subtracted from the identity matrix, the result is also idempotent. This holds since [I − M][I − M] = I − M − M + M2 = I − M − M + M = I − M.
An idempotent matrix is always diagonalizable and its eigenvalues are either 0 or 1. The trace
Trace (linear algebra)
In linear algebra, the trace of an n-by-n square matrix A is defined to be the sum of the elements on the main diagonal of A, i.e.,...
of an idempotent matrix — the sum of the elements on its main diagonal — equals the rank
Rank (linear algebra)
The column rank of a matrix A is the maximum number of linearly independent column vectors of A. The row rank of a matrix A is the maximum number of linearly independent row vectors of A...
of the matrix and thus is always an integer. This provides an easy way of computing the rank, or alternatively an easy way of determining the trace of a matrix whose elements are not specifically known (which is helpful in econometrics
Econometrics
Econometrics has been defined as "the application of mathematics and statistical methods to economic data" and described as the branch of economics "that aims to give empirical content to economic relations." More precisely, it is "the quantitative analysis of actual economic phenomena based on...
, for example, in establishing the degree of bias
Bias (statistics)
A statistic is biased if it is calculated in such a way that it is systematically different from the population parameter of interest. The following lists some types of, or aspects of, bias which should not be considered mutually exclusive:...
in using a sample variance
Variance
In probability theory and statistics, the variance is a measure of how far a set of numbers is spread out. It is one of several descriptors of a probability distribution, describing how far the numbers lie from the mean . In particular, the variance is one of the moments of a distribution...
as an estimate of a population variance
Variance
In probability theory and statistics, the variance is a measure of how far a set of numbers is spread out. It is one of several descriptors of a probability distribution, describing how far the numbers lie from the mean . In particular, the variance is one of the moments of a distribution...
).
Applications
Idempotent matrices arise frequently in regression analysisRegression analysis
In statistics, regression analysis includes many techniques for modeling and analyzing several variables, when the focus is on the relationship between a dependent variable and one or more independent variables...
and econometrics
Econometrics
Econometrics has been defined as "the application of mathematics and statistical methods to economic data" and described as the branch of economics "that aims to give empirical content to economic relations." More precisely, it is "the quantitative analysis of actual economic phenomena based on...
. For example, in ordinary least squares
Ordinary least squares
In statistics, ordinary least squares or linear least squares is a method for estimating the unknown parameters in a linear regression model. This method minimizes the sum of squared vertical distances between the observed responses in the dataset and the responses predicted by the linear...
, the regression problem is to choose a vector
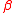of coefficient estimates so as to minimize the sum of squared residuals (mispredictions) ei: in matrix form,where y is a vector of dependent variable observations, and X is a matrix each of whose columns is a column of observations on one of the independent variables. The resulting estimator is
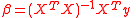
where superscript T indicates a transpose
Transpose
In linear algebra, the transpose of a matrix A is another matrix AT created by any one of the following equivalent actions:...
, and the vector of residuals is
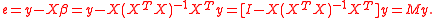
Here both M and
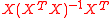are idempotent matrices, a fact which allows simplification when the sum of squared residuals is computed: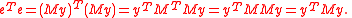The idempotency of M plays a role in other calculations as well, such as in determining the variance of the estimator
.
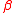