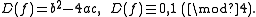Binary quadratic form
Encyclopedia
In mathematics
, a binary quadratic form is a quadratic form
in two variables. More concretely, it is a homogeneous polynomial
of degree 2 in two variables
where a, b, c are the coefficients. Properties of binary quadratic forms depend in an essential way on the nature of the coefficients, which may be real number
s, rational number
s, or in the most delicate case, integer
s. Arithmetical aspects of the theory of binary quadratic forms are related to the arithmetic of quadratic field
s and have been much studied, notably, by Gauss
in Section V of Disquisitiones Arithmeticae
. The theory of binary quadratic forms has been extended in two directions: general number fields and quadratic forms in n variables.
may be viewed as a part of the theory of binary quadratic forms. Lagrange
in 1773 initiated the development of the general theory of quadratic forms. First systematic treatment of binary quadratic forms is due to Legendre
. Their theory was advanced much further by Gauss
in Disquisitiones Arithmeticae
. He considered questions of equivalence and reduction and introduced composition of binary quadratic forms (Gauss and many subsequent authors wrote 2b in place of b; the modern convention allowing the coefficient of xy to be odd is due to Eisenstein). These investigations of Gauss strongly influenced both the arithmetical theory of quadratic forms in more than two variables and the subsequent development of algebraic number theory, where quadratic fields are replaced with more general number fields.
Two integral forms are called equivalent if there exists an invertible integral linear change of variables that transforms the first form into the second. This defines an equivalence relation
on the set of integral quadratic forms, whose elements are called classes of quadratic forms. Equivalent forms necessarily have the same discriminant
Gauss proved that for every value D, there are only finitely many classes of binary quadratic forms with discriminant D. Their number is the class number of discriminant D. He described an algorithm, called reduction, for constructing a canonical representative in each class, the reduced form, whose coefficients are the smallest in a suitable sense. One of the deepest discoveries of Gauss was the existence of a natural composition law on the set of classes of binary quadratic forms of given discriminant, which makes this set into a finite abelian group
called the class group of discriminant D. Gauss also considered a coarser notion of equivalence, under which the set of binary quadratic forms of a fixed discriminant splits into several genera of forms and each genus consists of finitely many classes of forms.
An integral binary quadratic form is called primitive if a, b, and c have no common factor. If a form's discriminant is a fundamental discriminant
, then the form is primitive.
From a modern perspective, the class group of a fundamental discriminant D is isomorphic to the narrow class group
of the quadratic field
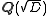of discriminant D. For negative D, the narrow class group is the same as the ideal class group
, but for positive D it may be twice as big.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, a binary quadratic form is a quadratic form
Quadratic form
In mathematics, a quadratic form is a homogeneous polynomial of degree two in a number of variables. For example,4x^2 + 2xy - 3y^2\,\!is a quadratic form in the variables x and y....
in two variables. More concretely, it is a homogeneous polynomial
Homogeneous polynomial
In mathematics, a homogeneous polynomial is a polynomial whose monomials with nonzero coefficients all have thesame total degree. For example, x^5 + 2 x^3 y^2 + 9 x y^4 is a homogeneous polynomial...
of degree 2 in two variables
where a, b, c are the coefficients. Properties of binary quadratic forms depend in an essential way on the nature of the coefficients, which may be real number
Real number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
s, rational number
Rational number
In mathematics, a rational number is any number that can be expressed as the quotient or fraction a/b of two integers, with the denominator b not equal to zero. Since b may be equal to 1, every integer is a rational number...
s, or in the most delicate case, integer
Integer
The integers are formed by the natural numbers together with the negatives of the non-zero natural numbers .They are known as Positive and Negative Integers respectively...
s. Arithmetical aspects of the theory of binary quadratic forms are related to the arithmetic of quadratic field
Quadratic field
In algebraic number theory, a quadratic field is an algebraic number field K of degree two over Q. It is easy to show that the map d ↦ Q is a bijection from the set of all square-free integers d ≠ 0, 1 to the set of all quadratic fields...
s and have been much studied, notably, by Gauss
Gauss
Gauss may refer to:*Carl Friedrich Gauss, German mathematician and physicist*Gauss , a unit of magnetic flux density or magnetic induction*GAUSS , a software package*Gauss , a crater on the moon...
in Section V of Disquisitiones Arithmeticae
Disquisitiones Arithmeticae
The Disquisitiones Arithmeticae is a textbook of number theory written in Latin by Carl Friedrich Gauss in 1798 when Gauss was 21 and first published in 1801 when he was 24...
. The theory of binary quadratic forms has been extended in two directions: general number fields and quadratic forms in n variables.
Brief history
Binary quadratic forms were considered already by Fermat, in particular, in the question of representations of numbers as sums of two squares. The theory of Pell's equationPell's equation
Pell's equation is any Diophantine equation of the formx^2-ny^2=1\,where n is a nonsquare integer. The word Diophantine means that integer values of x and y are sought. Trivially, x = 1 and y = 0 always solve this equation...
may be viewed as a part of the theory of binary quadratic forms. Lagrange
Lagrange
La Grange literally means the barn in French. Lagrange may refer to:- People :* Charles Varlet de La Grange , French actor* Georges Lagrange , translator to and writer in Esperanto...
in 1773 initiated the development of the general theory of quadratic forms. First systematic treatment of binary quadratic forms is due to Legendre
Adrien-Marie Legendre
Adrien-Marie Legendre was a French mathematician.The Moon crater Legendre is named after him.- Life :...
. Their theory was advanced much further by Gauss
Carl Friedrich Gauss
Johann Carl Friedrich Gauss was a German mathematician and scientist who contributed significantly to many fields, including number theory, statistics, analysis, differential geometry, geodesy, geophysics, electrostatics, astronomy and optics.Sometimes referred to as the Princeps mathematicorum...
in Disquisitiones Arithmeticae
Disquisitiones Arithmeticae
The Disquisitiones Arithmeticae is a textbook of number theory written in Latin by Carl Friedrich Gauss in 1798 when Gauss was 21 and first published in 1801 when he was 24...
. He considered questions of equivalence and reduction and introduced composition of binary quadratic forms (Gauss and many subsequent authors wrote 2b in place of b; the modern convention allowing the coefficient of xy to be odd is due to Eisenstein). These investigations of Gauss strongly influenced both the arithmetical theory of quadratic forms in more than two variables and the subsequent development of algebraic number theory, where quadratic fields are replaced with more general number fields.
Main questions
A classical question in the theory of integral quadratic forms is the representation problem: describe the set of numbers represented by a given quadratic form q. If the number of representations is finite then a further question is to give a closed formula for this number. The notion of equivalence of quadratic forms and the related reduction theory are the principal tools in addressing these questions.Two integral forms are called equivalent if there exists an invertible integral linear change of variables that transforms the first form into the second. This defines an equivalence relation
Equivalence relation
In mathematics, an equivalence relation is a relation that, loosely speaking, partitions a set so that every element of the set is a member of one and only one cell of the partition. Two elements of the set are considered equivalent if and only if they are elements of the same cell...
on the set of integral quadratic forms, whose elements are called classes of quadratic forms. Equivalent forms necessarily have the same discriminant
Gauss proved that for every value D, there are only finitely many classes of binary quadratic forms with discriminant D. Their number is the class number of discriminant D. He described an algorithm, called reduction, for constructing a canonical representative in each class, the reduced form, whose coefficients are the smallest in a suitable sense. One of the deepest discoveries of Gauss was the existence of a natural composition law on the set of classes of binary quadratic forms of given discriminant, which makes this set into a finite abelian group
Abelian group
In abstract algebra, an abelian group, also called a commutative group, is a group in which the result of applying the group operation to two group elements does not depend on their order . Abelian groups generalize the arithmetic of addition of integers...
called the class group of discriminant D. Gauss also considered a coarser notion of equivalence, under which the set of binary quadratic forms of a fixed discriminant splits into several genera of forms and each genus consists of finitely many classes of forms.
An integral binary quadratic form is called primitive if a, b, and c have no common factor. If a form's discriminant is a fundamental discriminant
Fundamental discriminant
In mathematics, a fundamental discriminant D is an integer invariant in the theory of integral binary quadratic forms. If is a quadratic form with integer coefficients, then is the discriminant of Q. Conversely, every integer D with is the discriminant of some binary quadratic form with integer...
, then the form is primitive.
From a modern perspective, the class group of a fundamental discriminant D is isomorphic to the narrow class group
Narrow class group
In algebraic number theory, the narrow class group of a number field K is a refinement of the class group of K that takes into account some information about embeddings of K into the field of real numbers.- Formal definition :...
of the quadratic field
Quadratic field
In algebraic number theory, a quadratic field is an algebraic number field K of degree two over Q. It is easy to show that the map d ↦ Q is a bijection from the set of all square-free integers d ≠ 0, 1 to the set of all quadratic fields...
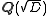of discriminant D. For negative D, the narrow class group is the same as the ideal class groupIdeal class group
In mathematics, the extent to which unique factorization fails in the ring of integers of an algebraic number field can be described by a certain group known as an ideal class group...
, but for positive D it may be twice as big.