
Fundamental discriminant
Encyclopedia
In mathematics
, a fundamental discriminant D is an integer
invariant
in the theory of integral
binary
quadratic form
s. If is a quadratic form with integer coefficients, then is the discriminant
of Q(x, y). Conversely, every integer D with is the discriminant of some binary quadratic form with integer coefficients. Thus, all such integers are referred to as discriminants in this theory. Every discriminant may be written as
with D0 a discriminant and f a positive integer. A discriminant D is called a fundamental discriminant if f = 1 in every such decomposition. Conversely, every discriminant D ≠ 0 can be written uniquely as D0f 2 where D0 is a fundamental discriminant. Thus, fundamental discriminants play a similar role for discriminants as prime number
s do for all integers.
There are explicit congruence
conditions that give the set of fundamental discriminants. Specifically, D is a fundamental discriminant if, and only if, one of the following statements holds
The first ten positive fundamental discriminants are:
The first ten negative fundamental discriminants are:
. A basic property of this connection is that D0 is a fundamental discriminant if, and only if, D0 = 1 or D0 is the discriminant
of a quadratic number field. There is exactly one quadratic field for every fundamental discriminant D0 ≠ 1, up to isomorphism
.
Caution: This is the reason why some authors consider 1 not to be a fundamental discriminant. One may interpret D0 = 1 as the degenerated "quadratic" field Q (the rational number
s).
. Define the set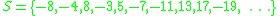
where the prime number
s ≡ 1 (mod 4) are positive and those ≡ 3 (mod 4) are negative. Then, a number D0 ≠ 1 is a fundamental discriminant if, and only if, it is the product of pairwise relatively prime
members of S.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, a fundamental discriminant D is an integer
Integer
The integers are formed by the natural numbers together with the negatives of the non-zero natural numbers .They are known as Positive and Negative Integers respectively...
invariant
Invariant (mathematics)
In mathematics, an invariant is a property of a class of mathematical objects that remains unchanged when transformations of a certain type are applied to the objects. The particular class of objects and type of transformations are usually indicated by the context in which the term is used...
in the theory of integral
Integer
The integers are formed by the natural numbers together with the negatives of the non-zero natural numbers .They are known as Positive and Negative Integers respectively...
binary
Binary function
In mathematics, a binary function, or function of two variables, is a function which takes two inputs.Precisely stated, a function f is binary if there exists sets X, Y, Z such that\,f \colon X \times Y \rightarrow Z...
quadratic form
Quadratic form
In mathematics, a quadratic form is a homogeneous polynomial of degree two in a number of variables. For example,4x^2 + 2xy - 3y^2\,\!is a quadratic form in the variables x and y....
s. If is a quadratic form with integer coefficients, then is the discriminant
Discriminant
In algebra, the discriminant of a polynomial is an expression which gives information about the nature of the polynomial's roots. For example, the discriminant of the quadratic polynomialax^2+bx+c\,is\Delta = \,b^2-4ac....
of Q(x, y). Conversely, every integer D with is the discriminant of some binary quadratic form with integer coefficients. Thus, all such integers are referred to as discriminants in this theory. Every discriminant may be written as
- D = D0f 2
with D0 a discriminant and f a positive integer. A discriminant D is called a fundamental discriminant if f = 1 in every such decomposition. Conversely, every discriminant D ≠ 0 can be written uniquely as D0f 2 where D0 is a fundamental discriminant. Thus, fundamental discriminants play a similar role for discriminants as prime number
Prime number
A prime number is a natural number greater than 1 that has no positive divisors other than 1 and itself. A natural number greater than 1 that is not a prime number is called a composite number. For example 5 is prime, as only 1 and 5 divide it, whereas 6 is composite, since it has the divisors 2...
s do for all integers.
There are explicit congruence
Modular arithmetic
In mathematics, modular arithmetic is a system of arithmetic for integers, where numbers "wrap around" after they reach a certain value—the modulus....
conditions that give the set of fundamental discriminants. Specifically, D is a fundamental discriminant if, and only if, one of the following statements holds
- D ≡ 1 (mod 4) and is square-freeSquare-free integerIn mathematics, a square-free, or quadratfrei, integer is one divisible by no perfect square, except 1. For example, 10 is square-free but 18 is not, as it is divisible by 9 = 32...
, - D = 4m, where m ≡ 2 or 3 (mod 4) and m is square-free.
The first ten positive fundamental discriminants are:
- 1, 5, 8, 1212 (number)12 is the natural number following 11 and preceding 13.The word "twelve" is the largest number with a single-morpheme name in English. Etymology suggests that "twelve" arises from the Germanic compound twalif "two-leftover", so a literal translation would yield "two remaining [after having ten...
, 1313 (number)13 is the natural number after 12 and before 14. It is the smallest number with eight letters in its name spelled out in English. It is also the first of the teens – the numbers 13 through 19 – the ages of teenagers....
, 1717 (number)17 is the natural number following 16 and preceding 18. It is prime.In spoken English, the numbers 17 and 70 are sometimes confused because they sound similar. When carefully enunciated, they differ in which syllable is stressed: 17 vs 70...
, 2121 (number)21 is the natural number following 20 and preceding 22.-In mathematics:Twenty-one is the fifth discrete Semiprime and the second in the family. With 22 it forms the second discrete Semiprime pair...
, 2424 (number)24 is the natural number following 23 and preceding 25.The SI prefix for 1024 is yotta , and for 10−24 yocto...
, 2828 (number)28 is the natural number following 27 and preceding 29.-In mathematics:It is a composite number, its proper divisors being 1, 2, 4, 7, and 14....
, 2929 (number)29 is the natural number following 28 and preceding 30.-In mathematics:It is the tenth prime number, and also the fourth primorial prime. It forms a twin prime pair with thirty-one, which is also a primorial prime. Twenty-nine is also the sixth Sophie Germain prime. It is also the sum of three...
, 3333 (number)33 is the natural number following 32 and preceding 34.-In mathematics:33 is the largest positive integer that cannot be expressed as a sum of different triangular numbers. It is also the smallest odd repdigit that is not a prime number.33 is the eighth distinct semiprime comprising the prime...
.
The first ten negative fundamental discriminants are:
- −3, −4, −7, −8, −11, −15, −19, −20, −23, −24, −31 .
Connection with quadratic fields
There is a connection between the theory of integral binary quadratic forms and the arithmetic of quadratic number fieldsQuadratic field
In algebraic number theory, a quadratic field is an algebraic number field K of degree two over Q. It is easy to show that the map d ↦ Q is a bijection from the set of all square-free integers d ≠ 0, 1 to the set of all quadratic fields...
. A basic property of this connection is that D0 is a fundamental discriminant if, and only if, D0 = 1 or D0 is the discriminant
Discriminant of an algebraic number field
In mathematics, the discriminant of an algebraic number field is a numerical invariant that, loosely speaking, measures the size of the algebraic number field...
of a quadratic number field. There is exactly one quadratic field for every fundamental discriminant D0 ≠ 1, up to isomorphism
Isomorphism
In abstract algebra, an isomorphism is a mapping between objects that shows a relationship between two properties or operations. If there exists an isomorphism between two structures, the two structures are said to be isomorphic. In a certain sense, isomorphic structures are...
.
Caution: This is the reason why some authors consider 1 not to be a fundamental discriminant. One may interpret D0 = 1 as the degenerated "quadratic" field Q (the rational number
Rational number
In mathematics, a rational number is any number that can be expressed as the quotient or fraction a/b of two integers, with the denominator b not equal to zero. Since b may be equal to 1, every integer is a rational number...
s).
Factorization
Fundamental discriminants may also be characterized by their factorization into positive and negative prime powersFundamental theorem of arithmetic
In number theory, the fundamental theorem of arithmetic states that any integer greater than 1 can be written as a unique product of prime numbers...
. Define the set
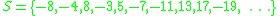
where the prime number
Prime number
A prime number is a natural number greater than 1 that has no positive divisors other than 1 and itself. A natural number greater than 1 that is not a prime number is called a composite number. For example 5 is prime, as only 1 and 5 divide it, whereas 6 is composite, since it has the divisors 2...
s ≡ 1 (mod 4) are positive and those ≡ 3 (mod 4) are negative. Then, a number D0 ≠ 1 is a fundamental discriminant if, and only if, it is the product of pairwise relatively prime
Greatest common divisor
In mathematics, the greatest common divisor , also known as the greatest common factor , or highest common factor , of two or more non-zero integers, is the largest positive integer that divides the numbers without a remainder.For example, the GCD of 8 and 12 is 4.This notion can be extended to...
members of S.

