Binary function
Encyclopedia
In mathematics
, a binary function, or function of two variables, is a function
which takes two inputs.
Precisely stated, a function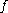
is binary if there exists sets 
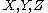such that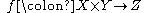
where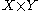
is the Cartesian product
of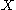
and 
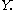
For example, if Z is the set of integer
s, N+ is the set of natural number
s (except for zero), and Q is the set of rational number
s, then division
is a binary function from Z and N+ to Q.
Set-theoretically
, one may represent a binary function as a subset
of the Cartesian product
X × Y × Z, where (x,y,z) belongs to the subset if and only if
f(x,y) = z.
Conversely, a subset R defines a binary function if and only if, for any x in X and y in Y, there exists a unique z in Z such that (x,y,z) belongs to R.
We then define f (x,y) to be this z.
Alternatively, a binary function may be interpreted as simply a function
from X × Y to Z.
Even when thought of this way, however, one generally writes f (x,y) instead of f((x,y)).
(That is, the same pair of parentheses is used to indicate both function application
and the formation of an ordered pair
.)
In turn, one can also derive ordinary functions of one variable from a binary function.
Given any element x of X, there is a function f x, or f (x,·), from Y to Z, given by f x(y) := f (x,y).
Similarly, given any element y of Y, there is a function f y, or f (·,y), from X to Z, given by f y(x) := f (x,y). (In computer science, this identification between a function from X × Y to Z and a function from X to ZY is called Currying
.)
The various concepts relating to functions can also be generalised to binary functions.
For example, the division example above is surjective
(or onto) because every rational number may be expressed as a quotient of an integer and a natural number.
This example is injective
in each input separately, because the functions f x and f y are always injective.
However, it's not injective in both variables simultaneously, because (for example) f (2,4) = f (1,2).
One can also consider partial binary functions, which may be defined only for certain values of the inputs.
For example, the division example above may also be interpreted as a partial binary function from Z and N to Q, where N is the set of all natural numbers, including zero.
But this function is undefined when the second input is zero.
A binary operation
is a binary function where the sets X, Y, and Z are all equal; binary operations are often used to define algebraic structure
s.
In linear algebra
, a bilinear transformation
is a binary function where the sets X, Y, and Z are all vector space
s and the derived functions f x and fy are all linear transformation
s.
A bilinear transformation, like any binary function, can be interpreted as a function from X × Y to Z, but this function in general won't be linear.
However, the bilinear transformation can also be interpreted as a single linear transformation from the tensor product
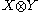to Z.
The concept of binary function generalises to ternary (or 3-ary) function, quaternary (or 4-ary) function, or more generally to n-ary function for any natural number
n.
A 0-ary function to Z is simply given by an element of Z.
One can also define an A-ary function where A is any set; there is one input for each element of A.
In category theory
, n-ary functions generalise to n-ary morphisms in a multicategory
.
The interpretation of an n-ary morphism as an ordinary morphisms whose domain is some sort of product of the domains of the original n-ary morphism will work in a monoidal category
.
The construction of the derived morphisms of one variable will work in a closed monoidal category
.
The category of sets is closed monoidal, but so is the category of vector spaces, giving the notion of bilinear transformation above.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, a binary function, or function of two variables, is a function
Function (mathematics)
In mathematics, a function associates one quantity, the argument of the function, also known as the input, with another quantity, the value of the function, also known as the output. A function assigns exactly one output to each input. The argument and the value may be real numbers, but they can...
which takes two inputs.
Precisely stated, a function
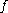is binary if there exists sets 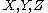such that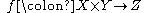where
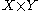is the Cartesian productCartesian product
In mathematics, a Cartesian product is a construction to build a new set out of a number of given sets. Each member of the Cartesian product corresponds to the selection of one element each in every one of those sets...
of
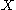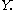
and For example, if Z is the set of integer
Integer
The integers are formed by the natural numbers together with the negatives of the non-zero natural numbers .They are known as Positive and Negative Integers respectively...
s, N+ is the set of natural number
Natural number
In mathematics, the natural numbers are the ordinary whole numbers used for counting and ordering . These purposes are related to the linguistic notions of cardinal and ordinal numbers, respectively...
s (except for zero), and Q is the set of rational number
Rational number
In mathematics, a rational number is any number that can be expressed as the quotient or fraction a/b of two integers, with the denominator b not equal to zero. Since b may be equal to 1, every integer is a rational number...
s, then division
Division (mathematics)
right|thumb|200px|20 \div 4=5In mathematics, especially in elementary arithmetic, division is an arithmetic operation.Specifically, if c times b equals a, written:c \times b = a\,...
is a binary function from Z and N+ to Q.
Set-theoretically
Naive set theory
Naive set theory is one of several theories of sets used in the discussion of the foundations of mathematics. The informal content of this naive set theory supports both the aspects of mathematical sets familiar in discrete mathematics , and the everyday usage of set theory concepts in most...
, one may represent a binary function as a subset
Subset
In mathematics, especially in set theory, a set A is a subset of a set B if A is "contained" inside B. A and B may coincide. The relationship of one set being a subset of another is called inclusion or sometimes containment...
of the Cartesian product
Cartesian product
In mathematics, a Cartesian product is a construction to build a new set out of a number of given sets. Each member of the Cartesian product corresponds to the selection of one element each in every one of those sets...
X × Y × Z, where (x,y,z) belongs to the subset if and only if
If and only if
In logic and related fields such as mathematics and philosophy, if and only if is a biconditional logical connective between statements....
f(x,y) = z.
Conversely, a subset R defines a binary function if and only if, for any x in X and y in Y, there exists a unique z in Z such that (x,y,z) belongs to R.
We then define f (x,y) to be this z.
Alternatively, a binary function may be interpreted as simply a function
Function (mathematics)
In mathematics, a function associates one quantity, the argument of the function, also known as the input, with another quantity, the value of the function, also known as the output. A function assigns exactly one output to each input. The argument and the value may be real numbers, but they can...
from X × Y to Z.
Even when thought of this way, however, one generally writes f (x,y) instead of f((x,y)).
(That is, the same pair of parentheses is used to indicate both function application
Function application
In mathematics, function application is the act of applying a function to an argument from its domain so as to obtain the corresponding value from its range.-Representation:...
and the formation of an ordered pair
Ordered pair
In mathematics, an ordered pair is a pair of mathematical objects. In the ordered pair , the object a is called the first entry, and the object b the second entry of the pair...
.)
In turn, one can also derive ordinary functions of one variable from a binary function.
Given any element x of X, there is a function f x, or f (x,·), from Y to Z, given by f x(y) := f (x,y).
Similarly, given any element y of Y, there is a function f y, or f (·,y), from X to Z, given by f y(x) := f (x,y). (In computer science, this identification between a function from X × Y to Z and a function from X to ZY is called Currying
Currying
In mathematics and computer science, currying is the technique of transforming a function that takes multiple arguments in such a way that it can be called as a chain of functions each with a single argument...
.)
The various concepts relating to functions can also be generalised to binary functions.
For example, the division example above is surjective
Surjective function
In mathematics, a function f from a set X to a set Y is surjective , or a surjection, if every element y in Y has a corresponding element x in X so that f = y...
(or onto) because every rational number may be expressed as a quotient of an integer and a natural number.
This example is injective
Injective function
In mathematics, an injective function is a function that preserves distinctness: it never maps distinct elements of its domain to the same element of its codomain. In other words, every element of the function's codomain is mapped to by at most one element of its domain...
in each input separately, because the functions f x and f y are always injective.
However, it's not injective in both variables simultaneously, because (for example) f (2,4) = f (1,2).
One can also consider partial binary functions, which may be defined only for certain values of the inputs.
For example, the division example above may also be interpreted as a partial binary function from Z and N to Q, where N is the set of all natural numbers, including zero.
But this function is undefined when the second input is zero.
A binary operation
Binary operation
In mathematics, a binary operation is a calculation involving two operands, in other words, an operation whose arity is two. Examples include the familiar arithmetic operations of addition, subtraction, multiplication and division....
is a binary function where the sets X, Y, and Z are all equal; binary operations are often used to define algebraic structure
Algebraic structure
In abstract algebra, an algebraic structure consists of one or more sets, called underlying sets or carriers or sorts, closed under one or more operations, satisfying some axioms. Abstract algebra is primarily the study of algebraic structures and their properties...
s.
In linear algebra
Linear algebra
Linear algebra is a branch of mathematics that studies vector spaces, also called linear spaces, along with linear functions that input one vector and output another. Such functions are called linear maps and can be represented by matrices if a basis is given. Thus matrix theory is often...
, a bilinear transformation
Bilinear operator
In mathematics, a bilinear operator is a function combining elements of two vector spaces to yield an element of a third vector space that is linear in each of its arguments. Matrix multiplication is an example.-Definition:...
is a binary function where the sets X, Y, and Z are all vector space
Vector space
A vector space is a mathematical structure formed by a collection of vectors: objects that may be added together and multiplied by numbers, called scalars in this context. Scalars are often taken to be real numbers, but one may also consider vector spaces with scalar multiplication by complex...
s and the derived functions f x and fy are all linear transformation
Linear transformation
In mathematics, a linear map, linear mapping, linear transformation, or linear operator is a function between two vector spaces that preserves the operations of vector addition and scalar multiplication. As a result, it always maps straight lines to straight lines or 0...
s.
A bilinear transformation, like any binary function, can be interpreted as a function from X × Y to Z, but this function in general won't be linear.
However, the bilinear transformation can also be interpreted as a single linear transformation from the tensor product
Tensor product
In mathematics, the tensor product, denoted by ⊗, may be applied in different contexts to vectors, matrices, tensors, vector spaces, algebras, topological vector spaces, and modules, among many other structures or objects. In each case the significance of the symbol is the same: the most general...
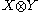to Z.The concept of binary function generalises to ternary (or 3-ary) function, quaternary (or 4-ary) function, or more generally to n-ary function for any natural number
Natural number
In mathematics, the natural numbers are the ordinary whole numbers used for counting and ordering . These purposes are related to the linguistic notions of cardinal and ordinal numbers, respectively...
n.
A 0-ary function to Z is simply given by an element of Z.
One can also define an A-ary function where A is any set; there is one input for each element of A.
In category theory
Category theory
Category theory is an area of study in mathematics that examines in an abstract way the properties of particular mathematical concepts, by formalising them as collections of objects and arrows , where these collections satisfy certain basic conditions...
, n-ary functions generalise to n-ary morphisms in a multicategory
Multicategory
In mathematics , a multicategory is a generalization of the concept of category that allows morphisms of multiple arity...
.
The interpretation of an n-ary morphism as an ordinary morphisms whose domain is some sort of product of the domains of the original n-ary morphism will work in a monoidal category
Monoidal category
In mathematics, a monoidal category is a category C equipped with a bifunctorwhich is associative, up to a natural isomorphism, and an object I which is both a left and right identity for ⊗, again up to a natural isomorphism...
.
The construction of the derived morphisms of one variable will work in a closed monoidal category
Closed monoidal category
In mathematics, especially in category theory, aclosed monoidal category is a context where we can take tensor products of objects and also form 'mapping objects'. A classic example is the category of sets, Set, where the tensor product of sets A and B is the usual cartesian product A \times B, and...
.
The category of sets is closed monoidal, but so is the category of vector spaces, giving the notion of bilinear transformation above.