Closed monoidal category
Encyclopedia
In mathematics
, especially in category theory
, a
closed monoidal category is a context where we can take tensor products of objects and also form 'mapping objects'. A classic example is the category of sets
, Set, where the tensor product of sets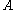
and 
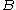is the usual cartesian product
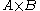, and the mapping object 
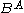is the set of function
s from
to 
. Another example is the category FdVect, consisting of finite-dimensional vector space
s and linear maps. Here the tensor product is the usual tensor product
of vector spaces, and the mapping object is the vector space of linear maps from one vector space to another.
Technically, what we have been calling a 'mapping object' is called the 'internal Hom'.
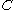such that for every object 
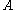the functor
given by left tensoring with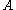
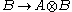
has a right adjoint, written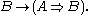
This means that there exists a bijection between the Hom-sets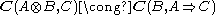
that is natural in both B and C.
Equivalently, a closed monoidal category C is a category equipped, for every two objects A and B, with
satisfying the following universal property: for every morphism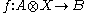
there exists a unique morphism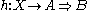
such that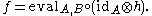
It can be shown that this construction defines a functor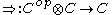
. This functor is called the internal Hom functor, and the object 
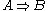is called the internal Hom of 
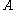and 
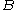. Many other notations are in common use for the internal Hom. When the tensor product on C is the cartesian product, the usual notation is 
.
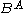Strictly speaking, we have defined a left closed monoidal category, since we required that left tensoring with any object
has a right adjoint. In a right closed monoidal category, we instead demand that the functor of right tensoring with any object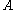 
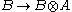
have a right adjoint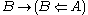
(Beware: almost all authors use the opposite terminology.)
A biclosed monoidal category is a monoidal category that is both left and right closed.
A symmetric monoidal category is left closed if and only if it is right closed. Thus we may safely speak of a 'symmetric monoidal closed category' without specifying whether it is left or right closed. In fact, the same is true more generally for braided monoidal categories: since the braiding makes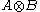
naturally isomorphic to 
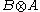, the distinction between tensoring on the left and tensoring on the right becomes immaterial, so every right closed braided monoidal category becomes left closed in a canonical way, and vice versa.
We have described closed monoidal categories as monoidal categories with an extra property. One can equivalently defined a closed monoidal category to be a closed category
with an extra property. Namely, we can demand the existence of a tensor product
that is left adjoint to the internal Hom functor.
In this approach, closed monoidal categories are also called monoidal closed categories.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, especially in category theory
Category theory
Category theory is an area of study in mathematics that examines in an abstract way the properties of particular mathematical concepts, by formalising them as collections of objects and arrows , where these collections satisfy certain basic conditions...
, a
closed monoidal category is a context where we can take tensor products of objects and also form 'mapping objects'. A classic example is the category of sets
Category of sets
In the mathematical field of category theory, the category of sets, denoted as Set, is the category whose objects are sets. The arrows or morphisms between sets A and B are all functions from A to B...
, Set, where the tensor product of sets
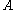and 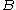is the usual cartesian productCartesian product
In mathematics, a Cartesian product is a construction to build a new set out of a number of given sets. Each member of the Cartesian product corresponds to the selection of one element each in every one of those sets...
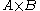, and the mapping object 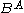is the set of functionFunction (mathematics)
In mathematics, a function associates one quantity, the argument of the function, also known as the input, with another quantity, the value of the function, also known as the output. A function assigns exactly one output to each input. The argument and the value may be real numbers, but they can...
s from
to . Another example is the category FdVect, consisting of finite-dimensional vector spaceVector space
A vector space is a mathematical structure formed by a collection of vectors: objects that may be added together and multiplied by numbers, called scalars in this context. Scalars are often taken to be real numbers, but one may also consider vector spaces with scalar multiplication by complex...
s and linear maps. Here the tensor product is the usual tensor product
Tensor product
In mathematics, the tensor product, denoted by ⊗, may be applied in different contexts to vectors, matrices, tensors, vector spaces, algebras, topological vector spaces, and modules, among many other structures or objects. In each case the significance of the symbol is the same: the most general...
of vector spaces, and the mapping object is the vector space of linear maps from one vector space to another.
Technically, what we have been calling a 'mapping object' is called the 'internal Hom'.
Definition
A closed monoidal category is a monoidal categoryMonoidal category
In mathematics, a monoidal category is a category C equipped with a bifunctorwhich is associative, up to a natural isomorphism, and an object I which is both a left and right identity for ⊗, again up to a natural isomorphism...
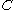such that for every object 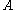the functorFunctor
In category theory, a branch of mathematics, a functor is a special type of mapping between categories. Functors can be thought of as homomorphisms between categories, or morphisms when in the category of small categories....
given by left tensoring with
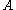
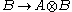
has a right adjoint, written
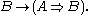
This means that there exists a bijection between the Hom-sets
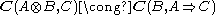
that is natural in both B and C.
Equivalently, a closed monoidal category C is a category equipped, for every two objects A and B, with
- an object
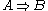, - a morphism
,
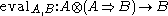satisfying the following universal property: for every morphism
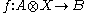
there exists a unique morphism
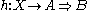
such that
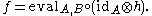
It can be shown that this construction defines a functor
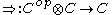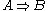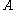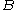. This functor is called the internal Hom functor, and the object is called the internal Hom of and . Many other notations are in common use for the internal Hom. When the tensor product on C is the cartesian product, the usual notation is 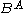.Strictly speaking, we have defined a left closed monoidal category, since we required that left tensoring with any object
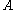
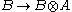
has a right adjoint. In a right closed monoidal category, we instead demand that the functor of right tensoring with any object have a right adjoint
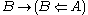
(Beware: almost all authors use the opposite terminology.)
A biclosed monoidal category is a monoidal category that is both left and right closed.
A symmetric monoidal category is left closed if and only if it is right closed. Thus we may safely speak of a 'symmetric monoidal closed category' without specifying whether it is left or right closed. In fact, the same is true more generally for braided monoidal categories: since the braiding makes
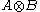naturally isomorphic to 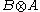, the distinction between tensoring on the left and tensoring on the right becomes immaterial, so every right closed braided monoidal category becomes left closed in a canonical way, and vice versa.We have described closed monoidal categories as monoidal categories with an extra property. One can equivalently defined a closed monoidal category to be a closed category
Closed category
In category theory, a branch of mathematics, a closed category is a special kind of category.In any category , the morphisms between any two given objects x and y comprise a set, the external hom...
with an extra property. Namely, we can demand the existence of a tensor product
Monoidal category
In mathematics, a monoidal category is a category C equipped with a bifunctorwhich is associative, up to a natural isomorphism, and an object I which is both a left and right identity for ⊗, again up to a natural isomorphism...
that is left adjoint to the internal Hom functor.
In this approach, closed monoidal categories are also called monoidal closed categories.
Examples
- The monoidal category Set of sets and functions, with cartesian product as the tensor product, is a closed monoidal category. Here
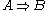is the set of functions from 
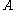to 
. This example is a cartesian closed categoryCartesian closed categoryIn category theory, a category is cartesian closed if, roughly speaking, any morphism defined on a product of two objects can be naturally identified with a morphism defined on one of the factors. These categories are particularly important in mathematical logic and the theory of programming, in...
. - More generally, every cartesian closed categoryCartesian closed categoryIn category theory, a category is cartesian closed if, roughly speaking, any morphism defined on a product of two objects can be naturally identified with a morphism defined on one of the factors. These categories are particularly important in mathematical logic and the theory of programming, in...
is a symmetric monoidal closed category, when the monoidal structure is the cartesian product structure. Here the internal hom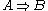
is usually written 
. - The monoidal category FdVect of finite-dimensional vector spaces and linear maps, with its usual tensor product, is a closed monoidal category. Here
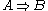is the vector space of linear maps from 
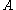to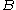 
. This example is a compact closed categoryCompact closed categoryIn category theory, compact closed categories are a general context for treating dual objects. The idea of a dual object generalizes the more familiar concept of the dual of a finite-dimensional vector space...
. - More generally, every compact closed categoryCompact closed categoryIn category theory, compact closed categories are a general context for treating dual objects. The idea of a dual object generalizes the more familiar concept of the dual of a finite-dimensional vector space...
is a symmetric monoidal closed category, in which the internal Hom functor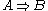
is given by 
.