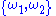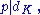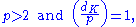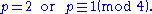Narrow class group
Encyclopedia
In algebraic number theory
, the narrow class group of a number field K is a refinement of the class group of K that takes into account some information about embeddings of K into the field of real number
s.

where IK is the group of fractional ideal
s of K, and PK is the group of principal fractional ideals of K, that is, ideals of the form aOK where a is a unit
of K.
The narrow class group is defined to be the quotient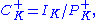
where now PK+ is the group of totally positive principal fractional ideals of K; that is, ideals of the form aOK where a is a unit of K such that σ(a) is positive for every embedding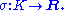
s. An example is the following result (Fröhlich and Taylor, Chapter V, Theorem 1.25).
Algebraic number theory
Algebraic number theory is a major branch of number theory which studies algebraic structures related to algebraic integers. This is generally accomplished by considering a ring of algebraic integers O in an algebraic number field K/Q, and studying their algebraic properties such as factorization,...
, the narrow class group of a number field K is a refinement of the class group of K that takes into account some information about embeddings of K into the field of real number
Real number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
s.
Formal definition
Suppose that K is a finite extension of Q. Recall that the ordinary class group of K is defined to be
where IK is the group of fractional ideal
Fractional ideal
In mathematics, in particular commutative algebra, the concept of fractional ideal is introduced in the context of integral domains and is particularly fruitful in the study of Dedekind domains. In some sense, fractional ideals of an integral domain are like ideals where denominators are allowed...
s of K, and PK is the group of principal fractional ideals of K, that is, ideals of the form aOK where a is a unit
Unit (ring theory)
In mathematics, an invertible element or a unit in a ring R refers to any element u that has an inverse element in the multiplicative monoid of R, i.e. such element v that...
of K.
The narrow class group is defined to be the quotient
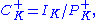
where now PK+ is the group of totally positive principal fractional ideals of K; that is, ideals of the form aOK where a is a unit of K such that σ(a) is positive for every embedding
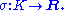
Uses
The narrow class group features prominently in the theory of representing of integers by quadratic formQuadratic form
In mathematics, a quadratic form is a homogeneous polynomial of degree two in a number of variables. For example,4x^2 + 2xy - 3y^2\,\!is a quadratic form in the variables x and y....
s. An example is the following result (Fröhlich and Taylor, Chapter V, Theorem 1.25).
- Theorem. Suppose that
- where d is a square-free integerSquare-free integerIn mathematics, a square-free, or quadratfrei, integer is one divisible by no perfect square, except 1. For example, 10 is square-free but 18 is not, as it is divisible by 9 = 32...
, and that the narrow class group of K is trivial. Suppose that - is a basis for the ring of integers of K. Define a quadratic form
-
 ,
,
-
- where NK/Q is the normField normIn mathematics, the norm is a mapping defined in field theory, to map elements of a larger field into a smaller one.-Formal definitions:1. Let K be a field and L a finite extension of K...
. Then a prime numberPrime numberA prime number is a natural number greater than 1 that has no positive divisors other than 1 and itself. A natural number greater than 1 that is not a prime number is called a composite number. For example 5 is prime, as only 1 and 5 divide it, whereas 6 is composite, since it has the divisors 2...
p is of the form -
- for some integers x and y if and only if either
-
- or
-
- or
- where dK is the discriminant of K, and
- indicates the Legendre symbolLegendre symbolIn number theory, the Legendre symbol is a multiplicative function with values 1, −1, 0 that is a quadratic character modulo a prime number p: its value on a quadratic residue mod p is 1 and on a quadratic non-residue is −1....
.
Examples
For example, one can prove that the quadratic fields Q(√−1), Q(√2), Q(√−3) all have trivial narrow class group. Then, by choosing appropriate bases for the integers of each of these fields, the above theorem implies the following:- A prime p is of the form p = x2 + y2 for integers x and y if and only if
-
- (This is known as Fermat's theorem on sums of two squares.)
- A prime p is of the form p = x2 − 2y2 for integers x and y if and only if
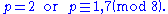
- A prime p is of the form p = x2 − xy + y2 for integers x and y if and only if
 (cf. Eisenstein primeEisenstein primeIn mathematics, an Eisenstein prime is an Eisenstein integerz = a + b\,\omega\qquadthat is irreducible in the ring-theoretic sense: its only Eisenstein divisors are the units , a + bω itself and its associates.The associates and the complex conjugate...
(cf. Eisenstein primeEisenstein primeIn mathematics, an Eisenstein prime is an Eisenstein integerz = a + b\,\omega\qquadthat is irreducible in the ring-theoretic sense: its only Eisenstein divisors are the units , a + bω itself and its associates.The associates and the complex conjugate...
)