Ideal number
Encyclopedia
In number theory
an ideal number is an algebraic integer
which represents an ideal in the ring
of integers of a number field; the idea was developed by Ernst Kummer
, and led to Richard Dedekind
's definition of ideal
s for rings. An ideal in the ring of integers of an algebraic number field is principal if it consists of multiples of a single element of the ring, and nonprincipal otherwise. By the principal ideal theorem
any nonprincipal ideal becomes principal when extended to an ideal of the Hilbert class field
. This means there is an element of the ring of integers of the class field, which is an ideal number, such that all multiples times elements of this ring of integers
lying in the ring of integers of the original field define the nonprincipal ideal.
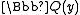is 
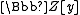, which means all a + by with a and b integers form the ring of integers. An example of a nonprincipal ideal in this ring is 2a + yb with a and b integers; the cube of this ideal is principal, and in fact the class group is cyclic of order three. The corresponding class field is obtained by adjoining an element w satisfying w3 − w − 1 = 0 to 
, giving 
. An ideal number for the nonprincipal ideal 2a + yb is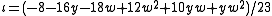 
. Since this satisfies the equation
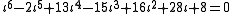it is an algebraic integer.
All elements of the ring of integers of the class field which when multiplied by ι give a result in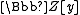
are of the form aα + bβ, where
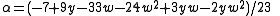
and
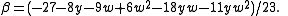
The coefficients α and β are also algebraic integers, satisfying
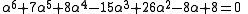
and
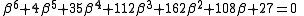
respectively. Multiplying aα + bβ by the ideal number ι gives 2a + by, which is the nonprincipal ideal.
journal. In subsequent papers in 1846 and 1847 he published his main theorem, the unique factorization into (actual and ideal) primes.
It is widely believed that Kummer was led to his "ideal complex numbers" by his interest in Fermat's Last Theorem
; there is even a story often told that Kummer, like Lamé
, believed he had proven Fermat's Last Theorem until Dirichlet
told him his argument relied on unique factorization; but the story was first told by Kurt Hensel
in 1910 and the evidence indicates it likely derives from a confusion by one of Hensel's sources. Harold Edwards
says the belief that Kummer was mainly interested in Fermat's Last Theorem "is surely mistaken" (op cit p. 79). Kummer's use of the letter λ to represent a prime number, α to denote a λth root of unity, and his study of the factorization of prime number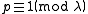
into "complex numbers composed of 
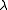th roots of unity" all derive directly from a paper of Jacobi
which is concerned with higher reciprocity laws. Kummer's 1844 memoir was in honor of the jubilee celebration of the University of Königsberg and was meant as a tribute to Jacobi. Although Kummer had studied Fermat's Last Theorem in the 1830s and was probably aware that his theory would have implications for its study, it is more likely that the subject of Jacobi's (and Gauss's
) interest, higher reciprocity laws, held more importance for him. Kummer referred to his own partial proof of Fermat's Last Theorem for regular primes as "a curiosity of number theory rather than a major item" and to the higher reciprocity law (which he stated as a conjecture) as "the principal subject and the pinnacle of contemporary number theory." On the other hand, this latter pronouncement was made when Kummer was still excited about the success of his work on reciprocity and when his work on Fermat's Last Theorem was running out of steam, so it may perhaps be taken with some skepticism.
The extension of Kummer's ideas to the general case was accomplished independently by Kronecker and Dedekind during the next forty years. A direct generalization encountered formidable difficulties, and it eventually led Dedekind to the creation of the theory of modules
and ideals
. Kronecker dealt with the difficulties by developing a theory of forms (a generalization of quadratic forms) and a theory of divisors
. Dedekind's contribution would become the basis of ring theory
and abstract algebra
, while Kronecker's would become major tools in algebraic geometry
.
Number theory
Number theory is a branch of pure mathematics devoted primarily to the study of the integers. Number theorists study prime numbers as well...
an ideal number is an algebraic integer
Algebraic integer
In number theory, an algebraic integer is a complex number that is a root of some monic polynomial with coefficients in . The set of all algebraic integers is closed under addition and multiplication and therefore is a subring of complex numbers denoted by A...
which represents an ideal in the ring
Ring (mathematics)
In mathematics, a ring is an algebraic structure consisting of a set together with two binary operations usually called addition and multiplication, where the set is an abelian group under addition and a semigroup under multiplication such that multiplication distributes over addition...
of integers of a number field; the idea was developed by Ernst Kummer
Ernst Kummer
Ernst Eduard Kummer was a German mathematician. Skilled in applied mathematics, Kummer trained German army officers in ballistics; afterwards, he taught for 10 years in a gymnasium, the German equivalent of high school, where he inspired the mathematical career of Leopold Kronecker.-Life:Kummer...
, and led to Richard Dedekind
Richard Dedekind
Julius Wilhelm Richard Dedekind was a German mathematician who did important work in abstract algebra , algebraic number theory and the foundations of the real numbers.-Life:...
's definition of ideal
Ideal (ring theory)
In ring theory, a branch of abstract algebra, an ideal is a special subset of a ring. The ideal concept allows the generalization in an appropriate way of some important properties of integers like "even number" or "multiple of 3"....
s for rings. An ideal in the ring of integers of an algebraic number field is principal if it consists of multiples of a single element of the ring, and nonprincipal otherwise. By the principal ideal theorem
Principal ideal theorem
In mathematics, the principal ideal theorem of class field theory, a branch of algebraic number theory, is the statement that for any algebraic number field K and any ideal I of the ring of integers of K, if L is the Hilbert class field of K, thenIO_L\ is a principal ideal αOL, for OL the ring of...
any nonprincipal ideal becomes principal when extended to an ideal of the Hilbert class field
Hilbert class field
In algebraic number theory, the Hilbert class field E of a number field K is the maximal abelian unramified extension of K. Its degree over K equals the class number of K and the Galois group of E over K is canonically isomorphic to the ideal class group of K using Frobenius elements for prime...
. This means there is an element of the ring of integers of the class field, which is an ideal number, such that all multiples times elements of this ring of integers
Algebraic number
In mathematics, an algebraic number is a number that is a root of a non-zero polynomial in one variable with rational coefficients. Numbers such as π that are not algebraic are said to be transcendental; almost all real numbers are transcendental...
lying in the ring of integers of the original field define the nonprincipal ideal.
Example
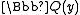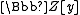For instance, let y be a root of y2 + y + 6 = 0, then the ring of integers of the field is , which means all a + by with a and b integers form the ring of integers. An example of a nonprincipal ideal in this ring is 2a + yb with a and b integers; the cube of this ideal is principal, and in fact the class group is cyclic of order three. The corresponding class field is obtained by adjoining an element w satisfying w3 − w − 1 = 0 to , giving . An ideal number for the nonprincipal ideal 2a + yb is 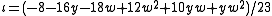. Since this satisfies the equation 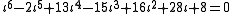it is an algebraic integer.All elements of the ring of integers of the class field which when multiplied by ι give a result in
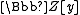are of the form aα + bβ, where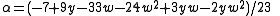and
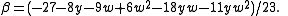
The coefficients α and β are also algebraic integers, satisfying
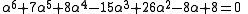
and
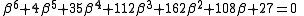
respectively. Multiplying aα + bβ by the ideal number ι gives 2a + by, which is the nonprincipal ideal.
History
Kummer first published the failure of unique factorization in cyclotomic fields in 1844 in an obscure journal; it was reprinted in 1847 in Liouville'sJoseph Liouville
- Life and work :Liouville graduated from the École Polytechnique in 1827. After some years as an assistant at various institutions including the Ecole Centrale Paris, he was appointed as professor at the École Polytechnique in 1838...
journal. In subsequent papers in 1846 and 1847 he published his main theorem, the unique factorization into (actual and ideal) primes.
It is widely believed that Kummer was led to his "ideal complex numbers" by his interest in Fermat's Last Theorem
Fermat's Last Theorem
In number theory, Fermat's Last Theorem states that no three positive integers a, b, and c can satisfy the equation an + bn = cn for any integer value of n greater than two....
; there is even a story often told that Kummer, like Lamé
Gabriel Lamé
Gabriel Léon Jean Baptiste Lamé was a French mathematician.-Biography:Lamé was born in Tours, in today's département of Indre-et-Loire....
, believed he had proven Fermat's Last Theorem until Dirichlet
Johann Peter Gustav Lejeune Dirichlet
Johann Peter Gustav Lejeune Dirichlet was a German mathematician with deep contributions to number theory , as well as to the theory of Fourier series and other topics in mathematical analysis; he is credited with being one of the first mathematicians to give the modern formal definition of a...
told him his argument relied on unique factorization; but the story was first told by Kurt Hensel
Kurt Hensel
Kurt Wilhelm Sebastian Hensel was a German mathematician born in Königsberg, Prussia.He was the son of the landowner and entrepreneur Sebastian Hensel, brother of the philosopher Paul Hensel, grandson of the composer Fanny Mendelssohn and the painter Wilhelm Hensel, and a descendant of the...
in 1910 and the evidence indicates it likely derives from a confusion by one of Hensel's sources. Harold Edwards
Harold Edwards (mathematician)
Harold Mortimer Edwards, Jr. is an American mathematician working in number theory, algebra, and the history and philosophy of mathematics....
says the belief that Kummer was mainly interested in Fermat's Last Theorem "is surely mistaken" (op cit p. 79). Kummer's use of the letter λ to represent a prime number, α to denote a λth root of unity, and his study of the factorization of prime number
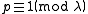into "complex numbers composed of 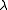th roots of unity" all derive directly from a paper of JacobiCarl Gustav Jakob Jacobi
Carl Gustav Jacob Jacobi was a German mathematician, widely considered to be the most inspiring teacher of his time and is considered one of the greatest mathematicians of his generation.-Biography:...
which is concerned with higher reciprocity laws. Kummer's 1844 memoir was in honor of the jubilee celebration of the University of Königsberg and was meant as a tribute to Jacobi. Although Kummer had studied Fermat's Last Theorem in the 1830s and was probably aware that his theory would have implications for its study, it is more likely that the subject of Jacobi's (and Gauss's
Carl Friedrich Gauss
Johann Carl Friedrich Gauss was a German mathematician and scientist who contributed significantly to many fields, including number theory, statistics, analysis, differential geometry, geodesy, geophysics, electrostatics, astronomy and optics.Sometimes referred to as the Princeps mathematicorum...
) interest, higher reciprocity laws, held more importance for him. Kummer referred to his own partial proof of Fermat's Last Theorem for regular primes as "a curiosity of number theory rather than a major item" and to the higher reciprocity law (which he stated as a conjecture) as "the principal subject and the pinnacle of contemporary number theory." On the other hand, this latter pronouncement was made when Kummer was still excited about the success of his work on reciprocity and when his work on Fermat's Last Theorem was running out of steam, so it may perhaps be taken with some skepticism.
The extension of Kummer's ideas to the general case was accomplished independently by Kronecker and Dedekind during the next forty years. A direct generalization encountered formidable difficulties, and it eventually led Dedekind to the creation of the theory of modules
Module (mathematics)
In abstract algebra, the concept of a module over a ring is a generalization of the notion of vector space, wherein the corresponding scalars are allowed to lie in an arbitrary ring...
and ideals
Ideal (ring theory)
In ring theory, a branch of abstract algebra, an ideal is a special subset of a ring. The ideal concept allows the generalization in an appropriate way of some important properties of integers like "even number" or "multiple of 3"....
. Kronecker dealt with the difficulties by developing a theory of forms (a generalization of quadratic forms) and a theory of divisors
Divisor (algebraic geometry)
In algebraic geometry, divisors are a generalization of codimension one subvarieties of algebraic varieties; two different generalizations are in common use, Cartier divisors and Weil divisors...
. Dedekind's contribution would become the basis of ring theory
Ring theory
In abstract algebra, ring theory is the study of rings—algebraic structures in which addition and multiplication are defined and have similar properties to those familiar from the integers...
and abstract algebra
Abstract algebra
Abstract algebra is the subject area of mathematics that studies algebraic structures, such as groups, rings, fields, modules, vector spaces, and algebras...
, while Kronecker's would become major tools in algebraic geometry
Algebraic geometry
Algebraic geometry is a branch of mathematics which combines techniques of abstract algebra, especially commutative algebra, with the language and the problems of geometry. It occupies a central place in modern mathematics and has multiple conceptual connections with such diverse fields as complex...
.
External links
- Ideal Numbers, Proof that the theory of ideal numbers saves unique factorization for cyclotomic integers at Fermat's Last Theorem Blog.