
Johann Peter Gustav Lejeune Dirichlet
Encyclopedia
Johann Peter Gustav Lejeune Dirichlet (ləˈʒœn diʁiˈkleː; 13 February 1805 – 5 May 1859) was a German
mathematician
with deep contributions to number theory
(including creating the field of analytic number theory
), as well as to the theory of Fourier series
and other topics in mathematical analysis
; he is credited with being one of the first mathematicians to give the modern formal definition of a function
.
, a town on the left bank of the Rhine which at the time was part of the First French Empire
, reverting to Prussia
after the Congress of Vienna
in 1815. His father Johann Arnold Lejeune Dirichlet was the postmaster, merchant, and city councilor. His paternal grandfather had come to Düren from Richelette, a small community 5 km north east of Liège
in Belgium
, from which his surname "Lejeune Dirichlet" ("", French
for "the youth from Richelette") was derived.
Although his family was not wealthy and he was the youngest of seven children, his parents supported his education. They enrolled him in an elementary school and then private school in hope that he would later become a merchant. The young Dirichlet, who showed a strong interest in mathematics before age 12, convinced his parents to allow him to continue his studies. In 1817 they sent him to the Gymnasium in Bonn under the care of Peter Joseph Elvenich
, a student his family knew. In 1820 Dirichlet moved to the Jesuit Gymnasium
in Cologne
, where his lessons with Georg Ohm
helped widen his knowledge in mathematics. He left the gymnasium a year later with only a certificate, as his inability to speak fluent Latin prevented him from earning the Abitur
.
at the University of Göttingen who was nominally a professor of astronomy and anyway disliked teaching, Dirichlet decided to go to Paris
in May 1822. There he attended classes at the Collège de France
and at the Faculté des sciences de Paris, learning mathematics from Hachette
among others, while undertaking private study of Gauss' Disquisitiones Arithmeticae
, a book he kept close for his entire life. In 1823 he was recommended to General Foy
, who hired him as a private tutor to teach his children German, the wage finally allowing Dirichlet to become independent from his parents' financial support.
His first original research, comprising part of a proof of Fermat's last theorem
for the case , brought him immediate fame, being the first advance in the theorem since Fermat
, brought him immediate fame, being the first advance in the theorem since Fermat
's own proof of the case and Euler
and Euler
's proof for . Adrien-Marie Legendre
. Adrien-Marie Legendre
, one of the referees, soon completed the proof for this case; Dirichlet completed his own proof a short time after Legendre, and a few years later produced a full proof for the case . In June 1825 he was accepted to lecture on his partial proof for the case
. In June 1825 he was accepted to lecture on his partial proof for the case  at the French Academy of Sciences
at the French Academy of Sciences
, an exceptional feat for a 20 year old student with no degree. His lecture at the Academy has also put Dirichlet in close contact with Fourier
and Poisson
, who raised his interest in theoretical physics, especially Fourier's analytic theory of heat
.
, who had been called to join the court of King Friedrich Wilhelm III
. Humboldt, planning to make Berlin a center of science and research, immediately offered his help to Dirichlet, sending letters in his favour to the Prussian government and to the Prussian Academy of Sciences
. Humboldt also secured a recommendation letter from Gauss, who upon reading his memoir on Fermat's theorem wrote with an unusual amount of praise that "Dirichlet showed excellent talent". With the support of Humboldt and Gauss, Dirichlet was offered a teaching position at the University of Breslau (now the University of Wrocław in Poland
). However, as he had not passed a doctoral disertation, he submitted his memoir on the Fermat theorem as a thesis to the University of Bonn
. Again his lack of fluency in Latin rendered him unable to hold the required public disputation of his thesis; after much discussion, the University decided to bypass the problem by awarding him a honorary doctorate in February 1827. Also, the Minister of education granted him a dispensation for the Latin disputation required for the Habilitation
. Dirichlet earned the Habilitation and lectured in the 1827/28 year as a Privatdozent
at Breslau.
While in Breslau, Dirichlet continued his number theoretic research, publishing important contributions to the biquadratic reciprocity
law which at the time was a focal point of Gauss' research. Alexander von Humboldt took advantage of these new results, which had also drawn enthusiastic praise from Friedrich Bessel
, to arrange for him the desired transfer to Berlin. Given Dirichlet's young age (he was 23 years old at the time), Humboldt was only able to get him a trial position at the Prussian Military Academy in Berlin while remaining nominally employed by the University of Breslau. The probation was extended for three years until the position becoming definitive in 1831.
s held by the Mendelssohn family
, a distinguished German family headed by banker Abraham Mendelssohn Bartholdy
. Their house was a weekly gathering point of the Berlin artists and scientists, including family members Felix Mendelssohn Bartholdy and Fanny Mendelssohn
, both famous composers, or painter Wilhelm Hensel
(Fanny's husband). Dirichlet showed great interest in Rebecka Mendelssohn, a daughter of Abraham, whom he married in 1832. In 1833 their first son, Walter, was born.
As soon as he came to Berlin, Dirichlet applied to lecture at the University of Berlin
, and the Education Minister approved the transfer and in 1831 assigned him to the faculty of philosophy. The faculty required a Habilitation again and although Dirichlet wrote a Habilitationsschrift as needed, he postponed giving the mandatory lecture in Latin for another 20 years, until 1851. For not completing these formal requirements, he remained attached to the faculty with less than full rights, including limited payment, forced him to keep in parallel his teaching position at the Military School. In 1832 Dirichlet became a member of the Prussian Academy of Sciences
, the youngest member at only 27 years old.
Dirichlet had a good reputation with students for the clarity of his explanations and enjoyed teaching, especially as his University lectures tended to be on the more advanced topics in which he was doing research: number theory (he was the first German professor to give lectures on number theory), analysis and mathematical physics. He advised the doctoral thesis of several important German mathematicians, as Gotthold Eisenstein, Leopold Kronecker
, Rudolf Lipschitz
and Carl Wilhelm Borchardt
, while being influential in the mathematical formation of many other scientists, including Elwin Bruno Christoffel
, Wilhelm Weber
, Eduard Heine
, Ludwig von Seidel
and Julius Weingarten
. At the Military Academy Dirichlet managed to introduce differential
and integral calculus in the curriculum, significantly raising the level of scientific education there. However, in time he started feeling that his double teaching load, at the Military academy and at the University, started weighing down on the time available for his research.
While in Berlin, Dirichlet kept in contact with other mathematicians. In 1829, during a trip, he met Jacobi, at the time professor of mathematics at Königsberg University. Over the years they kept meeting and corresponding on research matters, in time becoming close friends. In 1839, during a visit to Paris, Dirichlet met Joseph Liouville
, the two mathematicians becoming friends, keeping in contact and even visiting each other with the families a few years later. in 1839, Jacobi sent Dirichlet a paper by Ernst Kummer
, at the time a school teacher. Realizing Kummer's potential, they helped him get elected in the Berlin Academy and, in 1842, obtained for him a full professor position at the University of Breslau. In 1840 Kummer married Ottilie Mendelssohn, a cousin of Rebecka.
In 1843, when Jacobi fell ill, Dirichlet traveled to Königsberg to help him, then obtained for him the assistance of King Friedrich Wilhelm IV
's personal physician. When the medic recommended Jacobi to spend some time in Italy, he joined him on the trip together with his family. They were accompanied to Italy by Ludwig Schläfli
, who came as a translator; as he was strongly interested in mathematics, during the trip both Dirichlet and Jacobi lectured him, later Schläfli becoming an important mathematician himself. The Dirichlet family extended their stay in Italy to 1845, their daughter Flora being born there. In 1844, Jacobi moved to Berlin as a royal pensioner, their friendship becoming even closer. In 1846, when the Heidelberg University tried to recruit Dirichlet, Jacobi provided von Humboldt the needed support in order to obtain a doubling of Dirichlet's pay at the University in order to keep him in Berlin; however, even now he wasn't paid a full professor wage and he could not leave the Military Academy.
Holding liberal views, Dirichlet and his family supported the 1848 revolution
; he even guarded with a rifle the palace of the Prince of Prussia. After the revolution failed, the Military Academy closed temporarily, causing him a large loss of income. When it reopened, the environment became more hostile to him as the officers he was teaching were naturally reactionary. Also the conservatory press pointed him out, as well as Jacobi and other liberal professors, as "the red contingent of the staff".
In 1849 Dirichlet participated, together with his friend Jacobi, to the jubilee of Gauss' doctorate.
Dirichlet enjoyed his time in Göttingen as the lighter teaching load allowed him more time for research and, also, he got in close contact with the new generation of researchers, especially Richard Dedekind
and Bernhard Riemann
. After moving to Göttingen he was able to obtain a small annual payment for Riemann in order to retain him in the teaching staff there. Dedekind, Riemann, Moritz Cantor
and Alfred Enneper
, although they had all already earned they PhDs, attended Dirichlet's classes to study with him. Dedekind, who felt that there were significant gaps at the time in his mathematics education, considered that the occasion to study with Dirichlet made him "a new human being". He later edited and published Dirichlet's lectures and other results in number theory
under the title (Lectures on Number Theory).
In the summer of 1858, during a trip to Montreux
, Dirichlet suffered a heart attack. On 5 May 1859, he died in Göttingen, several months after the death of his wife Rebecka. Dirichlet's brain is preserved in the department of physiology at the University of Göttingen, along with the brain of Gauss. The Academy in Berlin honored him with a formal memorial speech held by Kummer in 1860, and later ordered the publication of his collected works edited by Kronecker and Lazarus Fuchs
.
was Dirichlet's main research interest, a field in which he found several deep results and in proving them introduced some fundamental tools, many of which were later named after him. In 1837 he published Dirichlet's theorem on arithmetic progressions
, using mathematical analysis
concepts to tackle an algebraic problem and thus creating the branch of analytic number theory
. In proving the theorem, he introduced the Dirichlet character
s and L-functions. Also, in the article he noted the difference between the absolute
and conditional convergence of series
and its impact in what was later called the Riemann series theorem. In 1841 he generalized his arithmetic progressions theorem from integers to the ring
of Gaussian integer
s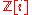 .
.
In a couple of papers in 1838 and 1839 he proved the first class number formula
, for quadratic form
s (later refined by his student Kronecker). The formula, which Jacobi called a result "touching the utmost of human acumen", opened the way for similar results regarding more general number fields. Based on his research of the structure of the unit group of quadratic field
s, he proved the Dirichlet unit theorem, a fundamental result in algebraic number theory
.
He first used the pigeonhole principle, a basic counting argument, in the proof of a theorem in diophantine approximation
, later named after him Dirichlet's approximation theorem
. He published important contributions to Fermat's last theorem
, for which he proved the cases n=5 and n=14, and to the biquadratic reciprocity law
. The Dirichlet divisor problem, for which he found the first results, is still an unsolved problem in number theory despite later contributions by other researchers.
, showing for which functions the convergence of the Fourier series
holds. Before Dirichlet's solution, not only Fourier, but also Poisson and Cauchy had tried unsuccessfully to find a rigorous proof of convergence. The memoir pointed out Cauchy's mistake and introduced Dirichlet's test
for the convergence of series. It also introduced the Dirichlet function as an example that not any function is integrable (the definite integral was still a developing topic at the time) and, in the proof of the theorem for the Forier series, introduced the Dirichlet kernel and the Dirichlet integral
.
Dirichlet also studied the first boundary value problem
, for the Laplace equation, proving the unicity of the solution; this type of problem in the theory of partial differential equation
s was later named the Dirichlet problem
after him. In the proof he notably used the principle that the solution is the function that minimizes the so-called Dirichlet energy. Riemann later named this approach the Dirichlet principle, although he knew it had also been used by Gauss and by Lord Kelvin
.
by the property that "to any x there corresponds a single finite y", but then restricts his attention to piecewise continuous functions. Based on this, he is credited with introducing the modern concept for a function, as opposed to the older vague understanding of a function as an analytic formula. Imre Lakatos
cites Hermann Hankel
as the early origin of this attribution, but disputes the claim saying that "there is ample evidence that he had no idea of this concept [...] for instance, when he discusses piecewise continuous functions, he says that at points of discontinuity the function has two values".
, lecturing and publishing research in potential theory
(including the Dirichlet problem and Dirichlet priciple mentioned above), the theory of heat
and hydrodynamics. He improved on Lagrange
's work on conservative systems by showing that the condition for equilibrium
is that the potential energy
is minimal.
Although he didn't publish much in the field, Dirichlet lectured on probability theory
and least squares
, introducing some original methods and results, in particular for limit theorems
and an improvement of Laplace's method of approximation related to the central limit theorem
. The Dirichlet distribution and the Dirichlet process
, based on the Dirichlet integral, are named after him.
In 1855 Dirichlet was awarded the civil class medal of the Pour le Mérite
order at von Humboldt's recommendation. The Dirichlet crater
on the Moon
and the 11665 Dirichlet
asteroid are named after him.
Germany
Germany , officially the Federal Republic of Germany , is a federal parliamentary republic in Europe. The country consists of 16 states while the capital and largest city is Berlin. Germany covers an area of 357,021 km2 and has a largely temperate seasonal climate...
mathematician
Mathematician
A mathematician is a person whose primary area of study is the field of mathematics. Mathematicians are concerned with quantity, structure, space, and change....
with deep contributions to number theory
Number theory
Number theory is a branch of pure mathematics devoted primarily to the study of the integers. Number theorists study prime numbers as well...
(including creating the field of analytic number theory
Analytic number theory
In mathematics, analytic number theory is a branch of number theory that uses methods from mathematical analysis to solve problems about the integers. It is often said to have begun with Dirichlet's introduction of Dirichlet L-functions to give the first proof of Dirichlet's theorem on arithmetic...
), as well as to the theory of Fourier series
Fourier series
In mathematics, a Fourier series decomposes periodic functions or periodic signals into the sum of a set of simple oscillating functions, namely sines and cosines...
and other topics in mathematical analysis
Mathematical analysis
Mathematical analysis, which mathematicians refer to simply as analysis, has its beginnings in the rigorous formulation of infinitesimal calculus. It is a branch of pure mathematics that includes the theories of differentiation, integration and measure, limits, infinite series, and analytic functions...
; he is credited with being one of the first mathematicians to give the modern formal definition of a function
Function (mathematics)
In mathematics, a function associates one quantity, the argument of the function, also known as the input, with another quantity, the value of the function, also known as the output. A function assigns exactly one output to each input. The argument and the value may be real numbers, but they can...
.
Early life (1805-22)
Gustav Lejeune Dirichlet was born on 13 February 1805 in a German family in DürenDüren
Düren is a town in North Rhine-Westphalia, capital of Düren district. It is located between Aachen and Cologne on the river Rur.-Roman era:Celts inhabited Düren's area before the Romans. They called their small settlement Durum . After the Celts other Germanic tribes settled this area...
, a town on the left bank of the Rhine which at the time was part of the First French Empire
First French Empire
The First French Empire , also known as the Greater French Empire or Napoleonic Empire, was the empire of Napoleon I of France...
, reverting to Prussia
Prussia
Prussia was a German kingdom and historic state originating out of the Duchy of Prussia and the Margraviate of Brandenburg. For centuries, the House of Hohenzollern ruled Prussia, successfully expanding its size by way of an unusually well-organized and effective army. Prussia shaped the history...
after the Congress of Vienna
Congress of Vienna
The Congress of Vienna was a conference of ambassadors of European states chaired by Klemens Wenzel von Metternich, and held in Vienna from September, 1814 to June, 1815. The objective of the Congress was to settle the many issues arising from the French Revolutionary Wars, the Napoleonic Wars,...
in 1815. His father Johann Arnold Lejeune Dirichlet was the postmaster, merchant, and city councilor. His paternal grandfather had come to Düren from Richelette, a small community 5 km north east of Liège
Liège
Liège is a major city and municipality of Belgium located in the province of Liège, of which it is the economic capital, in Wallonia, the French-speaking region of Belgium....
in Belgium
Belgium
Belgium , officially the Kingdom of Belgium, is a federal state in Western Europe. It is a founding member of the European Union and hosts the EU's headquarters, and those of several other major international organisations such as NATO.Belgium is also a member of, or affiliated to, many...
, from which his surname "Lejeune Dirichlet" ("", French
French language
French is a Romance language spoken as a first language in France, the Romandy region in Switzerland, Wallonia and Brussels in Belgium, Monaco, the regions of Quebec and Acadia in Canada, and by various communities elsewhere. Second-language speakers of French are distributed throughout many parts...
for "the youth from Richelette") was derived.
Although his family was not wealthy and he was the youngest of seven children, his parents supported his education. They enrolled him in an elementary school and then private school in hope that he would later become a merchant. The young Dirichlet, who showed a strong interest in mathematics before age 12, convinced his parents to allow him to continue his studies. In 1817 they sent him to the Gymnasium in Bonn under the care of Peter Joseph Elvenich
Peter Joseph Elvenich
Peter Joseph Elvenich was a German Catholic theologian and philosopher who was born in Embken, a village that today is part of Nideggen, North Rhine-Westphalia...
, a student his family knew. In 1820 Dirichlet moved to the Jesuit Gymnasium
Dreikönigsgymnasium
The Dreikönigsgymnasium is a regular public Gymnasium located in Cologne, Germany. Founded in 1450 it is the oldest school in Cologne and one of the oldest in Germany.-Alumni:...
in Cologne
Cologne
Cologne is Germany's fourth-largest city , and is the largest city both in the Germany Federal State of North Rhine-Westphalia and within the Rhine-Ruhr Metropolitan Area, one of the major European metropolitan areas with more than ten million inhabitants.Cologne is located on both sides of the...
, where his lessons with Georg Ohm
Georg Ohm
Georg Simon Ohm was a German physicist. As a high school teacher, Ohm began his research with the recently-invented electrochemical cell, invented by Italian Count Alessandro Volta. Using equipment of his own creation, Ohm determined that there is a direct proportionality between the potential...
helped widen his knowledge in mathematics. He left the gymnasium a year later with only a certificate, as his inability to speak fluent Latin prevented him from earning the Abitur
Abitur
Abitur is a designation used in Germany, Finland and Estonia for final exams that pupils take at the end of their secondary education, usually after 12 or 13 years of schooling, see also for Germany Abitur after twelve years.The Zeugnis der Allgemeinen Hochschulreife, often referred to as...
.
Studies in Paris (1822-26)
Dirichlet again convinced his parents to provide further financial support for his studies in mathematics, against their wish for a career in law. As Germany provided little opportunity to study higher mathematics at the time, with only GaussCarl Friedrich Gauss
Johann Carl Friedrich Gauss was a German mathematician and scientist who contributed significantly to many fields, including number theory, statistics, analysis, differential geometry, geodesy, geophysics, electrostatics, astronomy and optics.Sometimes referred to as the Princeps mathematicorum...
at the University of Göttingen who was nominally a professor of astronomy and anyway disliked teaching, Dirichlet decided to go to Paris
Paris
Paris is the capital and largest city in France, situated on the river Seine, in northern France, at the heart of the Île-de-France region...
in May 1822. There he attended classes at the Collège de France
Collège de France
The Collège de France is a higher education and research establishment located in Paris, France, in the 5th arrondissement, or Latin Quarter, across the street from the historical campus of La Sorbonne at the intersection of Rue Saint-Jacques and Rue des Écoles...
and at the Faculté des sciences de Paris, learning mathematics from Hachette
Jean Nicolas Pierre Hachette
Jean Nicolas Pierre Hachette , French mathematician, was born at Mézières, where his father was a bookseller.For his early education he proceeded first to the college of Charleville, and afterwards to that of Reims...
among others, while undertaking private study of Gauss' Disquisitiones Arithmeticae
Disquisitiones Arithmeticae
The Disquisitiones Arithmeticae is a textbook of number theory written in Latin by Carl Friedrich Gauss in 1798 when Gauss was 21 and first published in 1801 when he was 24...
, a book he kept close for his entire life. In 1823 he was recommended to General Foy
Maximilien Sebastien Foy
Maximilien Sébastien Foy was a French military leader, statesman and writer.-Revolution:He was born in Ham, Somme, and educated in the military school of La Fere, and made sub-lieutenant of artillery in 1792. He was present at the battles of Valmy and Jemappes, and in 1793 obtained a company, as...
, who hired him as a private tutor to teach his children German, the wage finally allowing Dirichlet to become independent from his parents' financial support.
His first original research, comprising part of a proof of Fermat's last theorem
Fermat's Last Theorem
In number theory, Fermat's Last Theorem states that no three positive integers a, b, and c can satisfy the equation an + bn = cn for any integer value of n greater than two....
for the case
 , brought him immediate fame, being the first advance in the theorem since Fermat
, brought him immediate fame, being the first advance in the theorem since FermatPierre de Fermat
Pierre de Fermat was a French lawyer at the Parlement of Toulouse, France, and an amateur mathematician who is given credit for early developments that led to infinitesimal calculus, including his adequality...
's own proof of the case
 and Euler
and EulerLeonhard Euler
Leonhard Euler was a pioneering Swiss mathematician and physicist. He made important discoveries in fields as diverse as infinitesimal calculus and graph theory. He also introduced much of the modern mathematical terminology and notation, particularly for mathematical analysis, such as the notion...
's proof for
 . Adrien-Marie Legendre
. Adrien-Marie LegendreAdrien-Marie Legendre
Adrien-Marie Legendre was a French mathematician.The Moon crater Legendre is named after him.- Life :...
, one of the referees, soon completed the proof for this case; Dirichlet completed his own proof a short time after Legendre, and a few years later produced a full proof for the case
 . In June 1825 he was accepted to lecture on his partial proof for the case
. In June 1825 he was accepted to lecture on his partial proof for the case  at the French Academy of Sciences
at the French Academy of SciencesFrench Academy of Sciences
The French Academy of Sciences is a learned society, founded in 1666 by Louis XIV at the suggestion of Jean-Baptiste Colbert, to encourage and protect the spirit of French scientific research...
, an exceptional feat for a 20 year old student with no degree. His lecture at the Academy has also put Dirichlet in close contact with Fourier
Joseph Fourier
Jean Baptiste Joseph Fourier was a French mathematician and physicist best known for initiating the investigation of Fourier series and their applications to problems of heat transfer and vibrations. The Fourier transform and Fourier's Law are also named in his honour...
and Poisson
Siméon Denis Poisson
Siméon Denis Poisson , was a French mathematician, geometer, and physicist. He however, was the final leading opponent of the wave theory of light as a member of the elite l'Académie française, but was proven wrong by Augustin-Jean Fresnel.-Biography:...
, who raised his interest in theoretical physics, especially Fourier's analytic theory of heat
Heat equation
The heat equation is an important partial differential equation which describes the distribution of heat in a given region over time...
.
Back to Prussia, Breslau (1825-28)
As General Foy died in November 1825 and he could not find any paying position in France, Dirichlet had to return to Prussia. Fourier and Poisson introduced him to Alexander von HumboldtAlexander von Humboldt
Friedrich Wilhelm Heinrich Alexander Freiherr von Humboldt was a German naturalist and explorer, and the younger brother of the Prussian minister, philosopher and linguist Wilhelm von Humboldt...
, who had been called to join the court of King Friedrich Wilhelm III
Frederick William III of Prussia
Frederick William III was king of Prussia from 1797 to 1840. He was in personal union the sovereign prince of the Principality of Neuchâtel .-Early life:...
. Humboldt, planning to make Berlin a center of science and research, immediately offered his help to Dirichlet, sending letters in his favour to the Prussian government and to the Prussian Academy of Sciences
Prussian Academy of Sciences
The Prussian Academy of Sciences was an academy established in Berlin on 11 July 1700, four years after the Akademie der Künste or "Arts Academy", to which "Berlin Academy" may also refer.-Origins:...
. Humboldt also secured a recommendation letter from Gauss, who upon reading his memoir on Fermat's theorem wrote with an unusual amount of praise that "Dirichlet showed excellent talent". With the support of Humboldt and Gauss, Dirichlet was offered a teaching position at the University of Breslau (now the University of Wrocław in Poland
Poland
Poland , officially the Republic of Poland , is a country in Central Europe bordered by Germany to the west; the Czech Republic and Slovakia to the south; Ukraine, Belarus and Lithuania to the east; and the Baltic Sea and Kaliningrad Oblast, a Russian exclave, to the north...
). However, as he had not passed a doctoral disertation, he submitted his memoir on the Fermat theorem as a thesis to the University of Bonn
University of Bonn
The University of Bonn is a public research university located in Bonn, Germany. Founded in its present form in 1818, as the linear successor of earlier academic institutions, the University of Bonn is today one of the leading universities in Germany. The University of Bonn offers a large number...
. Again his lack of fluency in Latin rendered him unable to hold the required public disputation of his thesis; after much discussion, the University decided to bypass the problem by awarding him a honorary doctorate in February 1827. Also, the Minister of education granted him a dispensation for the Latin disputation required for the Habilitation
Habilitation
Habilitation is the highest academic qualification a scholar can achieve by his or her own pursuit in several European and Asian countries. Earned after obtaining a research doctorate, such as a PhD, habilitation requires the candidate to write a professorial thesis based on independent...
. Dirichlet earned the Habilitation and lectured in the 1827/28 year as a Privatdozent
Privatdozent
Privatdozent or Private lecturer is a title conferred in some European university systems, especially in German-speaking countries, for someone who pursues an academic career and holds all formal qualifications to become a tenured university professor...
at Breslau.
While in Breslau, Dirichlet continued his number theoretic research, publishing important contributions to the biquadratic reciprocity
Quartic reciprocity
Quartic or biquadratic reciprocity is a collection of theorems in elementary and algebraic number theory that state conditions under which the congruence x4 ≡ p is solvable; the word "reciprocity" comes from the form of some of these theorems, in that they relate the solvability of the...
law which at the time was a focal point of Gauss' research. Alexander von Humboldt took advantage of these new results, which had also drawn enthusiastic praise from Friedrich Bessel
Friedrich Bessel
-References:* John Frederick William Herschel, A brief notice of the life, researches, and discoveries of Friedrich Wilhelm Bessel, London: Barclay, 1847 -External links:...
, to arrange for him the desired transfer to Berlin. Given Dirichlet's young age (he was 23 years old at the time), Humboldt was only able to get him a trial position at the Prussian Military Academy in Berlin while remaining nominally employed by the University of Breslau. The probation was extended for three years until the position becoming definitive in 1831.
Berlin (1826-1855)
After moving to Berlin, Humboldt introduced Dirichlet to the great salonSalon (gathering)
A salon is a gathering of people under the roof of an inspiring host, held partly to amuse one another and partly to refine taste and increase their knowledge of the participants through conversation. These gatherings often consciously followed Horace's definition of the aims of poetry, "either to...
s held by the Mendelssohn family
Mendelssohn family
The Mendelssohn family are the descendants of the German Jewish philosopher Moses Mendelssohn, and include his grandson, the composer Felix Mendelssohn....
, a distinguished German family headed by banker Abraham Mendelssohn Bartholdy
Abraham Mendelssohn Bartholdy
Abraham Ernst Mendelssohn Bartholdy was a German Jewish banker and philanthropist...
. Their house was a weekly gathering point of the Berlin artists and scientists, including family members Felix Mendelssohn Bartholdy and Fanny Mendelssohn
Fanny Mendelssohn
Fanny Cäcilie Mendelssohn , later Fanny Hensel, was a German pianist and composer, the sister of the composer Felix Mendelssohn and granddaughter of the philosopher Moses Mendelssohn...
, both famous composers, or painter Wilhelm Hensel
Wilhelm Hensel
Wilhelm Hensel was a German painter, brother of Luise Hensel, husband to Fanny Mendelssohn, and brother-in-law to Felix Mendelssohn....
(Fanny's husband). Dirichlet showed great interest in Rebecka Mendelssohn, a daughter of Abraham, whom he married in 1832. In 1833 their first son, Walter, was born.
As soon as he came to Berlin, Dirichlet applied to lecture at the University of Berlin
Humboldt University of Berlin
The Humboldt University of Berlin is Berlin's oldest university, founded in 1810 as the University of Berlin by the liberal Prussian educational reformer and linguist Wilhelm von Humboldt, whose university model has strongly influenced other European and Western universities...
, and the Education Minister approved the transfer and in 1831 assigned him to the faculty of philosophy. The faculty required a Habilitation again and although Dirichlet wrote a Habilitationsschrift as needed, he postponed giving the mandatory lecture in Latin for another 20 years, until 1851. For not completing these formal requirements, he remained attached to the faculty with less than full rights, including limited payment, forced him to keep in parallel his teaching position at the Military School. In 1832 Dirichlet became a member of the Prussian Academy of Sciences
Prussian Academy of Sciences
The Prussian Academy of Sciences was an academy established in Berlin on 11 July 1700, four years after the Akademie der Künste or "Arts Academy", to which "Berlin Academy" may also refer.-Origins:...
, the youngest member at only 27 years old.
Dirichlet had a good reputation with students for the clarity of his explanations and enjoyed teaching, especially as his University lectures tended to be on the more advanced topics in which he was doing research: number theory (he was the first German professor to give lectures on number theory), analysis and mathematical physics. He advised the doctoral thesis of several important German mathematicians, as Gotthold Eisenstein, Leopold Kronecker
Leopold Kronecker
Leopold Kronecker was a German mathematician who worked on number theory and algebra.He criticized Cantor's work on set theory, and was quoted by as having said, "God made integers; all else is the work of man"...
, Rudolf Lipschitz
Rudolf Lipschitz
Rudolf Otto Sigismund Lipschitz was a German mathematician and professor at the University of Bonn from 1864. Peter Gustav Dirichlet was his teacher. He supervised the early work of Felix Klein....
and Carl Wilhelm Borchardt
Carl Wilhelm Borchardt
Carl Wilhelm Borchardt was a German mathematician.Borchardt was born to a Jewish family in Berlin. His father, Moritz, was a respected merchant, and his mother was Emma Heilborn. Borchardt studied under a number of tutors, including Julius Plücker and Jakob Steiner...
, while being influential in the mathematical formation of many other scientists, including Elwin Bruno Christoffel
Elwin Bruno Christoffel
Elwin Bruno Christoffel was a German mathematician and physicist.-Life:...
, Wilhelm Weber
Wilhelm Eduard Weber
Wilhelm Eduard Weber was a German physicist and, together with Carl Friedrich Gauss, inventor of the first electromagnetic telegraph.-Early years:...
, Eduard Heine
Eduard Heine
Heinrich Eduard Heine was a German mathematician.Heine became known for results on special functions and in real analysis. In particular, he authored an important treatise on spherical harmonics and Legendre functions . He also investigated basic hypergeometric series...
, Ludwig von Seidel
Philipp Ludwig von Seidel
Philipp Ludwig von Seidel was a German mathematician. His mother was Julie Reinhold and his father was Justus Christian Felix Seidel.Lakatos credits von Seidel with discovering, in 1847, the crucial analytic concept of uniform convergence, while analyzing an incorrect proof of Cauchy's.In 1857,...
and Julius Weingarten
Julius Weingarten
Julius Weingarten was a German mathematician. He made some important contributions to the differential geometry of surfaces, such as theWeingarten equations.-External links:...
. At the Military Academy Dirichlet managed to introduce differential
Differential calculus
In mathematics, differential calculus is a subfield of calculus concerned with the study of the rates at which quantities change. It is one of the two traditional divisions of calculus, the other being integral calculus....
and integral calculus in the curriculum, significantly raising the level of scientific education there. However, in time he started feeling that his double teaching load, at the Military academy and at the University, started weighing down on the time available for his research.
While in Berlin, Dirichlet kept in contact with other mathematicians. In 1829, during a trip, he met Jacobi, at the time professor of mathematics at Königsberg University. Over the years they kept meeting and corresponding on research matters, in time becoming close friends. In 1839, during a visit to Paris, Dirichlet met Joseph Liouville
Joseph Liouville
- Life and work :Liouville graduated from the École Polytechnique in 1827. After some years as an assistant at various institutions including the Ecole Centrale Paris, he was appointed as professor at the École Polytechnique in 1838...
, the two mathematicians becoming friends, keeping in contact and even visiting each other with the families a few years later. in 1839, Jacobi sent Dirichlet a paper by Ernst Kummer
Ernst Kummer
Ernst Eduard Kummer was a German mathematician. Skilled in applied mathematics, Kummer trained German army officers in ballistics; afterwards, he taught for 10 years in a gymnasium, the German equivalent of high school, where he inspired the mathematical career of Leopold Kronecker.-Life:Kummer...
, at the time a school teacher. Realizing Kummer's potential, they helped him get elected in the Berlin Academy and, in 1842, obtained for him a full professor position at the University of Breslau. In 1840 Kummer married Ottilie Mendelssohn, a cousin of Rebecka.
In 1843, when Jacobi fell ill, Dirichlet traveled to Königsberg to help him, then obtained for him the assistance of King Friedrich Wilhelm IV
Frederick William IV of Prussia
|align=right|Upon his accession, he toned down the reactionary policies enacted by his father, easing press censorship and promising to enact a constitution at some point, but he refused to enact a popular legislative assembly, preferring to work with the aristocracy through "united committees" of...
's personal physician. When the medic recommended Jacobi to spend some time in Italy, he joined him on the trip together with his family. They were accompanied to Italy by Ludwig Schläfli
Ludwig Schläfli
Ludwig Schläfli was a Swiss geometer and complex analyst who was one of the key figures in developing the notion of higher dimensional spaces. The concept of multidimensionality has since come to play a pivotal role in physics, and is a common element in science fiction...
, who came as a translator; as he was strongly interested in mathematics, during the trip both Dirichlet and Jacobi lectured him, later Schläfli becoming an important mathematician himself. The Dirichlet family extended their stay in Italy to 1845, their daughter Flora being born there. In 1844, Jacobi moved to Berlin as a royal pensioner, their friendship becoming even closer. In 1846, when the Heidelberg University tried to recruit Dirichlet, Jacobi provided von Humboldt the needed support in order to obtain a doubling of Dirichlet's pay at the University in order to keep him in Berlin; however, even now he wasn't paid a full professor wage and he could not leave the Military Academy.
Holding liberal views, Dirichlet and his family supported the 1848 revolution
Revolutions of 1848 in the German states
The Revolutions of 1848 in the German states, also called the March Revolution – part of the Revolutions of 1848 that broke out in many countries of Europe – were a series of loosely coordinated protests and rebellions in the states of the German Confederation, including the Austrian Empire...
; he even guarded with a rifle the palace of the Prince of Prussia. After the revolution failed, the Military Academy closed temporarily, causing him a large loss of income. When it reopened, the environment became more hostile to him as the officers he was teaching were naturally reactionary. Also the conservatory press pointed him out, as well as Jacobi and other liberal professors, as "the red contingent of the staff".
In 1849 Dirichlet participated, together with his friend Jacobi, to the jubilee of Gauss' doctorate.
Göttingen (1855-59)
Despite Dirichlet's expertise and the honours he received, and although by 1851 he had finally completed all formal requirements for a full professor, the issue of raising his payment at the University still dragged and he still couldn't leave the Military Academy. In 1855, upon Gauss' death, the University of Göttingen decided to call Dirichlet as his successor. Given the difficulties faced in Berlin, he decided to accept the offer and immediately moved to Göttingen with his family. Kummer was called to follow him as a mathematics professor in Berlin.Dirichlet enjoyed his time in Göttingen as the lighter teaching load allowed him more time for research and, also, he got in close contact with the new generation of researchers, especially Richard Dedekind
Richard Dedekind
Julius Wilhelm Richard Dedekind was a German mathematician who did important work in abstract algebra , algebraic number theory and the foundations of the real numbers.-Life:...
and Bernhard Riemann
Bernhard Riemann
Georg Friedrich Bernhard Riemann was an influential German mathematician who made lasting contributions to analysis and differential geometry, some of them enabling the later development of general relativity....
. After moving to Göttingen he was able to obtain a small annual payment for Riemann in order to retain him in the teaching staff there. Dedekind, Riemann, Moritz Cantor
Moritz Cantor
Moritz Benedikt Cantor was a German historian of mathematics.He was born at Mannheim, Germany. He came from a family that had emigrated to the Netherlands from Portugal, another branch of which had established itself in Russia, where Georg Cantor was born...
and Alfred Enneper
Alfred Enneper
Alfred Enneper earned his PhD from the Georg-August-Universität Göttingen in 1856 for his dissertation about functions with complex arguments. After his habilitation 1859 in Göttingen he was from 1870 on Professor at Göttingen. He studied minimal surfaces and parametrized Enneper's minimal...
, although they had all already earned they PhDs, attended Dirichlet's classes to study with him. Dedekind, who felt that there were significant gaps at the time in his mathematics education, considered that the occasion to study with Dirichlet made him "a new human being". He later edited and published Dirichlet's lectures and other results in number theory
Number theory
Number theory is a branch of pure mathematics devoted primarily to the study of the integers. Number theorists study prime numbers as well...
under the title (Lectures on Number Theory).
In the summer of 1858, during a trip to Montreux
Montreux
Montreux is a municipality in the district of Riviera-Pays-d'Enhaut in the canton of Vaud in Switzerland.It is located on Lake Geneva at the foot of the Alps and has a population, , of and nearly 90,000 in the agglomeration.- History :...
, Dirichlet suffered a heart attack. On 5 May 1859, he died in Göttingen, several months after the death of his wife Rebecka. Dirichlet's brain is preserved in the department of physiology at the University of Göttingen, along with the brain of Gauss. The Academy in Berlin honored him with a formal memorial speech held by Kummer in 1860, and later ordered the publication of his collected works edited by Kronecker and Lazarus Fuchs
Lazarus Fuchs
Lazarus Immanuel Fuchs was a German mathematician who contributed important research in the field of linear differential equations...
.
Number theory
Number theoryNumber theory
Number theory is a branch of pure mathematics devoted primarily to the study of the integers. Number theorists study prime numbers as well...
was Dirichlet's main research interest, a field in which he found several deep results and in proving them introduced some fundamental tools, many of which were later named after him. In 1837 he published Dirichlet's theorem on arithmetic progressions
Dirichlet's theorem on arithmetic progressions
In number theory, Dirichlet's theorem, also called the Dirichlet prime number theorem, states that for any two positive coprime integers a and d, there are infinitely many primes of the form a + nd, where n ≥ 0. In other words, there are infinitely many primes which are...
, using mathematical analysis
Mathematical analysis
Mathematical analysis, which mathematicians refer to simply as analysis, has its beginnings in the rigorous formulation of infinitesimal calculus. It is a branch of pure mathematics that includes the theories of differentiation, integration and measure, limits, infinite series, and analytic functions...
concepts to tackle an algebraic problem and thus creating the branch of analytic number theory
Analytic number theory
In mathematics, analytic number theory is a branch of number theory that uses methods from mathematical analysis to solve problems about the integers. It is often said to have begun with Dirichlet's introduction of Dirichlet L-functions to give the first proof of Dirichlet's theorem on arithmetic...
. In proving the theorem, he introduced the Dirichlet character
Dirichlet character
In number theory, Dirichlet characters are certain arithmetic functions which arise from completely multiplicative characters on the units of \mathbb Z / k \mathbb Z...
s and L-functions. Also, in the article he noted the difference between the absolute
Absolute convergence
In mathematics, a series of numbers is said to converge absolutely if the sum of the absolute value of the summand or integrand is finite...
and conditional convergence of series
Series (mathematics)
A series is the sum of the terms of a sequence. Finite sequences and series have defined first and last terms, whereas infinite sequences and series continue indefinitely....
and its impact in what was later called the Riemann series theorem. In 1841 he generalized his arithmetic progressions theorem from integers to the ring
Ring (mathematics)
In mathematics, a ring is an algebraic structure consisting of a set together with two binary operations usually called addition and multiplication, where the set is an abelian group under addition and a semigroup under multiplication such that multiplication distributes over addition...
of Gaussian integer
Gaussian integer
In number theory, a Gaussian integer is a complex number whose real and imaginary part are both integers. The Gaussian integers, with ordinary addition and multiplication of complex numbers, form an integral domain, usually written as Z[i]. The Gaussian integers are a special case of the quadratic...
s
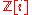 .
.In a couple of papers in 1838 and 1839 he proved the first class number formula
Class number formula
In number theory, the class number formula relates many important invariants of a number field to a special value of its Dedekind zeta function-General statement of the class number formula:...
, for quadratic form
Quadratic form
In mathematics, a quadratic form is a homogeneous polynomial of degree two in a number of variables. For example,4x^2 + 2xy - 3y^2\,\!is a quadratic form in the variables x and y....
s (later refined by his student Kronecker). The formula, which Jacobi called a result "touching the utmost of human acumen", opened the way for similar results regarding more general number fields. Based on his research of the structure of the unit group of quadratic field
Quadratic field
In algebraic number theory, a quadratic field is an algebraic number field K of degree two over Q. It is easy to show that the map d ↦ Q is a bijection from the set of all square-free integers d ≠ 0, 1 to the set of all quadratic fields...
s, he proved the Dirichlet unit theorem, a fundamental result in algebraic number theory
Algebraic number theory
Algebraic number theory is a major branch of number theory which studies algebraic structures related to algebraic integers. This is generally accomplished by considering a ring of algebraic integers O in an algebraic number field K/Q, and studying their algebraic properties such as factorization,...
.
He first used the pigeonhole principle, a basic counting argument, in the proof of a theorem in diophantine approximation
Diophantine approximation
In number theory, the field of Diophantine approximation, named after Diophantus of Alexandria, deals with the approximation of real numbers by rational numbers....
, later named after him Dirichlet's approximation theorem
Dirichlet's approximation theorem
In number theory, Dirichlet's theorem on Diophantine approximation, also called Dirichlet's approximation theorem, states that for any real number α and any positive integer N, there exists integers p and q such that 1 ≤ q ≤ N and...
. He published important contributions to Fermat's last theorem
Fermat's Last Theorem
In number theory, Fermat's Last Theorem states that no three positive integers a, b, and c can satisfy the equation an + bn = cn for any integer value of n greater than two....
, for which he proved the cases n=5 and n=14, and to the biquadratic reciprocity law
Quartic reciprocity
Quartic or biquadratic reciprocity is a collection of theorems in elementary and algebraic number theory that state conditions under which the congruence x4 ≡ p is solvable; the word "reciprocity" comes from the form of some of these theorems, in that they relate the solvability of the...
. The Dirichlet divisor problem, for which he found the first results, is still an unsolved problem in number theory despite later contributions by other researchers.
Analysis
Inspired by the work of his mentor in Paris, Dirichlet published in 1829 a famous memoir giving the conditionsDirichlet conditions
In mathematics, the Dirichlet conditions are sufficient conditions for a real-valued, periodic function f to be equal to the sum of its Fourier series at each point where f is continuous. Moreover, the behavior of the Fourier series at points of discontinuity is determined as well...
, showing for which functions the convergence of the Fourier series
Fourier series
In mathematics, a Fourier series decomposes periodic functions or periodic signals into the sum of a set of simple oscillating functions, namely sines and cosines...
holds. Before Dirichlet's solution, not only Fourier, but also Poisson and Cauchy had tried unsuccessfully to find a rigorous proof of convergence. The memoir pointed out Cauchy's mistake and introduced Dirichlet's test
Dirichlet's test
In mathematics, Dirichlet's test is a method of testing for the convergence of a series. It is named after mathematician Johann Dirichlet who published it in the Journal de Mathématiques Pures et Appliquées in 1862.- Statement :...
for the convergence of series. It also introduced the Dirichlet function as an example that not any function is integrable (the definite integral was still a developing topic at the time) and, in the proof of the theorem for the Forier series, introduced the Dirichlet kernel and the Dirichlet integral
Dirichlet integral
In mathematics, there are several integrals known as the Dirichlet integral, after the German mathematician Peter Gustav Lejeune Dirichlet.One of those isThis can be derived from attempts to evaluate a double improper integral two different ways...
.
Dirichlet also studied the first boundary value problem
Boundary value problem
In mathematics, in the field of differential equations, a boundary value problem is a differential equation together with a set of additional restraints, called the boundary conditions...
, for the Laplace equation, proving the unicity of the solution; this type of problem in the theory of partial differential equation
Partial differential equation
In mathematics, partial differential equations are a type of differential equation, i.e., a relation involving an unknown function of several independent variables and their partial derivatives with respect to those variables...
s was later named the Dirichlet problem
Dirichlet problem
In mathematics, a Dirichlet problem is the problem of finding a function which solves a specified partial differential equation in the interior of a given region that takes prescribed values on the boundary of the region....
after him. In the proof he notably used the principle that the solution is the function that minimizes the so-called Dirichlet energy. Riemann later named this approach the Dirichlet principle, although he knew it had also been used by Gauss and by Lord Kelvin
William Thomson, 1st Baron Kelvin
William Thomson, 1st Baron Kelvin OM, GCVO, PC, PRS, PRSE, was a mathematical physicist and engineer. At the University of Glasgow he did important work in the mathematical analysis of electricity and formulation of the first and second laws of thermodynamics, and did much to unify the emerging...
.
Definition of function
While trying to gauge the range of functions for which convergence of the Fourier series can be shown, Dirichlet defines a functionFunction (mathematics)
In mathematics, a function associates one quantity, the argument of the function, also known as the input, with another quantity, the value of the function, also known as the output. A function assigns exactly one output to each input. The argument and the value may be real numbers, but they can...
by the property that "to any x there corresponds a single finite y", but then restricts his attention to piecewise continuous functions. Based on this, he is credited with introducing the modern concept for a function, as opposed to the older vague understanding of a function as an analytic formula. Imre Lakatos
Imre Lakatos
Imre Lakatos was a Hungarian philosopher of mathematics and science, known for his thesis of the fallibility of mathematics and its 'methodology of proofs and refutations' in its pre-axiomatic stages of development, and also for introducing the concept of the 'research programme' in his...
cites Hermann Hankel
Hermann Hankel
Hermann Hankel was a German mathematician who was born in Halle, Germany and died in Schramberg , Imperial Germany....
as the early origin of this attribution, but disputes the claim saying that "there is ample evidence that he had no idea of this concept [...] for instance, when he discusses piecewise continuous functions, he says that at points of discontinuity the function has two values".
Other fields
Dirichlet also worked in mathematical physicsMathematical physics
Mathematical physics refers to development of mathematical methods for application to problems in physics. The Journal of Mathematical Physics defines this area as: "the application of mathematics to problems in physics and the development of mathematical methods suitable for such applications and...
, lecturing and publishing research in potential theory
Potential theory
In mathematics and mathematical physics, potential theory may be defined as the study of harmonic functions.- Definition and comments :The term "potential theory" was coined in 19th-century physics, when it was realized that the fundamental forces of nature could be modeled using potentials which...
(including the Dirichlet problem and Dirichlet priciple mentioned above), the theory of heat
Theory of heat
In the history of science, the theory of heat or mechanical theory of heat was a theory, introduced predominantly in 1824 by the French physicist Sadi Carnot, that heat and mechanical work are equivalent. It is related to the mechanical equivalent of heat...
and hydrodynamics. He improved on Lagrange
Lagrange
La Grange literally means the barn in French. Lagrange may refer to:- People :* Charles Varlet de La Grange , French actor* Georges Lagrange , translator to and writer in Esperanto...
's work on conservative systems by showing that the condition for equilibrium
Mechanical equilibrium
A standard definition of static equilibrium is:This is a strict definition, and often the term "static equilibrium" is used in a more relaxed manner interchangeably with "mechanical equilibrium", as defined next....
is that the potential energy
Potential energy
In physics, potential energy is the energy stored in a body or in a system due to its position in a force field or due to its configuration. The SI unit of measure for energy and work is the Joule...
is minimal.
Although he didn't publish much in the field, Dirichlet lectured on probability theory
Probability theory
Probability theory is the branch of mathematics concerned with analysis of random phenomena. The central objects of probability theory are random variables, stochastic processes, and events: mathematical abstractions of non-deterministic events or measured quantities that may either be single...
and least squares
Least squares
The method of least squares is a standard approach to the approximate solution of overdetermined systems, i.e., sets of equations in which there are more equations than unknowns. "Least squares" means that the overall solution minimizes the sum of the squares of the errors made in solving every...
, introducing some original methods and results, in particular for limit theorems
Asymptotic theory (statistics)
In statistics, asymptotic theory, or large sample theory, is a generic framework for assessment of properties of estimators and statistical tests...
and an improvement of Laplace's method of approximation related to the central limit theorem
Central limit theorem
In probability theory, the central limit theorem states conditions under which the mean of a sufficiently large number of independent random variables, each with finite mean and variance, will be approximately normally distributed. The central limit theorem has a number of variants. In its common...
. The Dirichlet distribution and the Dirichlet process
Dirichlet process
In probability theory, a Dirichlet process is a stochastic process that can be thought of as a probability distribution whose domain is itself a random distribution...
, based on the Dirichlet integral, are named after him.
Honours
Dirichlet was elected as a member of several academies:- Prussian Academy of SciencesPrussian Academy of SciencesThe Prussian Academy of Sciences was an academy established in Berlin on 11 July 1700, four years after the Akademie der Künste or "Arts Academy", to which "Berlin Academy" may also refer.-Origins:...
(1832) - Saint Petersburg Academy of SciencesRussian Academy of SciencesThe Russian Academy of Sciences consists of the national academy of Russia and a network of scientific research institutes from across the Russian Federation as well as auxiliary scientific and social units like libraries, publishers and hospitals....
(1833) - corresponding member - Göttingen Academy of SciencesGöttingen Academy of SciencesThe Göttingen Academy of Sciences is the second oldest of the seven academies of sciences in Germany. It has the task of promoting research under its own auspices and in collaboration with academics in and outside Germany...
(1846) - French Academy of SciencesFrench Academy of SciencesThe French Academy of Sciences is a learned society, founded in 1666 by Louis XIV at the suggestion of Jean-Baptiste Colbert, to encourage and protect the spirit of French scientific research...
(1854) - foreign member - Royal Swedish Academy of SciencesRoyal Swedish Academy of SciencesThe Royal Swedish Academy of Sciences or Kungliga Vetenskapsakademien is one of the Royal Academies of Sweden. The Academy is an independent, non-governmental scientific organization which acts to promote the sciences, primarily the natural sciences and mathematics.The Academy was founded on 2...
(1854) - Royal Belgian Academy of SciencesThe Royal Academies for Science and the Arts of BelgiumThere are two Royal Academies for Science and the Arts in Belgium, corresponding to the two main languages of the country, Dutch and French . The Academies are located in the Palace of Academies in Brussels....
(1855) - Royal SocietyRoyal SocietyThe Royal Society of London for Improving Natural Knowledge, known simply as the Royal Society, is a learned society for science, and is possibly the oldest such society in existence. Founded in November 1660, it was granted a Royal Charter by King Charles II as the "Royal Society of London"...
(1855) - foreign member
In 1855 Dirichlet was awarded the civil class medal of the Pour le Mérite
Pour le Mérite
The Pour le Mérite, known informally as the Blue Max , was the Kingdom of Prussia's highest military order for German soldiers until the end of World War I....
order at von Humboldt's recommendation. The Dirichlet crater
Dirichlet (crater)
Dirichlet is a lunar impact crater that is located on the Moon's far side. It is attached to the southern outer rim of the crater Henry. To the south-southeast is the much larger crater Tsander....
on the Moon
Moon
The Moon is Earth's only known natural satellite,There are a number of near-Earth asteroids including 3753 Cruithne that are co-orbital with Earth: their orbits bring them close to Earth for periods of time but then alter in the long term . These are quasi-satellites and not true moons. For more...
and the 11665 Dirichlet
11665 Dirichlet
11665 Dirichlet is an outer main-belt asteroid discovered on April 14, 1997 by Paul G. Comba at Prescott. It is one of very few asteroids located in the 2 : 1 mean motion resonance with Jupiter.- External links :*...
asteroid are named after him.

